高中数学选修2-1公开课课件2_3_2双曲线的简单几何性质(一)

高中数学选修2-1公开课课件2_3_2双曲线的简单几何性质(一)

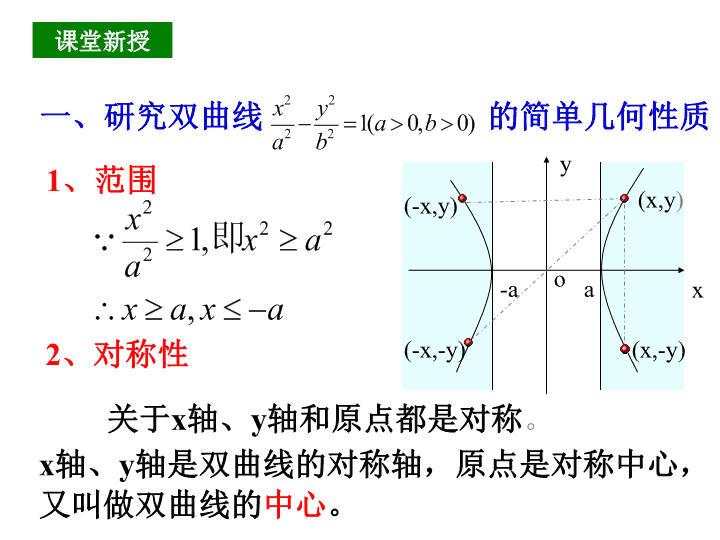
双曲线的性质 ( 一 ) 定义 图象 方程 焦点 a.b.c 的关系 | |MF 1 | - |MF 2 | | =2 a （０ < 2 a <|F 1 F 2 | ） F ( ±c, 0) 　 F(0, ± c) 2 、对称性 一、研究双曲线 的简单几何性质 1 、范围 关于 x 轴、 y 轴和原点都是对称 。 x 轴、 y 轴是双曲线的对称轴，原点是对称中心， 又叫做双曲线的 中心 。 x y o -a a (-x,-y) (-x,y) (x,y ) (x,-y) 课堂新授 3 、顶点 （ 1 ）双曲线与对称轴的交点，叫做双曲线的 顶点 x y o -b b -a a 如图，线段 叫做双曲线的实轴，它的长为 2a,a 叫做实半轴长；线段 叫做双曲线的虚轴，它的长为 2b,b 叫做双曲线的虚半轴长 （ 2 ） 实轴与虚轴等长的双曲线 叫 等轴双曲线 （ 3 ） M(x,y) 4 、渐近线 N(x,y’) Q 慢慢靠近 x y o a b （ 1 ） （ 2 ） 利用渐近线可以较准确的 画出双曲线的草图 （ 3 ） 动画演示 5 、离心率 离心率 。 c>a>0 e >1 e 是表示双曲线开口大小的一个量 ,e 越大开口越大 （ 1 ）定义： （ 2 ） e 的范围 ： （ 3 ） e 的含义： （ 4 ） 等轴双曲线的离心率 e= ? ( 5 ) x y o -a a b -b （ 1 ）范围 : （ 2 ）对称性 : 关于 x 轴、 y 轴、原点都对称 （ 3 ）顶点 : (0,-a) 、 (0,a) （ 4 ）渐近线 : （ 5 ）离心率 : 小 结 或 或 关于坐标 轴和 原点 都对 称 性质 双曲线 范围 对称 性 顶点 渐近 线 离心 率 图象 例 1 : 求双曲线 的实半轴长 , 虚半轴长 , 焦点坐标 , 离心率 . 渐近线方程。 解：把方程化为标准方程 可得 : 实半轴长 a=4 虚半轴长 b=3 半焦距 c= 焦点坐标是 (0,-5),(0,5) 离心率 : 渐近线方程 : 144 16 9 2 2 = - x y 1 3 4 2 2 2 2 = - x y 5 3 4 2 2 = + 4 5 = = a c e 例题讲解 例 2 1 、若双曲线的渐近线方程为 则双曲线的离心率为 。 2 、若双曲线的离心率为 2 ，则两条渐近线的夹角为 。 课堂练习 例 3 : 求下列双曲线的标准方程： 例题讲解 法二： 巧设方程 , 运用待定系数法 . ⑴ 设双曲线方程为 , 法二： 设双曲线方程为 ∴ 双曲线方程为 ∴ , 解之得 k =4, 1 、“共渐近线”的双曲线的应用 λ>0 表示焦点在 x 轴上的双曲线； λ<0 表示焦点在 y 轴上的双曲线。 4. 求与椭圆 有共同焦点，渐近线方程为 的双曲线方程。 解： 椭圆的焦点在 x 轴上，且坐标为 双曲线的渐近线方程为 解出 1 2 = + b y a x 2 2 2 （ a ＞ b ＞ 0 ） 1 2 2 2 2 = - b y a x ( a ＞ 0 b ＞ 0) 2 2 2 = + b a (a ＞ 0 b ＞ 0) c 2 2 2 = - b a (a ＞ b ＞ 0) c 椭 圆 双曲线 方程 a b c 关系 图象 椭圆与双曲线的比较 y X F 1 0 F 2 M X Y 0 F 1 F 2 p 小 结 渐近线 离心率 顶点 对称性 范围 准线 |x|  a,|y|≤b |x| ≥ a ， y R 对称轴： x 轴， y 轴 对称中心：原点 对称轴： x 轴， y 轴 对称中心：原点 （ -a,0) (a,0) (0,b) (0,-b) 长轴： 2a 短轴： 2b (-a,0) (a,0) 实轴： 2a 虚轴： 2b e = a c ( 0 ＜ e ＜ 1 ) a c e= (e 1) 无 y = a b x ±