- 2021-04-13 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2019届浙江省名校协作体高二上学期月考数学试卷(解析版)
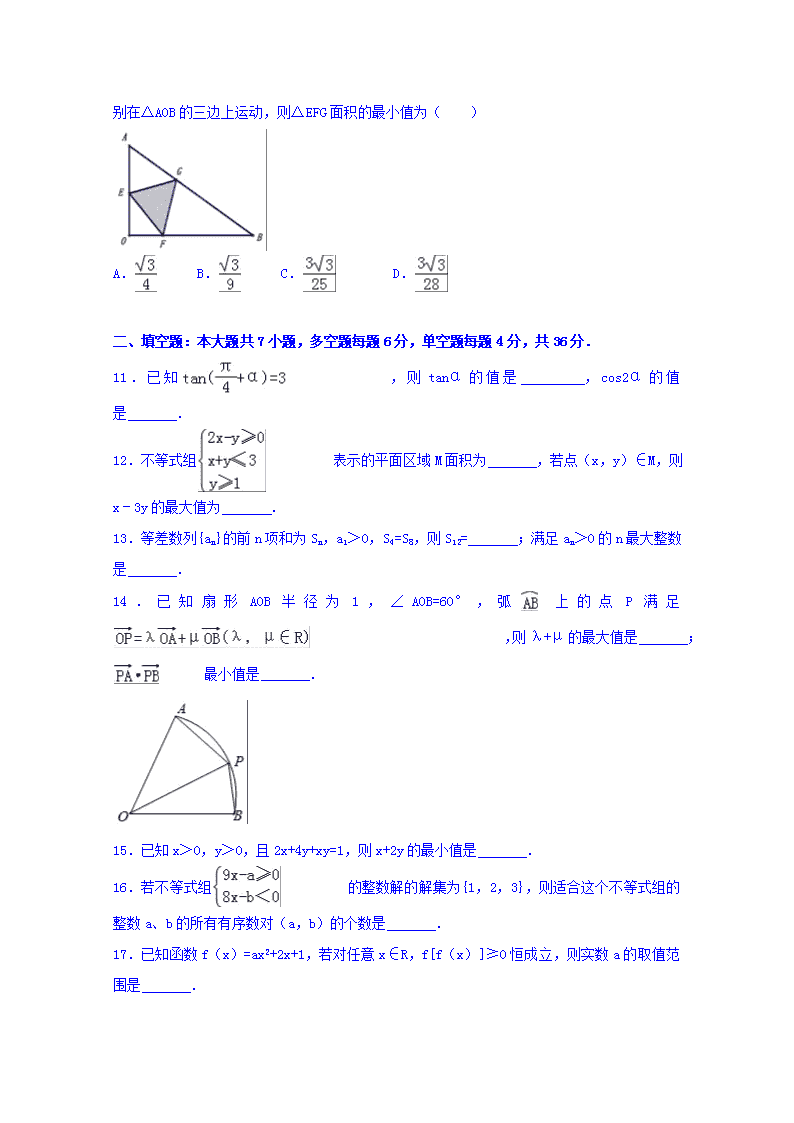
全*品*高*考*网, 用后离不了!2017-2018学年浙江省名校协作体高二(上)月考数学试卷 一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数的定义域为( ) A.(﹣∞,0] B.(﹣∞,0) C.[0,+∞) D.(0,+∞) 2.下列函数既是奇函数,又在(0,+∞)上为增函数的是( ) A. B.y=|x| C. D.y=lg(x+1) 3.等比数列{an}的公比为q,成等差数列,则q值为( ) A. B. C.或 D.1或 4.计算:(log43+log83)(log32+log92)=( ) A. B. C.5 D.15 5.的值域为[0,+∞),则a的取值范围是( ) A.(2,+∞) B.(﹣∞,﹣1)∪(2,+∞) C.[﹣1,2] D.[0,2] 6.为得到函数y=sin(x+)的图象,可将函数y=sinx的图象向左平移m个单位长度,或向右平移n个单位长度(m,n均为正数),则|m﹣n|的最小值是( ) A. B. C. D. 7.以方程x2+px+1=0的两根为三角形两边之长,第三边长为2,则实数p的取值范围是( ) A.p<﹣2 B.p≤﹣2或p≥2 C. D. 8.已知坐标平面上的凸四边形ABCD满足,那么的取值范围是( ) A.(﹣1,) B.(﹣1,2] C.[﹣2,0) D.[0,2] 9.函数f(x)=,则函数h(x)=f(x)﹣log4x的零点个数为( ) A.2个 B.3个 C.4个 D.5个 10.如图,在△AOB中,∠AOB=90°,,等边△ EFG三个顶点分别在△AOB的三边上运动,则△EFG面积的最小值为( ) A. B. C. D. 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.已知,则tanα的值是 ,cos2α的值是 . 12.不等式组表示的平面区域M面积为 ,若点(x,y)∈M,则x﹣3y的最大值为 . 13.等差数列{an}的前n项和为Sn,a1>0,S4=S8,则S12= ;满足an>0的n最大整数是 . 14.已知扇形AOB半径为1,∠AOB=60°,弧上的点P满足,则λ+μ的最大值是 ;最小值是 . 15.已知x>0,y>0,且2x+4y+xy=1,则x+2y的最小值是 . 16.若不等式组的整数解的解集为{1,2,3},则适合这个不等式组的整数a、b的所有有序数对(a,b)的个数是 . 17.已知函数f(x)=ax2+2x+1,若对任意x∈R,f[f(x)]≥0恒成立,则实数a的取值范围是 . 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.已知函数, (I)求f(x)的最大值和对称中心坐标; (Ⅱ)讨论f(x)在[0,π]上的单调性. 19.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知sinA=. (Ⅰ)若a2﹣c2=b2﹣mbc,求实数m的值; (Ⅱ)若a=,求△ABC面积的最大值. 20.数列{an}满足:. (Ⅰ)求a3,a4,并证明数列{a2n+1}是等比数列; (Ⅱ)求数列{an}前2n项和S2n. 21.已知f(x)=ax2+bx+c(a,b∈R,a≠0). (I)当a=1,b=2时,若存在实数x1,x2(x1≠x2)使得|f(xi)|=2(i=1,2),求实数c的取值范围; (II)若a>0,函数f(x)在[﹣5,﹣2]上不单调,且它的图象与x轴相切,记f(2)=λ(b﹣2a),求实数λ的取值范围. 22.已知函数. (Ⅰ)当a=﹣1,b=﹣2时,求证:f(x)在(0,2)上是减函数; (Ⅱ)若对任意的实数a,都存在x∈[1,2],使得|f(x)|≤1成立,求实数b的取值范围. 2017-2018学年浙江省名校协作体高二(上)月考数学试卷 参考答案与试题解析 一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数的定义域为( ) A.(﹣∞,0] B.(﹣∞,0) C.[0,+∞) D.(0,+∞) 【考点】33:函数的定义域及其求法. 【分析】由根式内部的代数式大于等于0,求解不等式即可得答案. 【解答】解:由, 得,解得x≤0. ∴函数的定义域为(﹣∞,0]. 故选:A. 2.下列函数既是奇函数,又在(0,+∞)上为增函数的是( ) A. B.y=|x| C. D.y=lg(x+1) 【考点】3K:函数奇偶性的判断;3E:函数单调性的判断与证明. 【分析】根据题意,依次分析选项中函数的奇偶性与单调性,综合即可得答案. 【解答】解:根据题意,依次分析选项: 对于A、y=为奇函数,但在区间(0,+∞)上为减函数,不符合题意; 对于B、y=|x|,有f(﹣x)=|﹣x|=|x|=f(x),即f(x)为偶函数,不符合题意; 对于C、y=2x﹣()x,有f(﹣x)=2(﹣x)﹣()(﹣x)=﹣[2x﹣()x]=﹣f(x),即函数f(x)为奇函数, 在(0,+∞)上,函数y=2x为增函数,y=()x为减函数,则函数f(x)在(0,+∞)上为增函数,符合题意; 对于D、y=lg(x+1),为非奇非偶函数,不符合题意; 故选:C. 3.等比数列{an}的公比为q,成等差数列,则q值为( ) A. B. C.或 D.1或 【考点】8M:等差数列与等比数列的综合. 【分析】运用等差数列的中项的性质和等比数列的通项公式,解方程即可得到所求公比的值. 【解答】解:等比数列{an}的公比为q,成等差数列, 可得2a2=a1+a3, 即有2a1q=a1+a1q2, 化为q2﹣4q+2=0, 解得q=2±, 故选:C. 4.计算:(log43+log83)(log32+log92)=( ) A. B. C.5 D.15 【考点】4H:对数的运算性质. 【分析】化简(log43+log83)(log32+log92)=(log23+log23)(log32+log32),且log23•log32=1,从而解得. 【解答】解:(log43+log83)(log32+log92) =(log23+log23)(log32+log32) =log23•log32 =; 故选:A. 5.的值域为[0,+∞),则a的取值范围是( ) A.(2,+∞) B.(﹣∞,﹣1)∪(2,+∞) C.[﹣1,2] D.[0,2] 【考点】34:函数的值域. 【分析】令t=2ax2+4x+a﹣1,则y=,由函数y的值域为[0,+∞),则函数t的值域为[0,+∞),然后分类讨论,当a=0时,函数t的值域为[0,+∞),当a≠0时,要使函数t=2ax2+4x+a﹣1的值域为[0,+∞),则,求解即可得a的取值范围. 【解答】解:令t=2ax2+4x+a﹣1,则y=, ∵函数的值域为[0,+∞), ∴函数t=2ax2+4x+a﹣1的值域为[0,+∞), 当a=0时,t=4x﹣1, 由4x﹣1≥0,得函数t=4x﹣1的值域为[0,+∞), 当a≠0时,要使函数t=2ax2+4x+a﹣1的值域为[0,+∞), 则,即, 解得0<a≤2, ∴a的取值范围是[0,2]. 故选:D. 6.为得到函数y=sin(x+)的图象,可将函数y=sinx的图象向左平移m个单位长度,或向右平移n个单位长度(m,n均为正数),则|m﹣n|的最小值是( ) A. B. C. D. 【考点】HJ:函数y=Asin(ωx+φ)的图象变换. 【分析】依题意得m=2k1π+,n=2k2π+(k1、k2∈N),于是有|m﹣n|=|2(k1﹣k2)π﹣|,从而可求得|m﹣n|的最小值. 【解答】解:由条件可得m=2k1π+,n=2k2π+(k1、k2∈N), 则|m﹣n|=|2(k1﹣k2)π﹣|, 易知(k1﹣k2)=1时, |m﹣n|min=. 故选:B. 7.以方程x2+px+1=0的两根为三角形两边之长,第三边长为2,则实数p的取值范围是( ) A.p<﹣2 B.p≤﹣2或p≥2 C. D. 【考点】HT:三角形中的几何计算. 【分析】先根据方程有两个实数根求出p的取值范围,再根据韦达定理求出x1+x2及x1x2的值,根据三角形的三边关系即可得出结论. 【解答】解:∵三角形的两边长是方程x2+px+1=0的两个根, ∴△≥0,即△=p2﹣4≥0,解得p≥2或p≤﹣2. ∵x1+x2=﹣p>2,x1x2=1,|x1﹣x2|<2, 故p<﹣2,p2<8, ∴﹣2<p<﹣2, 故选:D. 8.已知坐标平面上的凸四边形ABCD满足,那么的取值范围是( ) A.(﹣1,) B.(﹣1,2] C.[﹣2,0) D.[0,2] 【考点】9R:平面向量数量积的运算. 【分析】根据向量的模的计算和向量的坐标运算得到四边形ABCD为对角线垂直且相等的四边形,问题得以解决. 【解答】解:∵, ∴•=1×(﹣)+×1=0, ∴⊥, ∴凸四边形ABCD的面积为AC×BD=×2×2=2, 设AC与BD交点为O,OC=x,OD=y,则AO=2﹣x,BO=2﹣y, 则•=(+)(+)=•+•+•+•2﹣=x(x﹣2)+y(y﹣2)=(x﹣1)2+(y﹣1)2﹣2,(0<x,y<2); ∴当x=y=1时, •=﹣2为最小值, 当x→0或1,y→0或1时, •接近最大值0, ∴•的取值范围是[﹣2,0). 故选:C. 9.函数f(x)=,则函数h(x)=f(x)﹣log4x的零点个数为( ) A.2个 B.3个 C.4个 D.5个 【考点】52:函数零点的判定定理. 【分析】函数h(x)=f(x)﹣log4x的零点个数⇔函数f(x)与函数y=log4x的图象交点个数. 画出函数f(x)与函数y=log4x的图象(如图),根据图象可得答案. 【解答】解:函数h(x)=f(x)﹣log4x的零点个数⇔函数f(x)与函数y=log4x的图象交点个数. 画出函数f(x)与函数y=log4x的图象(如图), 根据图象可得函数f(x)与函数y=log4x的图象交点为5个. ∴函数h(x)=f(x)﹣log4x的零点个数为5个. 故选:D 10.如图,在△AOB中,∠AOB=90°,,等边△EFG三个顶点分别在△AOB的三边上运动,则△EFG面积的最小值为( ) A. B. C. D. 【考点】3H:函数的最值及其几何意义. 【分析】设等边三角形的边长为t,结合几何关系得到面积函数,结合三角函数的性质即可求得面积的最小值. 【解答】解:设△EFG的边长为t,∠OEF=θ,则∠AGE=θ,∠EAO=60°, OE=tcosθ,,∴, 所以, 且:, 其中, 当sin(θ+φ)=1 时,△EFG取得面积的最小值. 故选:D. 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.已知,则tanα的值是 ,cos2α的值是 . 【考点】GR:两角和与差的正切函数;GT:二倍角的余弦. 【分析】由两角和与差的正切函数展开已知等式,整理即可求得tanα的值,由万能公式即可求得cos2α的值. 【解答】解:∵tan(+α)==3, 解得:tanα=, ∴cos2α==. 故答案为:,. 12.不等式组表示的平面区域M面积为 ,若点(x,y)∈M,则x﹣3y的最大值为 ﹣1 . 【考点】7C:简单线性规划. 【分析】由约束条件作出可行域,联立方程组求出三角形顶点坐标,则面积可求;令z=x﹣3y,化为y=,数形结合得到最优解,把最优解的坐标代入得答案. 【解答】解:由约束条件作出可行域如图: 联立,解得A(); 联立,解得B(2,1); 联立,解得C(1,2). ∴平面区域M面积为S=; 令z=x﹣3y,化为y=,由图可知,当直线y=过B时,直线在y轴上的截距最小,z有最大值﹣1. 故答案为:,﹣1. 13.等差数列{an}的前n项和为Sn,a1>0,S4=S8,则S12= 0 ;满足an>0的n最大整数是 6 . 【考点】8F:等差数列的性质. 【分析】根据等差数列{an}性质可知a5+a7+a6+a8=0,即4a5+6d=0,从而有4a1+22d=0.即可求出S12,求解通项,令通项公式等于0,即可求解n的最大整数. 【解答】解:由题意,{an}是等差数列,S4=S8, 可得:a5+a7+a6+a8=0, 即4a5+6d=0, 从而有4a1+22d=0. ∴a1=﹣5.5d. 那么:S12===0. 通项an=a1+(n﹣1)d=﹣6.5d+nd. 令an=0,可得n=6.5, ∵k∈N*. ∴n最大整数为6. 故答案为:0,6. 14.已知扇形AOB半径为1,∠AOB=60°,弧上的点P满足,则λ+μ的最大值是 ;最小值是 ﹣ . 【考点】9R:平面向量数量积的运算;9V:向量在几何中的应用. 【分析】建立坐标系,设∠BOP=θ,用θ表示出P点坐标,得出λ+μ及关于θ的表达式,根据θ的范围和三角函数的性质得出答案. 【解答】解:以O为原点,以OB为x轴建立平面直角坐标系, 设∠BOP=θ,则P(cosθ,sinθ),B(1,0),A(,), ∵, ∴,即. ∴λ+μ=cosθ+sinθ=sin(θ+), ∵P在上,∴0, ∴当时,λ+μ取得最大值. =(,﹣sinθ),=(1﹣cosθ,﹣sinθ), ∴=()(1﹣cosθ)+(﹣sinθ)(﹣sinθ)=﹣cosθ﹣sinθ=﹣sin(θ+). ∵0≤θ≤,∴≤≤. ∴当=时,取得最小值﹣. 故答案为:, . 15.已知x>0,y>0,且2x+4y+xy=1,则x+2y的最小值是 2﹣4 . 【考点】7G:基本不等式在最值问题中的应用. 【分析】令t=x+2y,利用基本不等式化简已知条件,转化求解最小值. 【解答】解:令t=x+2y,则2x+4y+xy=1,化为:1=2x+4y+xy≤2(x+2y)+()2=2t+, 因为x>0,y>0,所以x+2y>0,即t>0,t2+16t﹣8≥0,解得t≥2﹣4. x+2y的最小值是2﹣4. 故答案为:2﹣4. 16.若不等式组的整数解的解集为{1,2,3},则适合这个不等式组的整数a、b的所有有序数对(a,b)的个数是 72 . 【考点】7E:其他不等式的解法. 【分析】由题意可得满足不等式≤x<的整数x共有3个,分别为1、2、3,可得0≤<1,3<≤4,故整数a共有9个,整数b共有8个,由此可得有序数对(a,b)的个数. 【解答】解:若不等式组的整数解的解集为{1,2,3},即满足不等式≤x<的整数x共有3个,分别为1、2、3, 可得0≤<1,3<≤4,故整数a共有9个,整数b共有8个, 则适合这个不等式组的整数a、b的所有有序数对(a,b)的个数为9×8=72( 个), 故答案为:72. 17.已知函数f(x)=ax2+2x+1,若对任意x∈R,f[f(x)]≥0恒成立,则实数a的取值范围是 a≥ . 【考点】3W:二次函数的性质. 【分析】根据二次函数的图象和性质,分当a=0时,当a>0时和当a<0时,分类讨论满足条件的实数a的取值范围,综合可得答案. 【解答】解:当a=0时,函数f(x)=2x+1,f[f(x)]=4x+3, 不满足对任意x∈R,f[f(x)]≥0恒成立, 当a>0时,f(x)≥=1﹣, f[f(x)]≥f(1﹣)=a(1﹣)2+2(1﹣)+1=a﹣+1, 解a﹣+1≥0得:a≤,或a≥, 故a≥, 当a<0时,f(x)≤=1﹣, 不满足对任意x∈R,f[f(x)]≥0恒成立, 综上可得:a≥ 故答案为:a≥ 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.已知函数, (I)求f(x)的最大值和对称中心坐标; (Ⅱ)讨论f(x)在[0,π]上的单调性. 【考点】HW:三角函数的最值;H5:正弦函数的单调性;H6:正弦函数的对称性. 【分析】(Ⅰ)首先通过三角函数关系式的恒等变换,把函数关系式变形成正弦型函数,进一步利用整体思想求出函数的最值和对称中心. (Ⅱ)根据(Ⅰ)所求的关系式,利用整体思想求出函数的单调递增区间和递减区间. 【解答】解:(Ⅰ), =, =, 则:的最大值为2, 令:(k∈Z), 解得:(k∈Z), 则函数f(x)对称中心为:; (Ⅱ)由(Ⅰ)得: 令:,(k∈Z), 解得:(k∈Z), 当k=0或1时,得到函数f(x)的单调递增区间为:和; 同理:令:(k∈Z), 解得:,(k∈Z), 当k=0时得到函数f(x)的单调递减区间为:. 19.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知sinA=. (Ⅰ)若a2﹣c2=b2﹣mbc,求实数m的值; (Ⅱ)若a=,求△ABC面积的最大值. 【考点】HR:余弦定理;%H:三角形的面积公式. 【分析】(Ⅰ)已知等式两边平方后整理可解得cosA=,而由已知及余弦定理可得=,从而解得m的值. (Ⅱ)由(Ⅰ)可求得sinA=,结合余弦定理可求得bc≤a2 ,即可由三角形面积公式求最大值. 【解答】解:(Ⅰ)由sinA=两边平方可得:2sin2A=3cosA, 即(2cosA﹣1)(cosA+2)=0,解得:cosA=…4分 而a2﹣c2=b2﹣mbc可以变形为: =, 即cosA==,所以m=1…7分 (Ⅱ)由(Ⅰ)知cosA=,则sinA=,又=…9分 所以bc=b2+c2﹣a2≥2bc﹣a2,即bc≤a2…12分 故S△ABC=bcsinA≤=…15分 20.数列{an}满足:. (Ⅰ)求a3,a4,并证明数列{a2n+1}是等比数列; (Ⅱ)求数列{an}前2n项和S2n. 【考点】8H:数列递推式;8E:数列的求和. 【分析】(Ⅰ)代入递推关系可得a3,a4.n=2k,a2k+2=3a2k+2,(k=1,2,3,…).变形为a2k+2+1=3(a2k+1),即可证明. (Ⅱ){an}的通项公式,分组求和,利用等差数列与等比数列的求和公式即可得出. 【解答】解:(Ⅰ)a3=3,a4=8 当n=2k,a2k+2=3a2k+2,(k=1,2,3,…). 变形为a2k+2+1=3(a2k+1),(k=1,2,3,…). ∴数列{a2n+1}是等比数列. (Ⅱ){an}的通项公式, , , . 21.已知f(x)=ax2+bx+c(a,b∈R,a≠0). (I)当a=1,b=2时,若存在实数x1,x2(x1≠x2)使得|f(xi)|=2(i=1,2),求实数c的取值范围; (II)若a>0,函数f(x)在[﹣5,﹣2]上不单调,且它的图象与x轴相切,记f(2)=λ(b﹣2a),求实数λ的取值范围. 【考点】3W:二次函数的性质;3E:函数单调性的判断与证明. 【分析】(Ⅰ)根据二次函数的性质得到关于c的不等式组,解出即可; (Ⅱ)由f(2)=λ(b﹣2a),表示出λ,结合二次函数的性质求出λ的范围即可. 【解答】解:(Ⅰ)由题意可得: 方程x2+2x+c=2有两个不等的根, 且x2+2x+c=﹣2无根, 所以可得; (Ⅱ)由a>0,函数f(x)在[﹣5,﹣2]上不单调, 且它的图象与x轴相切, 可得,即, 由f(2)=λ(b﹣2a), 得, 令,∴2<t<8, 且 =. 22.已知函数. (Ⅰ)当a=﹣1,b=﹣2时,求证:f(x)在(0,2)上是减函数; (Ⅱ)若对任意的实数a,都存在x∈[1,2],使得|f(x)|≤1成立,求实数b的取值范围. 【考点】3R:函数恒成立问题;3E:函数单调性的判断与证明. 【分析】(Ⅰ)根据定义即可证明, (Ⅱ)对任意的实数a,存在x∈[1,2],使得|f(x)|≤1成立⇔对任意的实数a,存在x∈[1,2],使得成立⇔,分别构造函数,分类讨论即可求出. 【解答】解:(Ⅰ)设任意x1,x2∈(0,2)且x1<x2,, , ∴任意x1,x2∈(0,2)且x1<x2时,f(x1)>f(x2),故f(x)在(0,2)上是减函数,得证. (Ⅱ) 对任意的实数a,存在x∈[1,2],使得|f(x)|≤1成立⇔对任意的实数a,存在x∈[1,2],使得成立⇔. 设, ①当b≤0时,,则 ②当时,,则 ③当时,,则 ④当时,,则 综上,所求实数b的范围是b≤﹣2或b≥6 查看更多