- 2021-04-13 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
宁夏贺兰县景博中学2019-2020学年高二上学期月考数学(文)试题
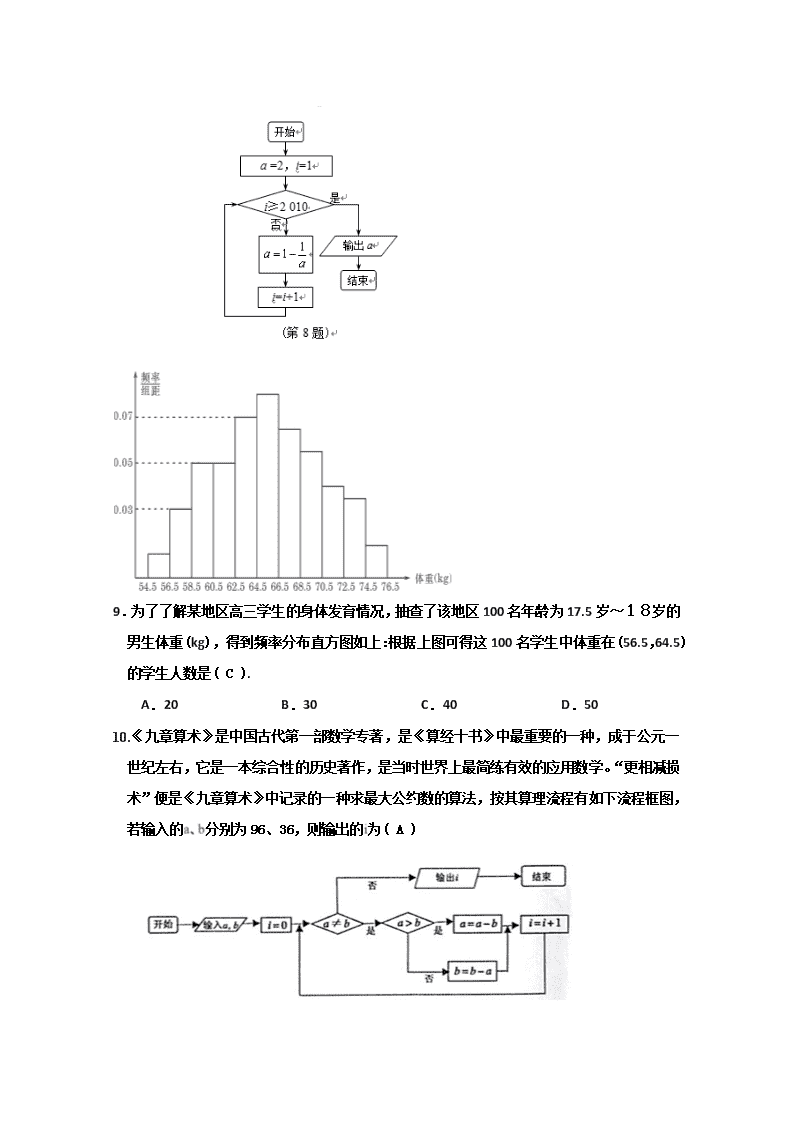
景博高中2019-2020学年第一学期高二年级第二次月考 数学(文科) 一、选择题(每小题5分,共60分) 1.“关于x的不等式f(x)>0有解”等价于( A ) A.∃x0∈R,使得f(x0)>0成立 B.∃x0∈R,使得f(x0)≤0成立 C.∀x∈R,使得f(x)>0成立 D.∀x∈R,f(x)≤0成立 2.已知命题p:∀x>0,总有(x+1)ex>1,则﹁p为(B ) A.∃x0≤0,使得(x0+1)e≤1 B.∃x0>0,使得(x0+1)e≤1 C.∀x>0,总有(x+1)ex≤1 D.∀x≤0,使得(x+1)ex≤1 3、已知双曲线-=1(a>0)的离心率为2,则a=( D ) A.2 B. C. D.1 4、椭圆的离心率为( D ) A. B. C. D. 5用系统抽样法(按等距离的规则)要从160名学生中抽取容量为20的样本,将160名学生从1~160编号.按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组应抽出的号码为125,则第一组中按此抽签方法确定的号码是( B ) A.7 B.5 C.4 D.3 6.具有A、B、C三种性质的总体,其容量为63,将A、B、C三种性质的个体按1∶2∶4的比例进行分层抽样调查,如果抽取的样本容量为21,则A、B、C三种元素分别抽取( C ) A.12,6,3 B.12,3,6 C.3,6,12 D.3,12,6 7.工商局对超市某种食品抽查,这种食品每箱装有6袋,经检测 某箱中每袋的重量(单位:克)如以下茎叶图所示.则这箱食品 一袋的平均重量和重量的中位数分别为( B ) A.249,248 B.249,249 C.248,249 D.248,248 8.已知某程序框图如图所示,则执行该程序后输出的结果是( A ). A. B.1 C.2 D. 9.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如上:根据上图可得这100名学生中体重在(56.5,64.5)的学生人数是( C ). A.20 B.30 C.40 D.50 10.《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右,它是一本综合性的历史著作,是当时世界上最简练有效的应用数学。“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法,按其算理流程有如下流程框图,若输入的分别为96、36,则输出的为( A ) A. 4 B. 5 C. 6 D. 7 11.函数f(x)=在区间[a-1,a+1]上单调递减,则实数a的取值范围是( A ) A.(1,2] B.[4,+∞) C.(-∞,2] D.(0,3] 12.下列命题正确的个数是( A ) (1)已知、,,则动点的轨迹是双曲线左边一支; (2)在平面直角坐标系内,到点(1,1)和直线x+2y=3的距离相等的点的轨迹是抛物线; (3)设定点,,动点满足条件,则点的轨迹是椭圆。 A.0 个 B.1个 C.2个 D.3个 二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.已知曲线上一点,则过点P的切线的倾斜角为____450______. 14.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7.现去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为____9.5_____,__0.016_____. 15函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为___(-1,+ ∞)___. 16. 若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-2的最小距离为___________. 三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17. (本小题10).若f(x)在[2,+)是增函数,求实数a的范围。 18. (本小题12)过抛物线y2=4x的焦点F的直线交y轴于点A,抛物线上有一点B满足=+(O为坐标原点),求△BOF的面积。 由题可知F(1,0),可设过焦点F的直线方程为y=k(x-1)(可知k存在),则A(0,-k),∴B(1,-k),由点B在抛物线上,得k2=4,k=±2,即B(1,±2), S△BOF=·|OF|·|yB|=×1×2=1. 答案:1 19.(本小题12)已知椭圆C:+=1(a>b>0)的离心率为,焦点与短轴的两顶点的连线 与圆x2+y2=相切.求椭圆C的方程; 解:(1)∵椭圆C:++=1(a>b>0)的离心率为,焦点与短轴的两顶点的连线与圆x2+y2=相切, ∴解得c2=1,a2=4,b2=3. ∴椭圆C的方程为+=1. 20. (本小题12)已知动圆过定点F(0,2),且与定直线L:y=-2相切. (1)求动圆圆心的轨迹C的方程; (2)若AB是轨迹C的动弦,且AB过F(0,2),分别以A、B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ. 解:(1)依题意,圆心的轨迹是以F(0,2)为焦点,L:y=-2为准线的抛物线. 因为抛物线焦点到准线距离等于4, 所以圆心的轨迹是x2=8y. (2)证明:因为直线AB与x轴不垂直, 设AB:y=kx+2. A(x1,y1),B(x2,y2). 由 可得x2-8kx-16=0,x1+x2=8k,x1x2=-16. 抛物线方程为y=x2,求导得y′=x. 所以过抛物线上A、B两点的切线斜率分别是k1=x1,k2=x2,k1k2=x1·x2=x1·x2=-1. 所以AQ⊥BQ. 21. (本小题12)已知函数在处有极值. (1)求的值和函数的单调区间; (2)求函数在区间上的最值.[来 (Ⅰ) 由题意; 所以:,定义域为 令,单增区间为; 令,单减区间为 (Ⅱ)由(1)知在区间函数单调递减,在区间函数单调递增, 所以,而,,所以。 源:学,科,网Z,X,X,K] 22. (本小题12)某市十所重点中学进行高三联考,共有5 000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表: 分组 频数 频率 [80,90) ① ② [90,100) 0.050 [100,110) 0.200 [110,120) 36 0.300 [120,130) 0.275 [130,140) 12 ③ [140,150) 0.050 合计 ④ (1)根据上面频率分布表,推出①,②,③,④处的数值分别为 , , , ; (2)在所给的坐标系中画出区间[80,150]上的频率分布直方图; (3)根据题中信息估计总体:(i)120分及以上的学生数; (ii)平均分;(iii)成绩落在[126,150]中的概率. (iii)成绩落在[126,150]中的概率为:P=×0.275+0.10+0.050=0.260. 解:(1)①,②,③,④处的数值分别为:3,0.025,0.100,1. (2)频率分布直方图如图所示 (3)(i)120分及以上的学生数为: (0.275+0.100+0.050)×5 000=2 125; (ii)平均分为:=85×0.025+95×0.050+105×0.200+115×0.300+125×0.275+135×0.100+145×0.050=117.5. (iii)成绩落在[126,150]中的概率为:P=×0.275+0.10+0.050=0.260.查看更多