全等三角形导学案

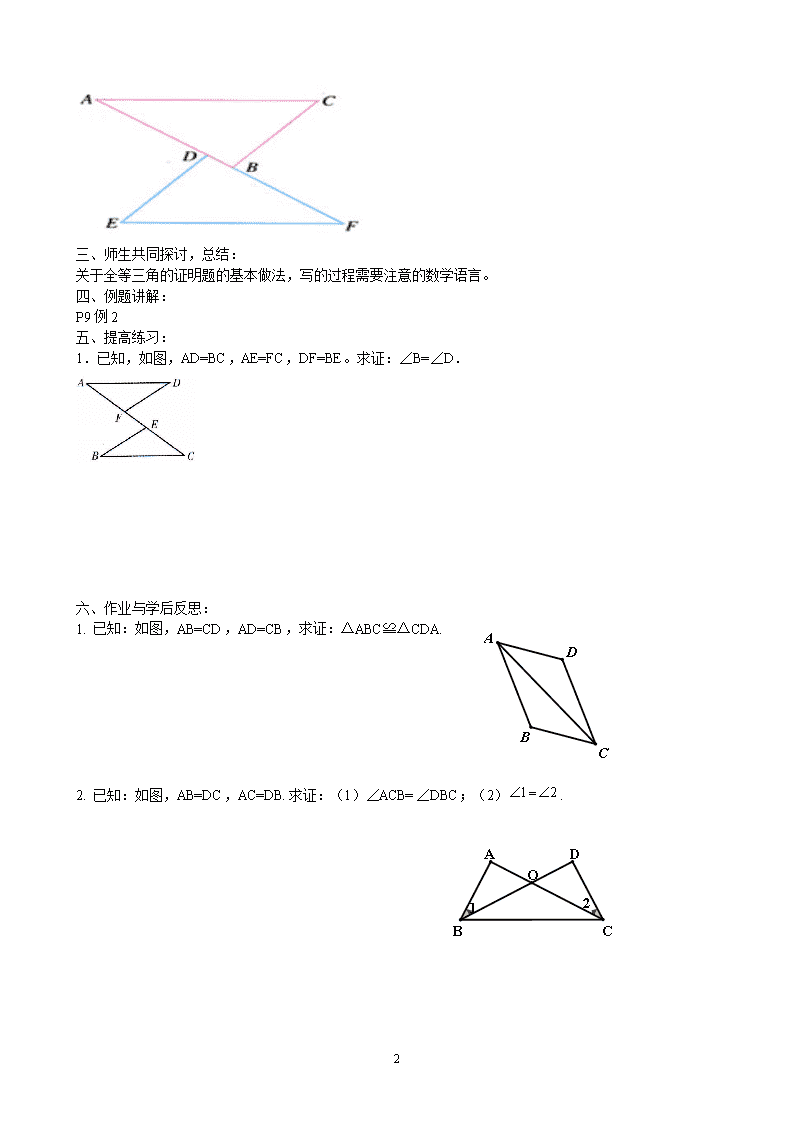
全等三角形导学案

‎12.2全等三角形的判定一（SSS）‎ ‎【学习目标】：‎ ‎1. 经历探索三角形全等条件的过程（即如何用尺规作图：已知三边作三角形），体会利用操作、归纳获得数学结论的过程；‎ ‎2. 记住全等三角形的识别方法（S.S.S），并会运用该方法判断三角形是否全等.‎ ‎【学习重难点】：‎ 理解三边对应相等的两个三角形全等.‎ ‎【自学指导】：‎ 一 、学生看书并理解：‎ 思考:要使两个三角形全等, 是否一定要六个条件呢? 满足下列条件的两个三角形是否一定全等: 一个条件：一边相等的两个三角形或一角相等的两个三角形；两个条件：两个边分别相等的两个三角形，两个角分别相等的两个三角形或一个角和一条边分别相等的三角形；三个条件：三条边分别都相等的两个三角形全等吗？‎ 思考：将三根木条钉成一个三角形木架,这个三角形木架的形状,大小就不变了.你能用“边边边”解释这个事例吗？（三角形的三边长度固定，这个三角形的形状大小就完全确定，这个性质叫三角形的稳定性。）‎ 证明题的普遍出现！理解证明题中证明两个三角形的基本步骤，书写方式要注意那些？‎ 二、自学检测：‎ ‎1.如图，已知AB=DE BC=EF CA=FD 证明△ABC ≌△DEF ‎(对应顶点写在对应的位置)‎ ‎2.如图, △ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证: △ABD≌ △ACD A B C D ‎3.如图，已知AC=FE，BC=DE，点A，D，B，F在一条直线上，AD=FB，证明△ABC ≌△ FDE 3‎ 三、师生共同探讨，总结：‎ 关于全等三角的证明题的基本做法，写的过程需要注意的数学语言。‎ 四、例题讲解：‎ P9例2‎ 五、提高练习：‎ ‎1．已知，如图，AD=BC，AE=FC，DF=BE。求证：∠B=∠D．‎ 六、作业与学后反思：‎ ‎1. 已知：如图，AB=CD，AD=CB，求证：△ABC≌△CDA.‎ ‎ ‎ ‎ ‎ ‎2. 已知：如图，AB=DC，AC=DB.求证：（1）∠ACB=∠DBC；（2）.‎ ‎ ‎ ‎ ‎ 3‎ ‎3. 已知：如图，AB=AC，D是BC中点，‎ ‎（1） 求证：△ABD≌△ACD；（2） 求证：AD⊥BC；‎ ‎（3） 若∠BAD=25°，则∠BAC是多少度？ ‎ ‎4. 已知：如图，四边形ABCD中，AB=AD，BC=DC.求证：∠B=∠D.‎ 3‎