- 2021-04-13 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
两条直线的位置关系 教案(1)
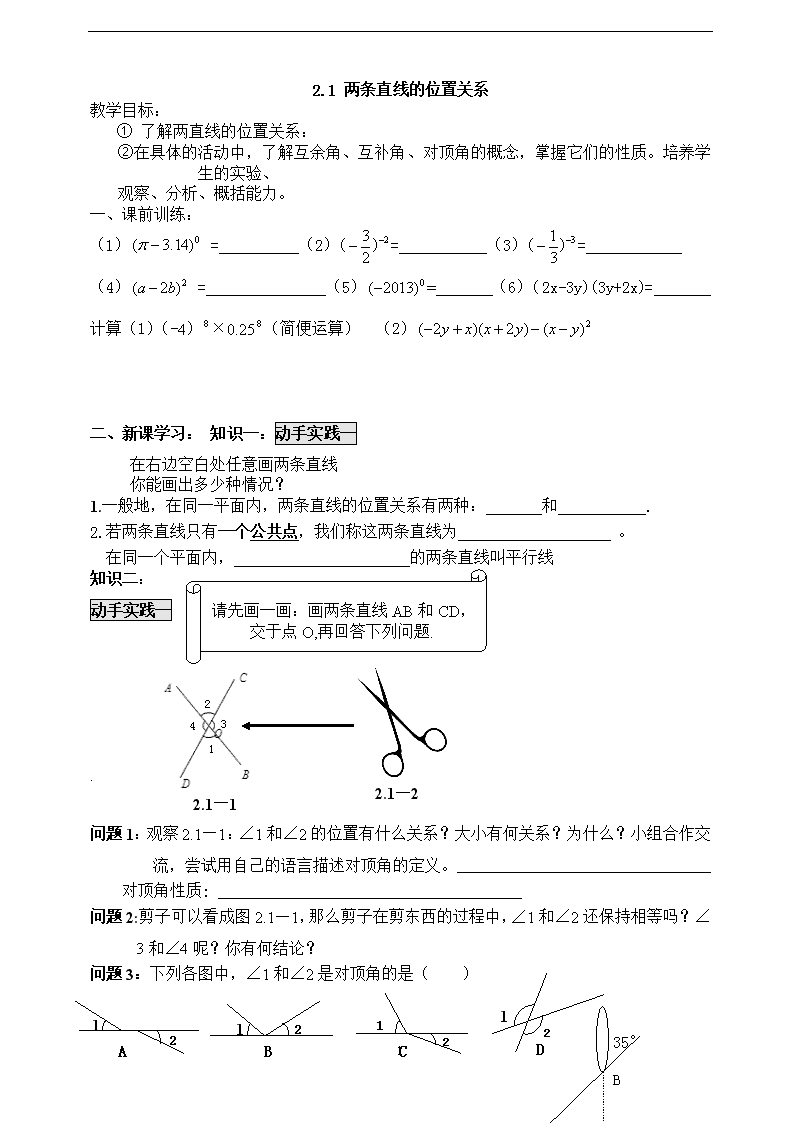
2.1 两条直线的位置关系 教学目标: ① 了解两直线的位置关系: ②在具体的活动中,了解互余角、互补角、对顶角的概念,掌握它们的性质。培养学生的实验、 观察、分析、概括能力。 一、课前训练: (1) = (2)= (3)= (4) = (5)= (6)= 计算(1)(-4)×0.25(简便运算) (2) 二、新课学习: 知识一:动手实践一 在右边空白处任意画两条直线 你能画出多少种情况? 1.一般地,在同一平面内,两条直线的位置关系有两种: 和 . 2.若两条直线只有一个公共点,我们称这两条直线为 。 在同一个平面内, 的两条直线叫平行线 请先画一画:画两条直线AB和CD,交于点O,再回答下列问题. 知识二: 动手实践一 2.1—2 1 2 3 4 2.1—1 . 问题1:观察2.1—1:∠1和∠2的位置有什么关系?大小有何关系?为什么?小组合作交流,尝试用自己的语言描述对顶角的定义。 对顶角性质: 问题2:剪子可以看成图2.1—1,那么剪子在剪东西的过程中,∠1和∠2还保持相等吗?∠3和∠4呢?你有何结论? 1 2 1 2 1 2 1 2 A B C D 问题3:下列各图中,∠1和∠2是对顶角的是( ) A B C 35° 5 问题4:如2.1—3,斜坡上一棵树与山坡所成的角是35°, 则树干与山坡所成的令一个角为( ) A、55° B、45° C、35° D、145° 2.1—3 1.请画出两个角,使他们的和为直角。 2.请画出两个角,使它们的和为平角。 3.小组交流画法,相互点评。 4.用自己的语言描述补角余角的定义。 知识三:动手实践二 在右边空白处作图 补角定义:一般地,如果两个角的和是 ,那么称这两个角互为补角.( 互补) 余角定义:如果两个角的和是 ,那么称这两个角互为余角(互余) 注意:互余与互补是指两个角之间的数量关系,与它们的位置无关。 练习:(1)若∠1=,那么它的余角等于 ,补角等于 。 (2)若∠1=,那么它余角的等于 ,补角等于 。 (3)若一个角的余角为,那么它的补角是 知识四:动手实践三 小组合作交流,解决下列问题: 2 D C O 1 3 4 A N B 2.1—5 1、打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图2.1—4抽象成图2.1—5,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2 则: 2.1—4 (1)如图2.1-5,∠1的余角是 ,∠2的余角是 , (2)若∠1=∠2=300 ,则∠3= 度,∠4= 度。 结论:等角的余角 2、如右图1:已知:∠AOD=∠BOC=900,则 (1)∠COD的余角是∠ 和∠ (2)若∠COD =600 ,则∠AOC= 度,∠BOD= 度 图1 结论:同角的余角 5 3、如右图2,∠1的补角是 ,∠2的补角是 , (2)若∠1=∠2=300 ,则∠AOC= 度,则∠DOB= 度。 图2 结论:等角的补角 4、如右图3,∠AOD的补角是∠ 和∠ , (2)若∠AOD =500 ,则∠1= 度,则∠2= 度。 结论:同角的补角 图3 对应练习:1、如右图4, ∠AOB=∠COD=90° C O A B D 2 1 3 E F 图4 ①. 因为∠1+∠2=90º,∠2+∠3=90º,所以∠1= , 理由是 . ② 因为∠AOC+∠COE=180º,∠EOF+∠COE =180º, 所以∠AOC= ,理由是 . ③若∠3=50º,则∠1= 度。∠2= 度 ∠EOF= 度。∠DOE= 度 2、完成课本P40问题解决与联系拓广 巩固练习: D C O B A 一、填空: 1、如图,O是直线AB上一点,OC是∠AOB的平分线。 ∠AOD=1250,∠AOD的余角是______, ∠BOD=350,∠BOD的余角是______,∠BOC的补角是______ 从右表中,你发现了什么规律? 同一个角的补角比余角大 2、 ∠α α 的余角 α 的补角 5 5° 30° 42° 54° 3、判断: (1)∠1+∠2=90°则∠1是余角. ( ) (2) ∠1 +∠2+ ∠3=90°,则∠1 、∠2、 ∠3、互为余角.( ) (3)如果一个角有补角,那么这个角一定是钝角( ) (4)互补的两个角不可能相等。 ( ) (5) 钝角没有余角,但一定有补角 ( ) 4、如图一所示,若∠AOC=55°,求∠AOD、∠BOC、∠BOD的大小 O A B D C 图5 2.1 两条直线的位置关系预习 1、预习书38、39页 2、回顾:①什么是直角? ②什么是平角? 3、填空:①在一副三角板中,每块都有一个角是90°,那么其余两个角的和是 ②已知∠1=36°,∠2=54°,那么∠1+∠2=_________它们是 关系 ③已知∠1=144°,∠2=36°,那么∠1+∠2=_________它们是 关系 4、判断:(1)如果一个角有补角,那么这个角一定是钝角( ) 5 2.1—13 (2)互补的两个角不可能相等。( ) (3) 钝角没有余角,但一定有补角( ) 5、如图,直线AB与CD交于点O,∠BOC=900,EF经过点O. (1)指出图中所有的对顶角; (2)图中那些角与∠AOE互余?互补? (3)若∠BOF=34°,试求出∠AOF,∠BOE,∠DOE的度数. 提出你的问题 2.1 两条直线的位置关系预习 1、预习书38、39页 2、回顾:①什么是直角? ②什么是平角? 3、填空:①在一副三角板中,每块都有一个角是90°,那么其余两个角的和是 ②已知∠1=36°,∠2=54°,那么∠1+∠2=_________它们是 关系 ③已知∠1=144°,∠2=36°,那么∠1+∠2=_________它们是 关系 4、判断:(1)如果一个角有补角,那么这个角一定是钝角( ) 2.1—13 (2)互补的两个角不可能相等。( ) (3) 钝角没有余角,但一定有补角( ) 5、如图,直线AB与CD交于点O,∠BOC=900,EF经过点O. (1)指出图中所有的对顶角; (2)图中那些角与∠AOE互余?互补? (3)若∠BOF=34°,试求出∠AOF,∠BOE,∠DOE的度数. 提出你的问题 5查看更多