- 2021-04-13 发布 |
- 37.5 KB |
- 7页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学下册 第2章 直线与圆的位置关系 专题分类突破六 切线的判定与性质应用的基本图形练习 (新版)浙教版
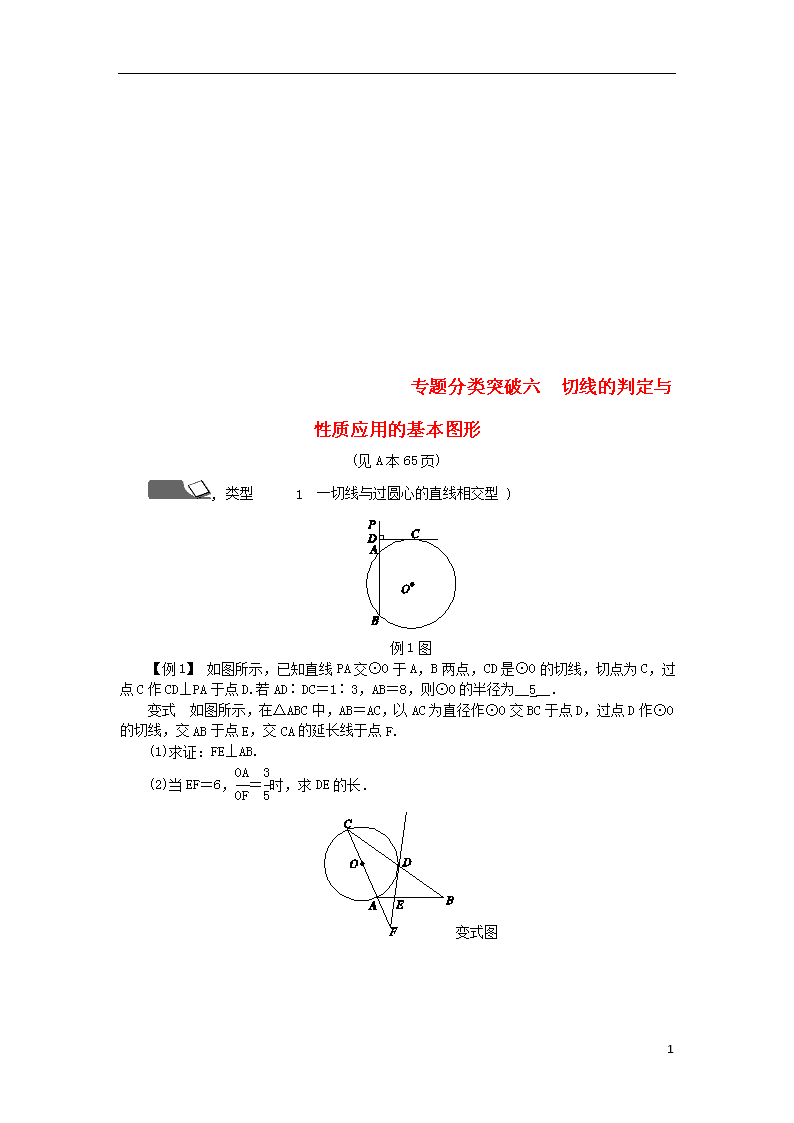
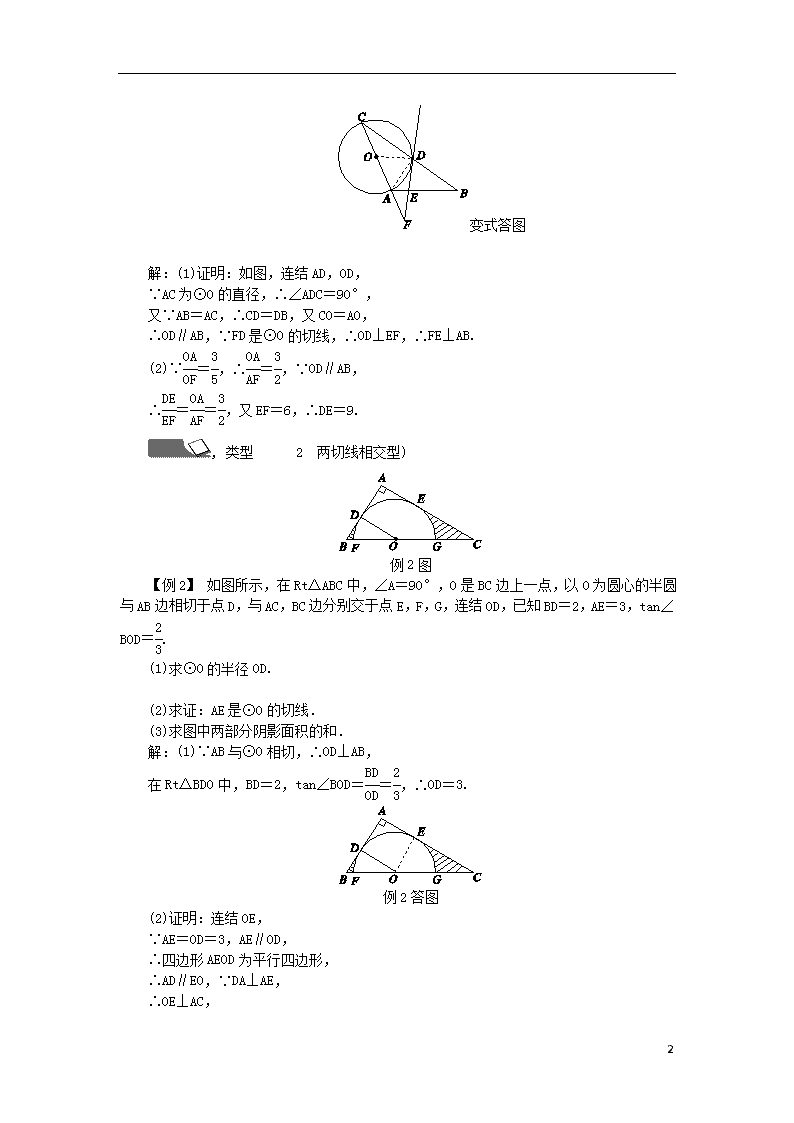
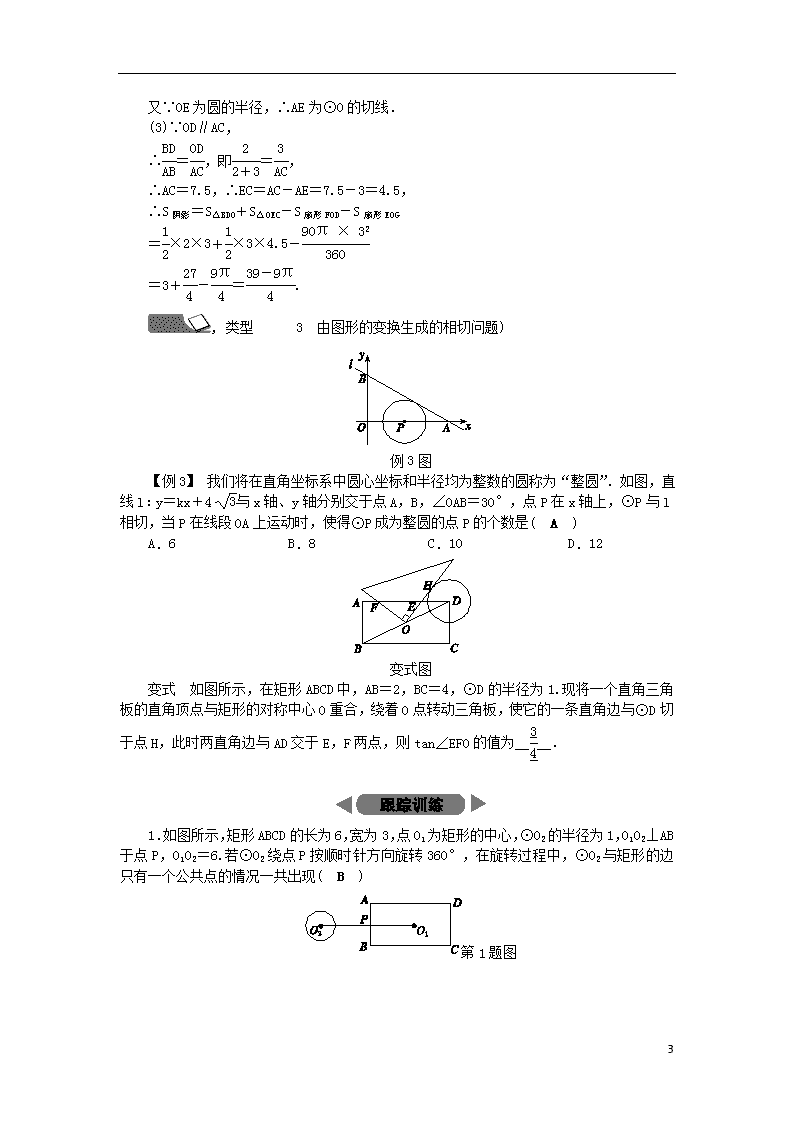
专题分类突破六 切线的判定与性质应用的基本图形 (见A本65页) , 类型 1 一切线与过圆心的直线相交型 ) 例1图 【例1】 如图所示,已知直线PA交⊙O于A,B两点,CD是⊙O的切线,切点为C,过点C作CD⊥PA于点D.若AD∶DC=1∶3,AB=8,则⊙O的半径为__5__. 变式 如图所示,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. (1)求证:FE⊥AB. (2)当EF=6,=时,求DE的长. 变式图 7 变式答图 解:(1)证明:如图,连结AD,OD, ∵AC为⊙O的直径,∴∠ADC=90°, 又∵AB=AC,∴CD=DB,又CO=AO, ∴OD∥AB,∵FD是⊙O的切线,∴OD⊥EF,∴FE⊥AB. (2)∵=,∴=,∵OD∥AB, ∴==,又EF=6,∴DE=9. , 类型 2 两切线相交型) 例2图 【例2】 如图所示,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC,BC边分别交于点E,F,G,连结OD,已知BD=2,AE=3,tan∠BOD=. (1)求⊙O的半径OD. (2)求证:AE是⊙O的切线. (3)求图中两部分阴影面积的和. 解:(1)∵AB与⊙O相切,∴OD⊥AB, 在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3. 例2答图 (2)证明:连结OE, ∵AE=OD=3,AE∥OD, ∴四边形AEOD为平行四边形, ∴AD∥EO,∵DA⊥AE, ∴OE⊥AC, 7 又∵OE为圆的半径,∴AE为⊙O的切线. (3)∵OD∥AC, ∴=,即=, ∴AC=7.5,∴EC=AC-AE=7.5-3=4.5, ∴S阴影=S△BDO+S△OEC-S扇形FOD-S扇形EOG =×2×3+×3×4.5- =3+-=. , 类型 3 由图形的变换生成的相切问题) 例3图 【例3】 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于点A,B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P的个数是( A ) A.6 B.8 C.10 D.12 变式图 变式 如图所示,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为____. 1.如图所示,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( B ) 第1题图 7 A.3次 B.4次 C.5次 D.6次 2.如图所示,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( D ) A.6 B.6 C.9 D.3 第2题图 第3题图 3.如图所示,在△ABC中,BC=8 cm,以A为圆心、2 cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为__8-π__cm2. 第4题图 4.如图所示,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于点E,F. (1)求证:AF⊥EF. (2)小强同学通过探究发现:AF+CF=AB.请你帮助小强同学证明这一结论. 证明:(1)如图所示,连结OD,交BC于点M,则OD⊥EF. ∵OA=OD,∴∠OAD=∠ODA. ∵∠OAD=∠DAC, ∴∠DAC=∠ODA, ∴OD∥AF,∴AF⊥EF. 7 第4题答图 (2)如图所示,连结BD,CD,延长BD,CF交于点G, ∵AB为直径,∴∠ADB=90°. 又∵AD平分∠BAC, ∴AB=AG,GD=DB,CD=DB. ∴CD=GD. ∵AF⊥EF,∴CF=GF, ∴AF+CF=AF+FG=AG,∴AF+CF=AB. 第5题图 5.如图所示,已知直线y=-x+3分别与x轴、y轴交于A,B两点,点P是反比例函数y=-(x<0)图象上的一动点,PH⊥x轴于点H,若以点P为圆心,PH为半径作⊙O,当⊙O与直线AB恰好相切时,求此时OH的长. 解:作PC⊥AB于点C,连结AP, ∵直线y=-x+3分别与x轴、y轴交于A,B, 第5题答图 当y=0时,x=,当x=0时,y=3, ∴A(,0),B(0,3), ∵∠AOB=90°,tan∠OAB==, ∴∠OAB=60°, ∵以P为圆心,PH为半径的圆与直线AB相切, ∴PH=PC,∴AP平分∠OAB, ∴∠PAH=∠OAB=30°, 设OH=x,则AH=x+, ∵PH⊥x轴,∴∠PHA=90°, ∴tan∠PAH=,∴PH=AH·tan 30°=(x+), ∵点P是y=-(x<0)的图象上一点, ∴PH·OH=,即(x+)x=, 7 解得x=(负值舍去), ∴OH=. 6.已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连结BD. (1)在图1中,求证:DB=DI. (2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值. 第6题图 解:(1)证明:如图1,连结BI, ∵I是△ABC的内心, ∴AD平分∠CAB,BI平分∠ABC, ∴∠CAD=∠BAD,∠ABI=∠CBI, ∵∠CAD=∠DBC,∴∠DAB=∠CBD, ∵∠DBI=∠DBC+∠CBI, ∠DIB=∠DAB+∠IBA, ∴∠DIB=∠DBI,∴BD=DI; (2)如图2,连结BD, ∵AB为直径,∴∠ADB=90°, ∵OI⊥AD,∴AD=2DI, ∵BD=DI,∴AD=2BD, ∴AB==BD, ∵DE切圆于D点,∴∠ABD=∠ADE, ∴sin∠ADE=sin∠ABD==. 第6题答图 7 7查看更多