2017中考数学模拟试题含答案(精选5套)

2017中考数学模拟试题含答案(精选5套)

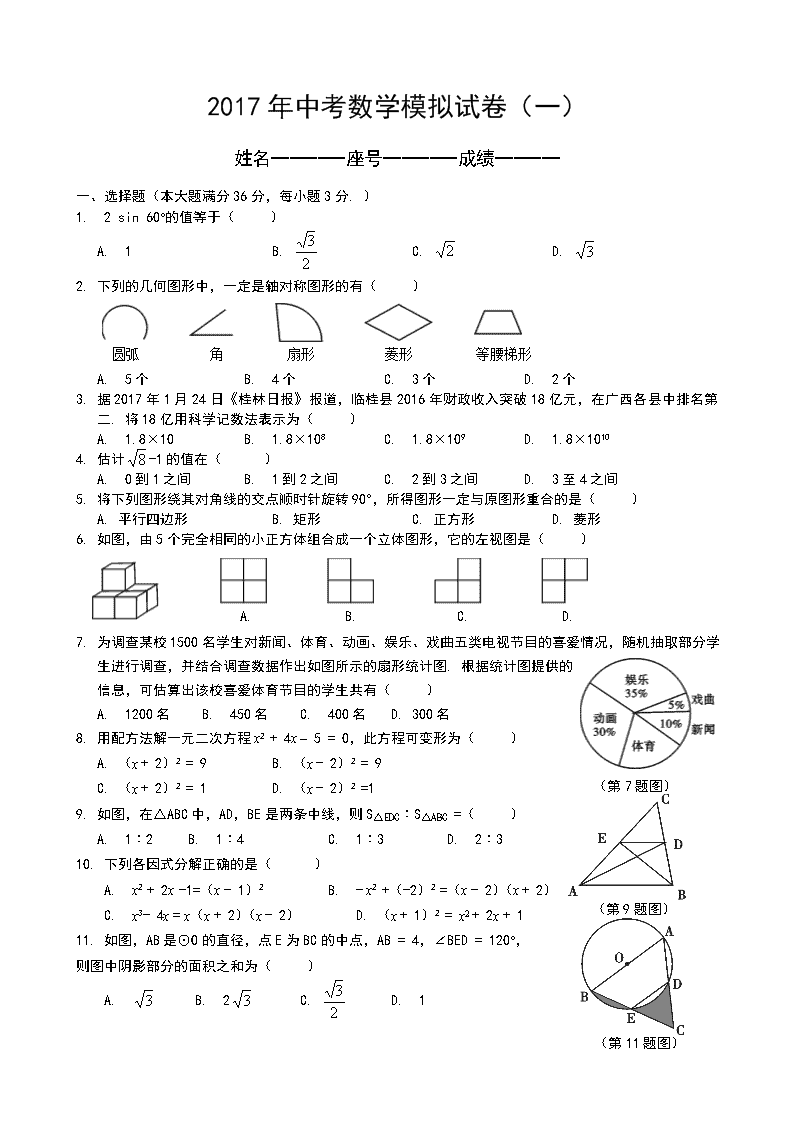
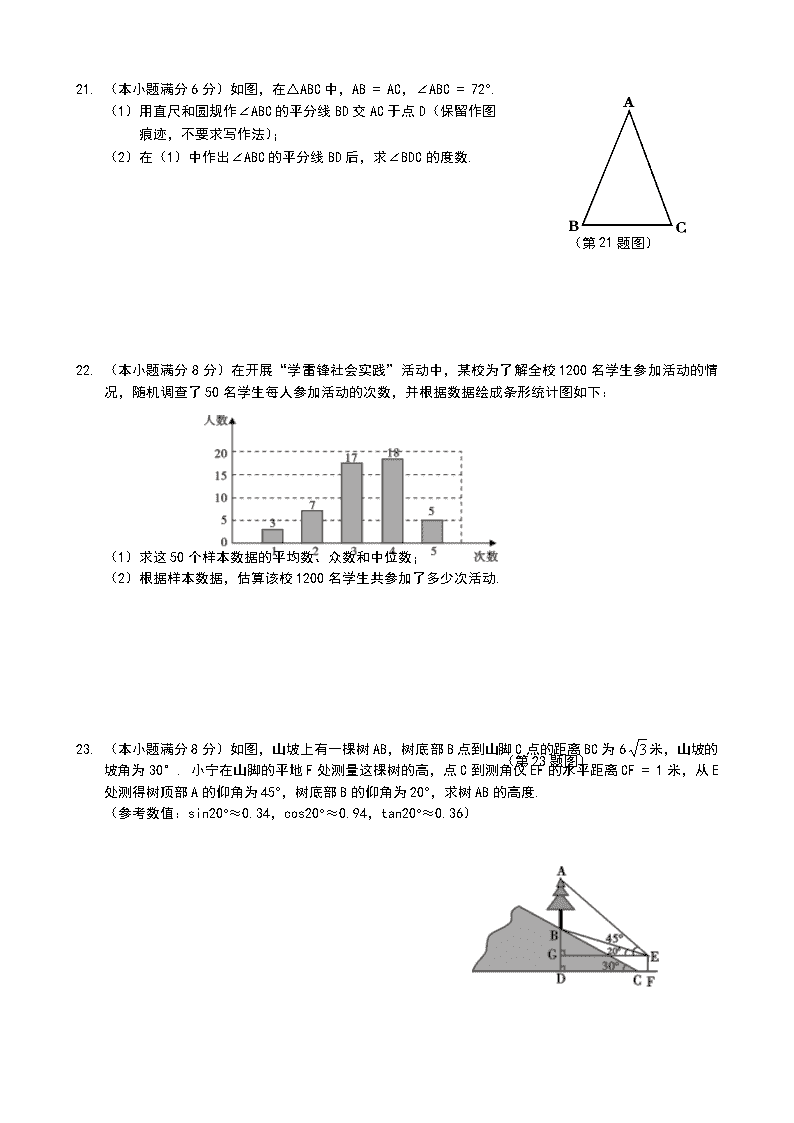
2017 年中考数学模拟试卷（一） 姓名--------座号--------成绩------- 一、选择题（本大题满分 36 分，每小题 3 分. ） 1. 2 sin 60°的值等于（ ） A. 1 B. C. D. 2. 下列的几何图形中，一定是轴对称图形的有（ ） A. 5 个 B. 4 个 C. 3 个 D. 2 个 3. 据 2017 年 1 月 24 日《桂林日报》报道，临桂县 2016 年财政收入突破 18 亿元，在广西各县中排名第 二. 将 18 亿用科学记数法表示为（ ） A. 1.8×10 B. 1.8×108 C. 1.8×109 D. 1.8×1010 4. 估计 -1 的值在（ ） A. 0 到 1 之间 B. 1 到 2 之间 C. 2 到 3 之间 D. 3 至 4 之间 5. 将下列图形绕其对角线的交点顺时针旋转 90°，所得图形一定与原图形重合的是（ ） A. 平行四边形 B. 矩形 C. 正方形 D. 菱形 6. 如图，由 5 个完全相同的小正方体组合成一个立体图形，它的左视图是（ ） 7. 为调查某校 1500 名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学 生进行调查，并结合调查数据作出如图所示的扇形统计图. 根据统计图提供的 信息，可估算出该校喜爱体育节目的学生共有（ ） A. 1200 名 B. 450 名 C. 400 名 D. 300 名 8. 用配方法解一元二次方程 x2 + 4x – 5 = 0，此方程可变形为（ ） A. （x + 2）2 = 9 B. （x - 2）2 = 9 C. （x + 2）2 = 1 D. （x - 2）2 =1 9. 如图，在△ABC 中，AD，BE 是两条中线，则 S△EDC∶S△ABC =（ ） A. 1∶2 B. 1∶4 C. 1∶3 D. 2∶3 10. 下列各因式分解正确的是（ ） A. x2 + 2x -1=（x - 1）2 B. - x2 +（-2）2 =（x - 2）（x + 2） C. x3- 4x = x（x + 2）（x - 2） D. （x + 1）2 = x2 + 2x + 1 11. 如图，AB 是⊙O 的直径，点 E 为 BC 的中点，AB = 4，∠BED = 120°， 则图中阴影部分的面积之和为（ ） A. B. 2 C. D. 1 2 3 2 3 8 3 3 2 3 圆弧 角 扇形 菱形 等腰梯形 A. B. C. D. （第 9 题图） （第 11 题图） （第 7 题图） 12. 如图，△ABC 中，∠C = 90°，M 是 AB 的中点，动点 P 从点 A 出发，沿 AC 方向匀速运动到终点 C，动 点 Q 从点 C 出发，沿 CB 方向匀速运动到终点 B. 已知 P，Q 两点同时出发，并同时到达终点，连接 MP，MQ，PQ . 在整个运动过程中，△MPQ 的面积大小变化情况是 A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小 二、填空题（本大题满分 18 分，每小题 3 分，） 13. 计算：│- │= . 14. 已知一次函数 y = kx + 3 的图象经过第一、二、四象限，则 k 的取值范围是 . 15. 在 10 个外观相同的产品中，有 2 个不合格产品，现从中任意抽取 1 个进行检测，抽到合格产品的概 率是 . 16. 在临桂新区建设中，需要修一段全长 2400m 的道路，为了尽量减少施工对县城交通所造成的影响，实 际工作效率比原计划提高了 20%，结果提前 8 天完成任务，求原计划每天修路的长度. 若设原计划每 天修路 x m，则根据题意可得方程 . 17. 在平面直角坐标系中，规定把一个三角形先沿着 x 轴翻折，再向右平移 2 个单 位称为 1 次变换. 如图，已知等边三角形 ABC 的顶点 B，C 的坐标分别是 （-1，-1），（-3，-1），把△ABC 经过连续 9 次这样的变换得到△A′B′C′， 则点 A 的对应点 A′ 的坐标是 . 18. 如图，已知等腰 Rt△ABC 的直角边长为 1，以 Rt△ABC 的斜边 AC 为直角 边，画第二个等腰 Rt△ACD，再以 Rt△ACD 的斜边 AD 为直角边，画第三 个等腰 Rt△ADE ……依此类推直到第五个等腰 Rt△AFG，则由这五个等 腰直角三角形所构成的图形的面积为 . 三、解答题（本大题 8 题，共 66 分，） 19. （本小题满分 8 分，每题 4 分） （1）计算：4 cos45°- +(π- ) +(-1)3； （2）化简：（1 - ）÷ . 20. （本小题满分 6 分） 3 1 8 3 nm n + 22 nm m − 3 1 2 1 −−+ xx ≤1， ……① 解不等式组： 3（x - 1）＜2 x + 1. ……② （第 12 题图） （第 17 题图） （第 18 题图） ° 21. （本小题满分 6 分）如图，在△ABC 中，AB = AC，∠ABC = 72°. （1）用直尺和圆规作∠ABC 的平分线 BD 交 AC 于点 D（保留作图 痕迹，不要求写作法）； （2）在（1）中作出∠ABC 的平分线 BD 后，求∠BDC 的度数. 22. （本小题满分 8 分）在开展“学雷锋社会实践”活动中，某校为了解全校 1200 名学生参加活动的情 况，随机调查了 50 名学生每人参加活动的次数，并根据数据绘成条形统计图如下： （1）求这 50 个样本数据的平均数、众数和中位数； （2）根据样本数据，估算该校 1200 名学生共参加了多少次活动. 23. （本小题满分 8 分）如图，山坡上有一棵树 AB，树底部 B 点到山脚 C 点的距离 BC 为 6 米，山坡的 坡角为 30°. 小宁在山脚的平地 F 处测量这棵树的高，点 C 到测角仪 EF 的水平距离 CF = 1 米，从 E 处测得树顶部 A 的仰角为 45°，树底部 B 的仰角为 20°，求树 AB 的高度. （参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36） 3 （第 21 题图） （第 23 题图） 24. （本小题满分 8 分）如图，PA，PB 分别与⊙O 相切于点 A，B，点 M 在 PB 上，且 OM∥AP， MN⊥AP，垂足为 N. （1）求证：OM = AN； （2）若⊙O 的半径 R = 3，PA = 9，求 OM 的长. 25. （本小题满分 10 分）某中学计划购买 A 型和 B 型课桌凳共 200 套. 经招标，购买一套 A 型课桌凳比 购买一套 B 型课桌凳少用 40 元，且购买 4 套 A 型和 5 套 B 型课桌凳共需 1820 元. （1）求购买一套 A 型课桌凳和一套 B 型课桌凳各需多少元？ （2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过 40880 元，并且购买 A 型课桌凳的 数量不能超过 B 型课桌凳数量的 ，求该校本次购买 A 型和 B 型课桌凳共有几种方案？哪种方 案的总费用最低？ 26. （本小题满分 12 分）在平面直角坐标系中，现将一块等腰直角三角板 ABC 放在第二象限，斜靠在两 坐标轴上，点 C 为（-1，0）. 如图所示，B 点在抛物线 y = x2 - x – 2 图象上，过点 B 作 BD⊥x 轴， 垂足为 D，且 B 点横坐标为-3. （1）求证：△BDC ≌ △COA； （2）求 BC 所在直线的函数关系式； （3）抛物线的对称轴上是否存在点 P，使△ACP 是以 AC 为直角边的 直角三角形？若存在，求出所有点 P 的坐标；若不存在，请说明理由. 3 2 2 1 2 1 （第 24 题图） （第 26 题图） 2017 年初三适应性检测参考答案与评分意见 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A C B C B D A B C A C 说明：第 12 题是一道几何开放题，学生可从几个特殊的点着手，计算几个特殊三角形面积从而降低 难度，得出答案. 当点 P，Q 分别位于 A、C 两点时，S△MPQ = S△ABC；当点 P、Q 分别运动到 AC，BC 的中点 时，此时，S△MPQ = × AC. BC = S△ABC；当点 P、Q 继续运动到点 C，B 时，S△MPQ = S△ABC，故在整 个运动变化中，△MPQ 的面积是先减小后增大，应选 C. 二、填空题 13. ； 14. k＜0； 15. （若为 扣 1 分）； 16. - = 8； 17. （16，1+ ）； 18. 15.5（或 ）. 三、解答题 19. （1）解：原式 = 4× -2 +1-1……2 分（每错 1 个扣 1 分，错 2 个以上不给分） = 0 …………………………………4 分 （2）解：原式 =（ - ）· …………2 分 = · …………3 分 = m – n …………4 分 20. 解：由①得 3（1 + x）- 2（x-1）≤6， …………1 分 化简得 x≤1. …………3 分 由②得 3x – 3 ＜ 2x + 1， …………4 分 化简得 x＜4. …………5 分 ∴原不等式组的解是 x≤1. …………6 分 21. 解（1）如图所示（作图正确得 3 分） （2）∵BD 平分∠ABC，∠ABC = 72°， 2 1 2 1 2 1 2 1 4 1 2 1 3 1 5 4 10 8 x 2400 x%)201( 2400 + 3 2 31 2 2 2 nm nm + + nm n + m nm 22 − nm m + m nmnm ))(( −+ ∴∠ABD = ∠ABC = 36°， …………4 分 ∵AB = AC，∴∠C =∠ABC = 72°， …………5 分 ∴∠A= 36°， ∴∠BDC =∠A+∠ABD = 36° + 36° = 72°. …………6 分 22. 解：（1）观察条形统计图，可知这组样本数据的平均数是 = =3.3， …………1 分 ∴这组样本数据的平均数是 3.3. …………2 分 ∵在这组样本数据中，4 出现了 18 次，出现的次数最多， ∴这组数据的众数是 4. …………4 分 ∵将这组样本数据按从小到大的顺序排列，其中处在中间的两个数都是 3，有 = 3. ∴这组数据的中位数是 3. ………………6 分 （2）∵这组数据的平均数是 3.3， ∴估计全校 1200 人参加活动次数的总体平均数是 3.3，有 3.3×1200 = 3900. ∴该校学生共参加活动约 3960 次. ………………8 分 23. 解：在 Rt△BDC 中，∠BDC = 90°，BC = 6 米， ∠BCD = 30°， ∴DC = BC·cos30° ……………………1 分 = 6 × = 9， ……………………2 分 ∴DF = DC + CF = 9 + 1 = 10，…………………3 分 ∴GE = DF = 10. …………………4 分 在 Rt△BGE 中，∠BEG = 20°， ∴BG = CG·tan20° …………………5 分 =10×0.36=3.6， …………………6 分 在 Rt△AGE 中，∠AEG = 45°， ∴AG = GE = 10， ……………………7 分 ∴AB = AG – BG = 10 - 3.6 = 6.4. 答：树 AB 的高度约为 6.4 米. ……………8 分 24. 解（1）如图，连接 OA，则 OA⊥AP. ………………1 分 ∵MN⊥AP，∴MN∥OA. ………………2 分 ∵OM∥AP，∴四边形 ANMO 是矩形. ∴OM = AN. ………………3 分 （2）连接 OB，则 OB⊥AP， ∵OA = MN，OA = OB，OM∥BP， ∴OB = MN，∠OMB =∠NPM. 2 1 _ x 50 551841737231 ×+×+×+×+× 2 33+ 3 3 2 3 ∴Rt△OBM≌Rt△MNP. ………………5 分 ∴OM = MP. 设 OM = x，则 NP = 9- x. ………………6 分 在 Rt△MNP 中，有 x2 = 32+（9- x）2. ∴x = 5. 即 OM = 5 …………… 8 分 25. 解：（1）设 A 型每套 x 元，则 B 型每套（x + 40）元. …………… 1 分 ∴4x + 5（x + 40）=1820. ……………………………………… 2 分 ∴x = 180，x + 40 = 220. 即购买一套 A 型课桌凳和一套 B 型课桌凳各需 180 元、220 元. ……………3 分 （2）设购买 A 型课桌凳 a 套，则购买 B 型课桌凳（200 - a）套. a≤ （200 - a）， ∴ …………… 4 分 180 a + 220（200- a）≤40880. 解得 78≤a≤80. …………… 5 分 ∵a 为整数，∴a = 78，79，80 ∴共有 3 种方案. ………………6 分 设购买课桌凳总费用为 y 元，则 y = 180a + 220（200 - a）=-40a + 44000. …………… 7 分 ∵-40＜0，y 随 a 的增大而减小， ∴当 a = 80 时，总费用最低，此时 200- a =120. …………9 分 即总费用最低的方案是： 购买 A 型 80 套，购买 B 型 120 套. ………………10 分 3 2 2017 年中考数学模拟试题（二） 姓名---------座号---------成绩----------- 一、选择题 1、 数 中最大的数是（ ） A、 B、 C、 D、 2、9 的立方根是（ ） A、 B、3 C、 D、 3、已知一元二次方程 的两根 、 ，则 （ ） A、4 B、3 C、-4 D、-3 4、如图是某几何题的三视图，下列判断正确的是（ ） A、几何体是圆柱体，高为 2 B、几何体是圆锥体，高为 2 C、几何体是圆柱体，半径为 2 D、几何体是圆柱体，半径为 2 5、若 ，则下列式子一定成立的是（ ） A、 B、 C、 D、 6、如图 AB∥DE，∠ABC=20°，∠BCD=80°，则∠CDE=（ ） A、20° B、80° C、60° D、100° 7、已知 AB、CD 是⊙O 的直径，则四边形 ACBD 是（ ） A、正方形 B、矩形 C、菱形 D、等腰梯形 8、不等式组 的整数解有（ ） A、0 个 B、5 个 C、6 个 D、无数个 9、已知点 是反比例函数 图像上的点，若 ， 则一定成立的是（ ） A、 B、 C、 D、 10、如图，⊙O 和⊙O′相交于 A、B 两点，且 OO’=5，OA=3， O’B=4，则 AB=( ) A、5 B、2.4 C、2.5 D、4.8 二、填空题 11、正五边形的外角和为 12、计算： 13、分解因式： 14、如图，某飞机于空中 A 处探测到目标 C，此时飞行高度 AC=1200 米，从飞机上看地面控制点 B 的俯 角 ，则飞机 A 到控制点 B 的距离约为 。（结果保留整数） 15、如图，随机闭合开关 A、B、C 中的一个，灯泡发光的概率为 16、已知 ，则 1, 5,0,2− 1− 5 0 2 3± 3 9± 3 9 2 4 3 0x x− + = 1x 2x 1 2x x+ = a b> 0a b+ > 0a b− > 0ab > 0a b > 3 0 2 x x + > − ≥ − 1 1 2 2( , ), ( , )A x y B x y 2y x = 1 20x x> > 1 2 0y y> > 1 20y y> > 1 20 y y> > 2 10y y> > 3m m− ÷ = 2 23 3x y− = 20α = ° 2 2 1 0a a− − = 2 1a a − = A CB B DE C A 2 2 主视图 左视图 俯视图 O B O A ‘ 三、解答题 17、已知点 P（-2,3）在双曲线 上，O 为坐标原点，连接 OP，求 k 的值和线段 OP 的长 18、如图，⊙O 的半径为 2， ，∠C=60°，求 的长 19、观察下列式子 （1）根据上述规律，请猜想，若 n 为正整数，则 n= （2）证明你猜想的结论。 20、某校初三（1）班的同学踊跃为“雅安芦山地震”捐款，根据捐款情况（捐款数为正数）制作以下统 计图表，但生活委员不小心把墨水滴在统计表上，部分数据看不清楚。 （1）全班有多少人捐款？ （2）如果捐款 0~20 元的人数在扇形统计图中所占的圆心角为 72°，那么捐款 21~40 元的有多少人？ ky x =  =AB AC AC 0 1 11 2 1,2 31 2 2 2 1 3 13 4 ,4 53 3 4 4 = × + = × + = × + = × + ⋅⋅⋅ 捐款 人数 0~20 元 21~40 元 41~60 元 61~80 元 6 81 元以上 4 O C B A 81 元 以上 8% 0~20 元 72°61~80 元 41~60 元 32% 21~40 元 21、校运会期间，某班预计用 90 元为班级同学统一购买矿泉水，生活委员发现学校小卖部有优惠活动： 购买瓶装矿泉水打 9 折，经计算按优惠价购买能多买 5 瓶，求每瓶矿泉水的原价和该班实际购买矿泉水的 数量。 22、如图，矩形 OABC 顶点 A(6,0)、C（0,4），直线 分别交 BA、OA 于点 D、E，且 D 为 BA 中 点。 （1）求 k 的值及此时△EAD 的面积； （2）现向矩形内随机投飞镖，求飞镖落在△EAD 内的概率。 （若投在边框上则重投） 23、如图，正方形 ABCD 中，G 是 BC 中点，DE⊥AG 于 E，BF⊥AG 于 F，GN∥DE，M 是 BC 延长线 上一点。 （1）求证：△ABF≌△DAE （2）尺规作图：作∠DCM 的平分线，交 GN 于点 H（保留作图痕迹，不写作法和证明），试证明 GH=AG 1y kx= − B C DA M N G F E C B D A E 24、已知抛物线 （1）若 求该抛物线与 x 轴的交点坐标； （2）若 ，是否存在实数 ,使得相应的 y=1，若有，请指明有几个并证明你的结论，若没有， 阐述理由。 （3）若 且抛物线在 区间上的最小值是-3，求 b 的值。 25.已知等腰 Rt△ABC 和等腰 Rt△AED 中，∠ACB=∠AED=90°，且 AD=AC （1）发现：如图 1，当点 E 在 AB 上且点 C 和点 D 重合时，若点 M、N 分别是 DB、EC 的中点，则 MN 与 EC 的位置关系是　 　，MN 与 EC 的数量关系是　 　 （2）探究：若把（1）小题中的△AED 绕点 A 旋转一定角度，如图 2 所示，连接 BD 和 EC，并连接 DB、 EC 的中点 M、N，则 MN 与 EC 的位置关系和数量关系仍然能成立吗？若成立，请以逆时针旋转 45°得到 的图形（图 3）为例给予证明位置关系成立，以顺时针旋转 45°得到的图形（图 4）为例给予证明数量关系 成立，若不成立，请说明理由． 23 2y ax bx c= + + 1, 1a b c= = = − + + 1a b c = 0x 1 , 23a c b= = + 2 2x− ≤ ≤ 合练习二（数学）参考答案 说明： 1、本解答给出了一种解法供参考，如果考生的解法与本解答不同，各题组可根据试题的主要考查内容比 照评分标准制订相应的评分细则． 2、对于计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可 视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重 的错误，就不再给分． 3、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 一、选择题（本题共 10 小题，每小题 3 分，共 30 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 B D A A B C B B B D 二、填空题（本题共 6 小题，每小题 3 分，共 18 分） 题号 11 12 13 14 15 16 答案 360° -m² 3509 2 三、解答题（本题有 9 个小题, 共 102 分。解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分 9 分） 解：（1）把 代入 ，得 --------4 分 （2）过点 P 作 PE⊥ 轴于点 E，则 OE=2，PE=3 --------6 分 ∴在 △OPE 中， PO= --------9 分 18．（本小题满分 9 分） 解：方法一 连接 OA，OC --------1 分 ∵ ,∠C=60° ∴∠B=60° --------4 分 ∴ ∠AOC=120° --------6 分 ∴ π×2＝ π --------9 分 方法二： ∵ ∴ --------2 分 ∵∠C=60° ∴ --------5 分 ∴ = --------7 分 3( )( )x y x y+ − 1 3 2, 3x y= − = ky x = 6k = − x Rt 2 2 13OE PE+ =  AB AC=  120 180ACl = 4 3  AB AC= AB AC= AB AC BC= =  AB AC= BC ∴ ＝ π --------9 分 19.（本题满分 10 分） （1） ----------3 分 （2）证明：∵ ----------5 分 ----------7 分 ----------8 分 ----------9 分 ∴ ----------10 分 20.（本题满分 10 分） 解：（1） ----------2 分 答：全班有 50 人捐款。 ----------3 分 （2）方法 1：∵捐款 0~20 元的人数在扇形统计图中所占的圆心角为 72° ∴捐款 0~20 元的人数为 ----------6 分 ∴ ----------9 分 答：捐款 21~40 元的有 14 人 ----------10 分 方法 2： ∵捐款 0~20 元的人数在扇形统计图中所占的圆心角为 72° ∴捐款 0~20 元的百分比为 ----------6 分 ∴ ----------9 分 答：捐款 21~40 元的有 14 人 ----------10 分 21.（本题满分 12 分） 方法 1 解：设每瓶矿泉水的原价为 x 元 ----------1 分 ----------5 分 解得： ----------8 分 经检验：x=2 是原方程的解 ----------9 分 ∴ ----------11 分 答：每瓶矿泉水的原价为 2 元，该班实际购买矿泉水 50 瓶。----------12 分 方法 2 解：设每瓶矿泉水的原价为 x 元，该班原计划购买 y 瓶矿泉水 ----------1 分 ----------5 分  1 2 23ACl π= × × 4 3 1 1( 1) nn n n −+ × + 1 1( 1) nn n n −+ × + ( 1)( 1) 1n n n n + −= + 2 1 1n n n −= + 2n n = n= 1 1( 1) nn n n n −= + × − 4 8% 50÷ = 7250 10360 × = 50 10 50 32% 6 4 14− − × − − = 72 1 20%360 5 = = 50 (1 20% 32% 6 50 8%) 14× − − − ÷ − = 90 90 50.9x x − = 2x = 90 2 5 50÷ + = 90 0.9 ( 5) 90 xy x y =  + = 解得： ----------9 分 ∴ ----------11 分 答：每瓶矿泉水的原价为 2 元，该班实际购买矿泉水 50 瓶。----------12 分 22．（本小题满分 12 分） 解：（1）∵矩形 OABC 顶点 A（6，0）、C（0，4） ∴B（6，4） --------1 分 ∵ D 为 BA 中点 ∴ D（6，2），AD=2 --------2 分 把点 D（6，2）代入 得 k= --------4 分 令 得 ∴ E（2，0） --------5 分 ∴ OE=2，AE=4 --------7 分 ∴ = = --------9 分 （2）由（1）得 --------10 分 ∴ --------12 分 23.（本题满分 12 分） 解：∵ 四边形 ABCD 是正方形 ∴ AB=BC=CD=DA ----------1 分 ∠DAB=∠ABC=90° ∴ ∠DAE+∠GAB=90° ∵ DE⊥AG BF⊥AG ∴ ∠AED=∠BFA=90° ∠DAE +∠ADE=90° ∴ ∠GAB =∠ADE ----------3 分 在△ABF 和△DAE 中 ∴ △ABF≌△DAE ----------5 分 （2）作图略 ----------7 分 方法 1：作 HI⊥BM 于点 I ----------8 分 ∵ GN∥DE ∴ ∠AGH=∠AED=90° ∴ ∠AGB+∠HGI=90° ∵ HI⊥BM ∴ ∠GHI+∠HGI=90° ∴ ∠AGB =∠GHI ----------9 分 ∵ G 是 BC 中点 2 45 x y =  = 45 5 50+ = 1y kx= − 1 2 0y = 2x = EADS 1 4 22 × × 4 24OABCS =矩形 6 1 24 6EADP = = ( 飞镖落在 内) ADE BAF BFA AED AB DA ∠ = ∠ ∠ = ∠  = F E GB C A D M N ∴ tan∠AGB= ∴ tan∠GHI= tan∠AGB= ∴ GI=2HI ----------10 分 ∵ CH 平分∠DCM ∴ ∠HCI= ∴ CI=HI ∴ CI=CG=BG=HI ----------11 分 在△ABG 和△GIH 中 ∴ △ABG≌△GIH ∴ AG=GH ----------12 分 方法 2： 作 AB 中点 P，连结 GP ----------8 分 ∵ P、G 分别是 AB、BC 中点 且 AB=BC ∴ AP=BP=BG=CG ----------9 分 ∴ ∠BPG=45° ∵ CH 平分∠DCM ∴ ∠HCM= ∴ ∠APG=∠HCG=135° ----------10 分 ∵ GN∥DE ∴ ∠AGH=∠AED=90° ∴ ∠AGB+∠HGM=90° ∵ ∠BAG+∠AGB=90° ∴ ∠BAG =∠HGM ----------11 分 在△AGP 和△GHC 中 ∴ △AGP≌△GHC ∴ AG=GH ----------12 分 24.（本题满分 14 分） 解（1）当 ， 时，抛物线为 ， ∵方程 的两个根为 ， ． ∴该抛物线与 轴公共点的坐标是 和 ． --------------------------------3 分 （2）由 得 ， 2AB BG = 2GI HI = 1 452 DCM∠ = ° ABG GIH BG IH AGB GHI ∠ = ∠  = ∠ = ∠ 1 452 DCM∠ = ° PAG CGH AP GC AGP GHC ∠ = ∠  = ∠ = ∠ 1== ba 1−=c 123 2 −+= xxy 0123 2 =−+ xx 11 −=x 3 1 2 =x x ( )1 0− ， 1 03     ， 1y = 23 2 1ax bx c+ + = ----------------------5 分 ， --------------------------------7 分 所以方程 有两个不相等实数根， 即存在两个不同实数 ，使得相应 ．-------------------------8 分 （3） ，则抛物线可化为 ，其对称轴为 ， 当 时，即 ，则有抛物线在 时取最小值为-3，此时 - ，解得 ，合题意--------------10 分 当 时，即 ，则有抛物线在 时取最小值为-3，此时- ，解得 ，不合题意，舍去.--------------12 分 当 时 ， 即 ， 则 有 抛 物 线 在 时 取 最 小 值 为 -3 ， 此 时 ，化简得： ，解得： （不合题意，舍去）， . --------------14 分 综上： 或 25.（本题满分 14 分） 解：解：（1） .------------2 分 （2）连接 EM 并延长到 F，使 EM=MF，连接 CM、CF、 BF. ------------3 分 ∵BM=MD,∠EMD=∠BMF， ∴△EDM≌△FBM ∴BF=DE=AE，∠FBM=∠EDM=135° ∴∠FBC=∠EAC=90°---------5 分 ∴△EAC≌△FBC ∴FC=EC, ∠FCB=∠ECA---------6 分 ∴∠ECF=∠FCB+∠BCE =∠ECA+∠BCE=90° 24 12 ( 1)b a c∆ = − − 2 2 2 2 24 12 ( ) 4 12 12 4( 3 3 )b a a b b ab a b ab a= − − − = + + = + + 2 23 34[( ) ]2 4b a a= + + 0, 0a ≠ ∴ >Q V 23 2 1ax bx c+ + = 0x 1y = 1 , 23a c b= − = 2 2 2y x bx b= + + + x b= − 2x b= − −＜ 2b > 2x = − 23 ( 2) 2 ( 2) 2b b= − + × − + + 3b = 2x b= − ＞ 2b < − 2x = 23 2 2 2 2b b= + × + + 9 5b = − 2 b− −≤ ≤2 2 b− ≤ ≤2 x b= − 23 ( ) 2 ( ) 2b b b b− = − + × − + + 2 5 0b b− − = 1 21 2b += 1 21 2b −= 3b = 1 21 2b −= 1, 2MN EC MN EC⊥ = A B C FM N DE 又点 M、N 分别是 EF、EC 的中点 ∴MN∥FC ∴MN⊥FC---------8 分 （可把 Rt△EAC 绕点 C 旋转 90°得到 Rt△CBF,连接 MF,ME,MC,然后证明三点共线） 证法 2：延长 ED 到 F，连接 AF、MF，则 AF 为矩形 ACFE 对角线，所以比经过 EC 的中点 N 且 AN=NF=EN=NC.----------------------------4 分 在 Rt△BDF 中，M 是 BD 的中点，∠B=45° ∴FD=FB ∴FM⊥AB， ∴MN=NA=NF=NC---------------------5 分 ∴点 A、C、F、M 都在以 N 为圆心的圆上 ∴∠MNC=2∠DAC--------------------6 分 由四边形 MACF 中，∠MFC=135° ∠FMA=∠ACB=90° ∴∠DAC=45° ∴∠MNC=90°即 MN⊥FC-------------------8 分 （还有其他证法，相应给分） （3）连接 EF 并延长交 BC 于 F，------------------9 分 ∵∠AED=∠ACB=90° ∴DE∥BC ∴∠DEM=∠AFM，∠EDM=∠MBF 又 BM=MD ∴△EDM≌△FBM-----------------11 分 ∴BF=DE=AE,EM=FM ∴ --------------14 分 （另证：也可连接 DN 并延长交 BC 于 M） 备注：任意旋转都成立，如下图证明两个红色三角形全等。其中∠EAC=∠CBF 的证明， 可延长 ED 交 BC 于 G，通过角的转换得到 1 1 1 1( ) ( )2 2 2 2MN FC BC BF AC AE EC= = − = − = F C B A N M DE A B C F N M D E 2017 年中考数学模拟试卷（三） 　 一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分．请将正确选项的字母代号填涂在答题卡相应位 置上） 1．（3 分）﹣3 相反数是（　　） 　A． B．﹣3 C．﹣ D．3 考点：相反数．3797161 分析：根据只有符号不同的两个数互为相反数解答． 解答：解：﹣3 相反数是 3． 故选 D． 点评：本题主要考查了互为相反数的定义，熟记定义是解题的关键． 　 2．（3 分）下列运算正确的是（　　） 　A． B．（m2）3=m5 C．a2•a3=a5 D．（x+y）2=x2+y2 考点：完全平方公式；算术平方根；同底数幂的乘法；幂的乘方与积的乘方．3797161 专题：计算题． 分析：A、利用平方根定义化简得到结果，即可做出判断； B、利用幂的乘方运算法则计算得到结果，即可做出判断； C、利用同底数幂的乘法法则计算得到结果，即可做出判断； D、利用完全平方公式展开得到结果，即可做出判断． 解答：解：A、 =3，本选项错误； B、（m2）3=m6，本选项错误； C、a2•a3=a5，本选项正确； D、（x+y）2=x2+y2+2xy，本选项错误， 故选 C 点评：此题考查了完全平方公式，合并同类项，同底数幂的乘法，以及平方差公式，熟练掌握公式 及法则是解本题的关键． 　 3．下列图形中，不是中心对称图形是（　　） 　A．矩形 B．菱形 C．正五边形 D．正八边形 考点：中心对称图形．3797161 F C B A M N D E 分析：根据中心对称图形的概念和各图形的特点即可解答． 解答：解：只有正五边形是奇数边形，绕中心旋转 180 度后所得的图形与原图形不会重合． 故选 C． 点评：本题考查中心对称图形的定义：绕对称中心旋转 180 度后所得的图形与原图形完全重合，正 奇边形一定不是中心对称图形． 　 4．（3 分）（2012•宁德）已知正 n 边形的一个内角为 135°，则边数 n 的值是（　　） 　A．6 B．7 C．8 D．10 考点：多边形内角与外角．3797161 分析：根据多边形的相邻的内角与外角互为邻补角求出每一个外角的度数，再根据多边形的边数等 于外角和除以每一个外角的度数进行计算即可得解． 解答：解：∵正 n 边形的一个内角为 135°， ∴正 n 边形的一个外角为 180°﹣135°=45°， n=360°÷45°=8． 故选 C． 点评：本题考查了多边形的外角，利用多边形的边数等于外角和除以每一个外角的度数是常用的方 法，求出多边形的每一个外角的度数是解题的关键． 　 5．（3 分）（2010•眉山）下列说法不正确的是（　　） 　A．某种彩票中奖的概率是 ，买 1000 张该种彩票一定会中奖 　B．了解一批电视机的使用寿命适合用抽样调查 　C．若甲组数据的标准差 S 甲=0.31，乙组数据的标准差 S 乙=0.25，则乙组数据比甲组数据稳定 　D．在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件 考点：概率公式；全面调查与抽样调查；标准差；随机事件；可能性的大小．3797161 专题：压轴题． 分析：根据抽样调查适用的条件、方差的定义及意义和可能性的大小找到正确答案即可． 解答：解：A、某种彩票中奖的概率是 ，只是一种可能性，买 1000 张该种彩票不一定会中奖， 故错误； B、调查电视机的使用寿命要毁坏电视机，有破坏性，适合用抽样调查，故正确； C、标准差反映了一组数据的波动情况，标准差越小，数据越稳定，故正确； D、袋中没有黑球，摸出黑球是不可能事件，故正确． 故选 A． 点评：用到的知识点为：破坏性较强的调查应采用抽样调查的方式；随机事件可能发生，也可能不 发生；标准差越小，数据越稳定；一定不会发生的事件是不可能事件． 　 6．（3 分）（2010•海南）在反比例函数 y= 的图象的每一条曲线上，y 都随 x 的增大而增大，则 k 的 值可以是（　　） 　A．﹣1 B．0 C．1 D．2 考点：反比例函数的性质．3797161 专题：压轴题． 分析：对于函数 来说，当 k＜0 时，每一条曲线上，y 随 x 的增大而增大；当 k＞0 时，每一条 曲线上，y 随 x 的增大而减小． 解答：解：反比例函数 的图象上的每一条曲线上，y 随 x 的增大而增大，所以 1﹣k＜0，解 得 k＞1． 故选 D． 点评：本题考查反比例函数的增减性的判定．在解题时，要注意整体思想的运用．易错易混点：学 生对解析式 中 k 的意义不理解，直接认为 k＜0，错选 A． 　 7．（3 分）（2013•江都市模拟）如图，是某几何体的三视图及相关数据，则该几何体的侧面积是（　　） 　A．10π B．15π C．20π D．30π 考点：圆锥的计算；由三视图判断几何体．3797161 分析：根据三视图可以判定此几何体为圆锥，根据三视图的尺寸可以知圆锥的底面半径为 3，圆锥 的母线长为 5，代入公式求得即可． 解答：解：由三视图可知此几何体为圆锥， ∴圆锥的底面半径为 3，母线长为 5， ∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长， ∴圆锥的底面周长=圆锥的侧面展开扇形的弧长=2πr=2π×3=6π， ∴圆锥的侧面积= = ×6π×5=15π， 故选 B． 点评：本题考查了圆锥的侧面积的计算，解题的关键是正确的理解圆锥的底面周长等于圆锥的侧面 展开扇形的面积． 　 8．（3 分）（2013•惠山区一模）已知点 A，B 分别在反比例函数 y= （x＞0），y= （x＞0）的图象 上且 OA⊥OB，则 tanB 为（　　） 　A． B． C． D． 考点 ： 反比例函数综合题．3797161 专题 ： 压轴题；探究型． 分析 ： 首先设出点 A 和点 B 的坐标分别为：（x1， ）、（x2，﹣ ），设线段 OA 所在的直线的解析式为：y=k1x， 线段 OB 所在的直线的解析式为：y=k2x，然后根据 OA⊥OB，得到 k1k2= •（﹣ ）=﹣1，然后利用正切的定 义进行化简求值即可． 解答 ： 解：设点 A 的坐标为（x1， ），点 B 的坐标为（x2，﹣ ）， 设线段 OA 所在的直线的解析式为：y=k1x，线段 OB 所在的直线的解析式为：y=k2x， 则 k1= ，k2=﹣ ， ∵OA⊥OB， ∴k1k2= •（﹣ ）=﹣1 整理得：（x1x2）2=16， ∴tanB= = = = = = = ． 故选 B． 点评 ： 本题考查的是反比例函数综合题，解题的关键是设出 A、B 两点的坐标，然后利用互相垂直的两条直线的比例系 数互为负倒数求解． 　 二、填空题（本大题共有 10 小题，每小题 3 分，共 30 分.不需写出解答过程，请把答案直接填写在答题 卡相应位置上） 9．（3 分）PM 2.5 是指大气中直径小于或等于 0.0000025m 的颗粒物，将 0.0000025 用科学记数法表示为　 2.5×10﹣6　． 考点：科学记数法—表示较小的数．3797161 分析：绝对值小于 1 的正数也可以利用科学记数法表示，一般形式为 a×10﹣n，与较大数的科学记数 法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的 0 的个数 所决定． 解答：解：0.0000025=2.5×10﹣6， 故答案为：2.5×10﹣6． 点评：本题考查用科学记数法表示较小的数，一般形式为 a×10﹣n，其中 1≤|a|＜10，n 为由原数左边 起第一个不为零的数字前面的 0 的个数所决定． 　 10．（3 分）（2011•邵阳）函数 y= 中，自变量 x 的取值范围是　x≥1　． 考点：函数自变量的取值范围；二次根式有意义的条件．3797161 专题：计算题． 分析：根据二次根式的意义，有 x﹣1≥0，解不等式即可． 解答：解：根据二次根式的意义，有 x﹣1≥0， 解可 x≥1， 故自变量 x 的取值范围是 x≥1． 点评：本题考查了二次根式的意义，只需保证被开方数大于等于 0 即可． 　 11．（3 分）分解因式：m3﹣4m2+4m=　m（m﹣2）2　． 考点：提公因式法与公式法的综合运用．3797161 分析：先提取公因式 m，再对余下的多项式利用完全平方公式继续分解． 解答：解：m3﹣4m2+4m =m（m2﹣4m+4） =m（m﹣2）2． 故答案为：m（m﹣2）2． 点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然 后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止． 　 12．（3 分）（2013•江都市模拟）已知⊙O1 与⊙O2 相交，两圆半径分别为 2 和 m，且圆心距为 7，则 m 的取值范围是　5＜m＜9　． 考点：圆与圆的位置关系．3797161 分析：两圆相交，圆心距是 7，根据两圆位置关系与圆心距 d，两圆半径 R，r 的数量关系间的联系 即可求得另一圆的半径的取值范围，继而求得答案． 解答：解：∵⊙O1 与⊙O2 相交，圆心距是 7， 又∵7﹣2=5，7+2=9， ∴半径 m 的取值范围为：5＜m＜9． 故答案为：5＜m＜9． 点评：此题考查了圆与圆的位置关系．解题的关键是注意掌握两圆位置关系与圆心距 d，两圆半径 R ，r 的数量关系间的联系． 　 13．（3 分）（2013•江都市模拟）若点（a，b）在一次函数 y=2x﹣3 上，则代数式 3b﹣6a+1 的值是　﹣8　 ． 考点：一次函数图象上点的坐标特征．3797161 分析：先把点（a，b）代入一次函数 y=2x﹣3 求出 2a﹣b 的值，再代入代数式进行计算即可． 解答：解：∵点（a，b）在一次函数 y=2x﹣3 上， ∴b=2a﹣3，即 2a﹣b=3， ∴原式=﹣3（2a﹣b）+1=（﹣3）×3+1=﹣8． 故答案为：﹣8． 点评：本题考查的是一次函数图象上点的坐标特点，即一次函数图象上各点的坐标一定适合此函数 的解析式． 　 14．（3 分）（2011•枣阳市模拟）方程 的解为 x=　9　． 考点：解分式方程．3797161 专题：计算题． 分析：本题考查解分式方程的能力，观察可得方程最简公分母为 x（x﹣3），去分母，转化为整式 方程求解．结果要检验． 解答：解：方程两边同乘 x（x﹣3），得 2x=3（x﹣3）， 解得 x=9． 经检验 x=9 是原方程的解． 点评：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解． （2）解分式方程一定注意要验根． 　 15．（3 分）（2013•江都市模拟）如图，⊙O 的直径 CD⊥EF，∠OEG=30°，则∠DCF=　30　°． 考点：圆周角定理；垂径定理．3797161 分析： 由⊙O 的直径 CD⊥EF，由垂径定理可得 = ，又由∠OEG=30°，∠EOG 的度数，又由圆周 角定理，即可求得答案． 解答：解：∵⊙O 的直径 CD⊥EF， ∴ = ， ∵∠OEG=30°， ∴∠EOG=90°﹣∠OEG=60°， ∴∠DCF= ∠EOG=30°． 故答案为：30°． 点评：此题考查了圆周角定理与垂径定理．此题难度不大，注意掌握数形结合思想的应用． 　 16．（3 分）如图是二次函数 和一次函数 y2=kx+t 的图象，当 y1≥y2 时，x 的取值范围是　 ﹣1≤x≤2　． 考点：二次函数与不等式（组）．3797161 分析：根据图象可以直接回答，使得 y1≥y2 的自变量 x 的取值范围就是直线 y1=kx+m 落在二次函数 y2=ax2+bx+c 的图象上方的部分对应的自变量 x 的取值范围． 解答：解：根据图象可得出：当 y1≥y2 时，x 的取值范围是：﹣1≤x≤2． 故答案为：﹣1≤x≤2． 点评：本题考查了二次函数的性质．本题采用了“数形结合”的数学思想，使问题变得更形象、直观， 降低了题的难度． 　 17．（3 分）（2013•江都市模拟）如图，点 E、F 分别是正方形纸片 ABCD 的边 BC、CD 上一点，将正 方形纸片 ABCD 分别沿 AE、AF 折叠，使得点 B、D 恰好都落在点 G 处，且 EG=2，FG=3，则正方形纸 片 ABCD 的边长为　6　． 考点：翻折变换（折叠问题）．3797161 分析：设正方形 ABCD 的边长为 x，根据翻折变换的知识可知 BE=EG=2，DF=GF=3，则 EC=x﹣2， FC=x﹣3，在 Rt△EFC 中，根据勾股定理列出式子即可求得边长 x 的长度． 解答：解：设正方形 ABCD 的边长为 x， 根据折叠的性质可知：BE=EG=2，DF=GF=3， 则 EC=x﹣2，FC=x﹣3， 在 Rt△EFC 中，EC2+FC2=EF2， 即（x﹣2）2+（x﹣3）2=（2+3）2， 解得：x1=6，x2=﹣1（舍去）， 故正方形纸片 ABCD 的边长为 6． 故答案为：6． 点评：本题考查了翻折变换的知识，解答本题的关键是熟练掌握翻折变换的性质：翻折前后对应边 相等，另外要求同学们熟练掌握勾股定理的应用． 　 18．（3 分）（2013•惠山区一模）图 1 是一个八角星形纸板，图中有八个直角，八个相等的钝角，每条边 都相等．如图 2 将纸板沿虚线进行切割，无缝隙无重叠的拼成图 3 所示的大正方形，其面积为 8+4 ，则 图 3 中线段 AB 的长为　 +1　． 考点：剪纸问题；一元二次方程的应用；正方形的性质．3797161 专题：几何图形问题；压轴题． 分析：根据题中信息可得图 2、图 3 面积相等；图 2 可分割为一个正方形和四个小三角形；设原八 角形边长为 a，则图 2 正方形边长为 2a+ a、面积为（2a+ a）2，四个小三角形面积和为 2a2 ，解得 a=1．AB 就知道等于多少了． 解答：解：设原八角形边长为 a，则图 2 正方形边长为 2a+ a、面积为（2a+ a）2，四个小三角 形面积和为 2a2， 列式得（2a+ a）2+2a2=8+4 ，解得 a=1，则 AB=1+ ． 点评：解此题的关键是抓住图 3 中的 AB 在图 2 中是哪两条线段组成的，再列出方程求出即可． 　 三、解答题：（本大题共有 10 小题，共 96 分．请在答题卡指定区域内作答，解答时应写出文字说明、证 明过程或演算步骤） 19．（10 分）（1）计算：2﹣1+ cos30°+|﹣5|﹣（π﹣2013）0． （2）化简：（1+ ）÷ ． 考点：分式的混合运算；实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．3797161 专题：计算题． 分析：（1）根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式= + × +5﹣1，再进 行二次根式的乘法运算，然后进行有理数的加减运算； （2）先把括号内通分和把除法化为乘法，然后把分子分解后约分即可． 解答：（1）解：原式= + × +5﹣1 = + +5﹣1 =6； （2）原式= • =x． 点评：本题考查了分式的混合运算：先把分式的分子或分母因式分解，再进行通分或约分，得到最 简分式或整式．也考查了零指数幂、负整数指数幂和特殊角的三角函数值． 　 20．（6 分）解不等式组 ，并将解集在数轴上表示． 考点：解一元一次不等式组；在数轴上表示不等式的解集．3797161 分析：求出每个不等式的解集，找出不等式组的解集即可． 解答：解： ∵由①得，x＜2， 由②得，x≥﹣1， ∴不等式组的解集是：﹣1≤x＜2， 在数轴上表示不等式组的解集为 ． 点评：本题考查了解一元一次不等式（组），在数轴上表示不等式组的解集的应用，关键是能根据 不等式的解集找出不等式组的解集． 　 21．（8 分）（2011•青岛）图 1 是某城市三月份 1 至 8 日的日最高气温随时间变化的折线统计图，小刚根 据图 1 将数据统计整理后制成了图 2． 根据图中信息，解答下列问题： （1）将图 2 补充完整； （2）这 8 天的日最高气温的中位数是　2.5　℃； （3）计算这 8 天的日最高气温的平均数． 考点：折线统计图；条形统计图；算术平均数；中位数．3797161 分析：（1）从（1）可看出 3℃的有 3 天． （2）中位数是数据从小到大排列在中间位置的数． （3）求加权平均数数，8 天的温度和÷8 就为所求． 解答：解：（1）如图所示． （2）∵这 8 天的气温从高到低排列为：4，3，3，3，2，2，1，1 ∴中位数应该是第 4 个数和第 5 个数的平均数：（2+3）÷2=2.5． （3）（1×2+2×2+3×3+4×1）÷8=2.375℃． 8 天气温的平均数是 2.375． 点评：本题考查了折线统计图，条形统计图的特点，以及中位数的概念和加权平均数的知识点． 　 22．（6 分）（2012•苏州）在 3×3 的方格纸中，点 A、B、C、D、E、F 分别位于如图所示的小正方形的 顶点上． （1）从 A、D、E、F 四个点中任意取一点，以所取的这一点及点 B、C 为顶点画三角形，则所画三角形 是等腰三角形的概率是　 　； （2）从 A、D、E、F 四个点中先后任意取两个不同的点，以所取的这两点及点 B、C 为顶点画四边形， 求所画四边形是平行四边形的概率是　 　（用树状图或列表法求解）． 考点：列表法与树状图法；等腰三角形的判定；平行四边形的判定．3797161 分析：（1）根据从 A、D、E、F 四个点中任意取一点，一共有 4 种可能，只有选取 D 点时，所画 三角形是等腰三角形，即可得出答案； （2）利用树状图得出从 A、D、E、F 四个点中先后任意取两个不同的点，一共有 12 种可能， 进而得出以点 A、E、B、C 为顶点及以 D、F、B、C 为顶点所画的四边形是平行四边形，即 可求出概率． 解答：解：（1）根据从 A、D、E、F 四个点中任意取一点，一共有 4 种可能，只有选取 D 点时， 所画三角形是等腰三角形， 故 P（所画三角形是等腰三角形）= ； （2）用“树状图”或利用表格列出所有可能的结果： ∵以点 A、E、B、C 为顶点及以 D、F、B、C 为顶点所画的四边形是平行四边形， ∴所画的四边形是平行四边形的概率 P= = ． 故答案为：（1） ，（2） ． 点评：此题主要考查了利用树状图求概率，根据已知正确列举出所有结果，进而得出概率是解题关 键． 　 23．（8 分）在一次数学活动课上，数学老师在同一平面内将一副直角三角板如图位置摆放，点 C 在 FD 的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求 CD 的长． 考点：解直角三角形．3797161 分析：过点 B 作 BM⊥FD 于点 M，解直角三角形求出 BC，在△BMC 值解直角三角形求出 CM，BM ，推出 BM=DM，即可求出答案． 解答： 解： 过点 B 作 BM⊥FD 于点 M， 在△ACB 中，∠ACB=90°，∠A=60°，AC=10， ∴∠ABC=30°，BC=AC tan60°=10 ， ∵AB∥CF，∴∠BCM=∠ABC=30°． ∴BM=BC•sin30°=10 × =5 ， CM=BC•cos30°=10 × =15， 在△EFD 中，∠F=90°，∠E=45°， ∴∠EDF=45°， ∴MD=BM=5 ， ∴CD=CM﹣MD=15﹣5 ． 点评：本题考查了解直角三角形的应用，关键是能通过解直角三角形求出线段 CM、MD 的长． 　 24．（10 分）（2011•莆田）如图，将一矩形 OABC 放在直角坐标系中，O 为坐标原点．点 A 在 y 轴正半 轴上．点 E 是边 AB 上的一个动点（不与点 A、B 重合），过点 E 的反比例函数 的图象与 边 BC 交于点 F． （1）若△OAE、△OCF 的面积分别为 S1、S2．且 S1+S2=2，求 k 的值； （2）若 OA=2.0C=4．问当点 E 运动到什么位置时．四边形 OAEF 的面积最大．其最大值为多少？ 考点：反比例函数综合题．3797161 专题：综合题． 分析：（1）设 E（x1， ），F（x2， ），x1＞0，x2＞0，根据三角形的面积公式得到 S1=S2= k ，利用 S1+S2=2 即可求出 k； （2）设 ， ，利用 S 四边形 OAEF=S 矩形 OABC﹣S△BEF﹣S△OCF=﹣ +5，根据二次函数的最值问题即可得到当 k=4 时，四边形 OAEF 的面积有最 大值，S 四边形 OAEF=5，此时 AE=2． 解答：解：（1）∵点 E、F 在函数 y= （x＞0）的图象上， ∴设 E（x1， ），F（x2， ），x1＞0，x2＞0， ∴S1= ，S2= ， ∵S1+S2=2， ∴ =2， ∴k=2； （2）∵四边形 OABC 为矩形，OA=2，OC=4， 设 ， ， ∴BE=4﹣ ，BF=2﹣ ， ∴S△BEF= ﹣k+4， ∵S△OCF= ，S 矩形 OABC=2×4=8， ∴S 四边形 OAEF=S 矩形 OABC﹣S△BEF﹣S△OCF= +4， =﹣ +5， ∴当 k=4 时，S 四边形 OAEF=5， ∴AE=2． 当点 E 运动到 AB 的中点时，四边形 OAEF 的面积最大，最大值是 5． 点评：本题考查了反比例函数 k 的几何含义和点在双曲线上，点的横纵坐标满足反比 例的解析式．也考查了二次的顶点式及其最值问题． 　 25．（10 分）如图，已知⊙O 的直径 AB 与弦 CD 互相垂直，垂足为点 E．⊙O 的切线 BF 与弦 AC 的延 长线相交于点 F，且 AC=8，tan∠BDC= ． （1）求⊙O 的半径长； （2）求线段 CF 长． 考点：切线的性质；垂径定理；解直角三角形．3797161 专题：计算题． 分析：（1）过 O 作 OH 垂直于 AC，利用垂径定理得到 H 为 AC 中点，求出 AH 的长为 4，根据同 弧所对的圆周角相等得到 tanA=tan∠BDC，求出 OH 的长，利用勾股定理即可求出圆的半径 OA 的长； （2）由 AB 垂直于 CD 得到 E 为 CD 的中点，得到 EC=ED，在直角三角形 AEC 中，由 AC 的长以及 tanA 的值求出 CE 与 AE 的长，由 FB 为圆的切线得到 AB 垂直于 BF，得到 CE 与 FB 平行，由平行得比例列出关系式求出 AF 的长，根据 AF﹣AC 即可求出 CF 的长． 解答：解：（1）作 OH⊥AC 于 H，则 AH= AC=4， 在 Rt△AOH 中，AH=4，tanA=tan∠BDC= ， ∴OH=3， ∴半径 OA= =5； （2）∵AB⊥CD， ∴E 为 CD 的中点，即 CE=DE， 在 Rt△AEC 中，AC=8，tanA= ， 设 CE=3k，则 AE=4k， 根据勾股定理得：AC2=CE2+AE2，即 9k2+16k2=64， 解得：k= ， 则 CE=DE= ，AE= ， ∵BF 为圆 O 的切线， ∴FB⊥AB， 又∵AE⊥CD， ∴CE∥FB， ∴ = ，即 = ， 解得：AF= ， 则 CF=AF﹣AC= ． 点评：此题考查了切线的性质，垂径定理，锐角三角函数定义，勾股定理，以及平行线的性质，熟 练掌握切线的性质是解本题的关键． 　 26．（12 分）（2013•江都市模拟）已知 A、B 两地相距 630 千米，在 A、B 之间有汽车站 C 站，如图 1 所示．客车由 A 地驶向 C 站、货车由 B 地驶向 A 地，两车同时出发，匀速行驶，货车的速度是客车速度 的 ．图 2 是客、货车离 C 站的路程 y1、y2（千米）与行驶时间 x（小时）之间的函数关系图象． （1）求客、货两车的速度； （2）求两小时后，货车离 C 站的路程 y2 与行驶时间 x 之间的函数关系式； （3）求 E 点坐标，并说明点 E 的实际意义． 考点：一次函数的应用．3797161 分析：（1）设客车的速度为 a km/h，则货车的速度为 km/h，根据题意列出有关 v 的一元一次方 程解得即可； （2）根据货车两小时到达 C 站，可以设 x 小时到达 C 站，列出关系式即可； （3）两函数的图象相交，说明两辆车相遇，即客车追上了货车． 解答：解：（1）设客车的速度为 a km/h，则货车的速度为 km/h，由题意列方程得： 9a+ ×2=630， 解之，a=60， ∴ =45， 答：客车的速度为 60 km/h，货车的速度为 45km/h （2）方法一：由（1）可知 P（14，540）， ∵D （2，0）， ∴y2=45x﹣90； 方法二：由（1）知，货车的速度为 45km/h， 两小时后货车的行驶时间为（x﹣2）， ∴y2=45（x﹣2）=45x﹣90， （3）方法一：∵F（9，0）M（0，540）， ∴y1=﹣60x+540， 由 ， 解之 ， ∴E （6，180） 点 E 的实际意义：行驶 6 小时时，两车相遇，此时距离 C 站 180km； 方法二：点 E 表示两车离 C 站路程相同，结合题意，两车相遇， 可列方程：45x+60x=630， x=6， ∴540﹣60x=180， ∴E （6，180）， 点评：本题考查了一次函数的应用及一元一次方程的应用，解题的关键是根据题意结合图象说出其 图象表示的实际意义，这样便于理解题意及正确的解题． 　 27．（12 分）如图 1，已知 Rt△ABC 中，∠C=90°，AC=8cm，BC=6cm．点 P 由 B 出发沿 BA 方向向点 A 匀速运动，同时点 Q 由 A 出发沿 AC 方向向点 C 匀速运动，它们的速度均为 2cm/s．以 AQ、PQ 为边作平 行四边形 AQPD，连接 DQ，交 AB 于点 E．设运动的时间为 t（单位：s）（0≤t≤4）．解答下列问题： （1）用含有 t 的代数式表示 AE=　5﹣t　． （2）当 t 为何值时，平行四边形 AQPD 为矩形． （3）如图 2，当 t 为何值时，平行四边形 AQPD 为菱形． 考点：相似形综合题．3797161 分析：（1）首先利用勾股定理求得 AB=10，然后表示出 AP，利用平行四边形对角线互相平分表示 出线段 AE 即可； （2）利用矩形的性质得到△APQ∽△ABC，利用相似三角形对应边的比相等列出比例式即可 求得 t 值； （3）利用菱形的性质得到． 解答：解：（1）∵Rt△ABC 中，∠C=90°，AC=8cm，BC=6cm． ∴由勾股定理得：AB=10cm， ∵点 P 由 B 出发沿 BA 方向向点 A 匀速运动，速度均为 2cm/s， ∴BP=2tcm， ∴AP=AB﹣BP=10﹣2t， ∵四边形 AQPD 为平行四边形， ∴AE= =5﹣t； （2）当▱AQPD 是矩形时，PQ⊥AC， ∴PQ∥BC， ∴△APQ∽△ABC ∴ 即 解之 t= ∴当 t= 时，▱AQPD 是矩形； （3）当▱AQPD 是菱形时，DQ⊥AP， 则 COS∠BAC= = 即 解之 t= ∴当 t= 时，□AQPD 是菱形． 点评：本题考查了相似形的综合知识，正确的利用平行四边形、矩形、菱形的性质得到正方形是解 决本题的关键． 　 28．（14 分）（2012•漳州二模）如图，在平面直角坐标系中，O 是坐标原点，直线 与 x 轴，y 轴分别交于 B，C 两点，抛物线 经过 B，C 两点，与 x 轴的另一个交点为点 A，动点 P 从 点 A 出发沿 AB 以每秒 3 个单位长度的速度向点 B 运动，运动时间为 t（0＜t＜5）秒． （1）求抛物线的解析式及点 A 的坐标； （2）以 OC 为直径的⊙O′与 BC 交于点 M，当 t 为何值时，PM 与⊙O′相切？请说明理由． （3）在点 P 从点 A 出发的同时，动点 Q 从点 B 出发沿 BC 以每秒 3 个单位长度的速度向点 C 运动，动点 N 从点 C 出发沿 CA 以每秒 个单位长度的速度向点 A 运动，运动时间和点 P 相同． ①记△BPQ 的面积为 S，当 t 为何值时，S 最大，最大值是多少？ ②是否存在△NCQ 为直角三角形的情形？若存在，求出相应的 t 值；若不存在，请说明理由． 考点：二次函数综合题．3797161 专题：代数几何综合题；压轴题；动点型． 分析：（1）由直线 与 x 轴，y 轴分别交于 B，C 两点，分别令 x=0 和 y=0 求出 B 与 C 的 坐标，又抛物线经过 B，C 两点，把求出的 B 与 C 的坐标代入到二次函数的表达式里得到关 于 b，c 的方程，联立解出 b 和 c 即可求出二次函数的解析式．又因 A 点是二次函数与 x 轴的 另一交点令 y=0 即可求出点 A 的坐标． （2）连接 OM，PM 与⊙O′相切作为题中的已知条件来做．由直径所对的圆周角为直角可得 ∠OMC=90°从而得∠OMB=90°．又因为 O′O 是⊙O′的半径，O′O⊥OP 得到 OP 为⊙O′的切线， 然后根据从圆外一点引圆的两条切线，切线长相等可得 OP=PM，根据等边对等角得 ∠POM=∠PMO，然后根据等角的余角相等可得∠PMB=∠OBM，再根据等角对等边得 PM=PB， 然后等量代换即可求出 OP 的长，加上 OA 的长即为点 P 运动过的路程 AP，最后根据时间等 于路程除以速度即可求出时间 t 的值． （3）①由路程等于速度乘以时间可知点 P 走过的路程 AP=3t，则 BP=15﹣3t，点 Q 走过的 路程为 BQ=3t，然后过点 Q 作 QD⊥OB 于点 D，证△BQD∽△BCO，由相似得比列即可表示出 QD 的长，然后根据三角形的面积公式即可得到 S 关于 t 的二次函数关系式，然后利用 t=﹣ 时对 应的 S 的值即可求出此时的最大值． ②要使△NCQ 为直角三角形，必须满足三角形中有一个直角，由 BA=BC 可知∠BCA=∠BAC， 所以角 NCQ 不可能为直角，所以分两种情况来讨论：第一种，当角 NQC 为直角时，利用两 组对应角的相等可证△NCQ∽△CAO，由相似得比例即可求出 t 的值；第二种当∠QNC=90°时 ，也是证三角形的相似，由相似得比例求出 t 的值． 解答：解：（1）在 y=﹣ x+9 中，令 x=0，得 y=9；令 y=0，得 x=12． ∴C（0，9），B（12，0）． 又抛物线经过 B，C 两点，∴ ，解得 ∴y=﹣ x2+ x+9． 于是令 y=0，得﹣ x2+ x+9=0， 解得 x1=﹣3，x2=12．∴A（﹣3，0）． （2）当 t=3 秒时，PM 与⊙O′相切．连接 OM． ∵OC 是⊙O′的直径，∴∠OMC=90°．∴∠OMB=90°． ∵O′O 是⊙O′的半径，O′O⊥OP，∴OP 是⊙O′的切线． 而 PM 是⊙O′的切线，∴PM=PO．∴∠POM=∠PMO． 又∵∠POM+∠OBM=90°，∠PMO+∠PMB=90°，∴∠PMB=∠OBM．∴PM=PB． ∴PO=PB= OB=6．∴PA=OA+PO=3+6=9．此时 t=3（秒）． ∴当 t=3 秒，PM 与⊙O′相切． （3）①过点 Q 作 QD⊥OB 于点 D． ∵OC⊥OB，∴QD∥OC．∴△BQD∽△BCO．∴ = ． 又∵OC=9，BQ=3t，BC=15，∴ = ，解得 QD= t． ∴S△BPQ= BP•QD= ．即 S= ． S= ．故当 时，S 最大，最大值为 ． ②存在△NCQ 为直角三角形的情形． ∵BC=BA=15，∴∠BCA=∠BAC，即∠NCM=∠CAO． ∴△NCQ 欲为直角三角形，∠NCQ≠90°，只存在∠NQC=90°和∠QNC=90°两种情况． 当∠NQC=90°时，∠NQC=∠COA=90°，∠NCQ=∠CAO， ∴△NCQ∽△CAO．∴ = ．∴ = ，解得 t= ． 当∠QNC=90°时，∠QNC=∠COA=90°，∠QCN=∠CAO， ∴△QCN∽△CAO．∴ = ．∴ = ，解得 ． 综上，存在△NCQ 为直角三角形的情形，t 的值为 和 ． 点评：本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法， 以及圆的切线的有关性质．在求有关动点问题时要注意分析题意分情况讨论结果． 2017 年中考数学模拟试卷（四） 　 一、选择题（每小题 3 分，满分 24 分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案 的选项填涂在答题卡的相应位置. 1．（3 分）（2012•宜昌）如图，数轴上表示数﹣2 的相反数的点是（　　） 　A．点 P B．点 Q C．点 M D．点 N 考点： 数轴；相反数． 分析： 根据数轴得出 N、M、Q、P 表示的数，求出﹣2 的相反数，根据以上结论即可得出答案． 解答： 解：从数轴可以看出 N 表示的数是﹣2，M 表示的数是﹣0.5，Q 表示的数是 0.5，P 表示的数是 2， ∵﹣2 的相反数是 2， ∴数轴上表示数﹣2 的相反数是点 P， 故选 A． 点评： 本题考查了数轴和相反数的应用，主要培养学生的观察图形的能力和理解能力，题型较好，难度不 大． 　 2．（3 分）（2013•鹤壁二模）已知，如图，AD 与 BC 相交于点 O，AB∥CD，如果∠B=20°，∠D=40°，那 么∠BOD 为（　　） 　A．40° B．50° C．60° D．70° 考点： 平行线的性质． 分析： 由 AB∥CD，∠B=20°，根据两直线平行，内错角相等，即可求得∠C 的度数，又由三角形外角的性质 ，即可求得∠BOD 的度数． 解答： 解：∵AB∥CD，∠B=20°， ∴∠C=∠B=20°， ∵∠D=40°， ∴∠BOD=∠C+∠D=60°． 故选 C． 点评： 此题考查了平行线的性质、三角形外角的性质．此题难度不大，解题的关键是注意掌握两直线平行， 内错角相等定理的应用． 　 3．（3 分）（2012•云南）不等式组 的解集是（　　） 　A．x＜1 B．x＞﹣4 C．﹣4＜x＜1 D．x＞1 考点： 解一元一次不等式组． 分析： 先求出不等式组中每一个不等式的解集，再求出它们的公共部分，即可得到不等式组 的解集． 解答： 解： ， 由①得﹣x＞﹣1，即 x＜1； 由②得 x＞﹣4； 由以上可得﹣4＜x＜1． 故选 C． 点评： 主要考查了一元一次不等式解集的求法，其简便求法就是用口诀求解，求不等式组解集的口诀：同 大取大，同小取小，大小小大中间找，大大小小找不到（无解）． 　 4．（3 分）（2012•六盘水）如图是王老师去公园锻炼及原路返回时离家的距离 y（千米）与时间 t（分钟 ）之间的函数图象，根据图象信息，下列说法正确的是（　　） 　A．王老师去时所用的时间少于回家的时间 　B．王老师在公园锻炼了 40 分钟 　C．王老师去时走上坡路，回家时走下坡路 　D．王老师去时速度比回家时的速度慢 考点： 函数的图象． 专题： 压轴题． 分析： 根据图象可以得到去时所用的时间和回家所用的时间，在公园锻炼了多少分钟，也可以求出去时的 速度和回家的速度，根据可以图象判断去时是否走上坡路，回家时是否走下坡路． 解答： 解：如图， A、王老师去时所用的时间为 15 分钟，回家所用的时间为 5 分钟，故选项错误； B、王老师在公园锻炼了 40﹣15=25 分钟，故选项错误； C、据（1）王老师去时走下坡路，回家时走上坡路，故选项错误． D、王老师去时用了 15 分钟，回家时候用了 5 分钟，因此去时的速度比回家时的速度慢，故选项正 确． 故选 D． 点评： 本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程， 就能够通过图象得到函数问题的相应解决．需注意计算单位的统一． 　 5．（3 分）（2013•鹤壁二模）下列计算正确的是（　　） 　A． B．（x+y）2=x2+y2 C．（﹣3x）3=﹣9x3 D．﹣（x﹣6）=6﹣x 考点： 完全平方公式；实数的运算；去括号与添括号；幂的乘方与积的乘方． 分析： 根据完全平方公式以及积的乘方公式即可判断． 解答： 解：A、不是同类二次根式不能合并，选项错误； B、（x+y）2=x2+2xy+y2，选项错误； C、（﹣3x）3=﹣27x3，选项错误； D、正确． 故选 D． 点评： 本题主要考查完全平方公式，熟记公式结构是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2． 　 6．（3 分）（2012•湛江）一个扇形的圆心角为 60°，它所对的弧长为 2πcm，则这个扇形的半径为（　　） 　A．6cm B．12cm C．2 cm D． cm 考点： 弧长的计算． 专题： 计算题；压轴题． 分析： 由已知的扇形的圆心角为 60°，它所对的弧长为 2πcm，代入弧长公式即可求出半径 R． 解答： 解：由扇形的圆心角为 60°，它所对的弧长为 2πcm， 即 n=60°，l=2π， 根据弧长公式 l= ，得 2π= ， 即 R=6cm． 故选 A． 点评： 此题考查了弧长的计算，解题的关键是熟练掌握弧长公式，理解弧长公式中各个量所代表的意义． 　 7．（3 分）（2013•昭通）已知一组数据：12，5，9，5，14，下列说法不正确的是（　　） 　A．平均数是 9 B．中位数是 9 C．众数是 5 D．极差是 5 考点： 极差；算术平均数；中位数；众数． 分析： 分别计算该组数据的平均数、中位数、众数及极差后即可得到正确的答案． 解答： 解：平均数为（12+5+9+5+14）÷5=9，故 A 正确； 中位数为 9，故 B 正确； 5 出现了 2 次，最多，众数是 5，故 C 正确； 极差为：14﹣5=9，故 D 错误． 故选 D． 点评： 本题考查了数据的平均数、中位数、众数及极差，属于基础题，比较简单． 　 8．（3 分）（2010•长春）如图，平面直角坐标系中，OB 在 x 轴上，∠ABO=90°，点 A 的坐标为（1，2） ，将△AOB 绕点 A 逆时针旋转 90°，点 O 的对应点 C 恰好落在双曲线 y= （x＞0）上，则 k 的值为（　　） 　A．2 B．3 C．4 D．6 考点： 反比例函数图象上点的坐标特征；坐标与图形变化-旋转． 专题： 压轴题． 分析： 由旋转可得点 D 的坐标为（3，2），那么可得到点 C 的坐标为（3，1），那么 k 等于点 C 的横纵坐 标的积． 解答： 解：易得 OB=1，AB=2， ∴AD=2， ∴点 D 的坐标为（3，2）， ∴点 C 的坐标为（3，1）， ∴k=3×1=3． 故选 B． 点评： 解决本题的关键是利用旋转的性质得到在反比例函数上的点 C 的坐标． 　 二、填空题（每小题 3 分，满分 21 分） 9．（3 分）（2012•长沙）若实数 a、b 满足|3a﹣1|+b2=0，则 ab 的值为　1　． 考点： 非负数的性质：偶次方；非负数的性质：绝对值． 分析： 根据非负数的性质列式求出 a、b 的值，然后代入代数式，根据任何非 0 数的 0 次幂等于 1 进行计算 即可得解． 解答： 解：根据题意得，3a﹣1=0，b=0， 解得 a= ，b=0， ab=（ ）0=1． 故答案为：1． 点评： 本题考查了绝对值非负数，平方数非负数的性质，根据几个非负数的和等于 0，则每一个算式都等 于 0 列式是解题的关键． 　 10．（3 分）（2012•湛江）请写出一个二元一次方程组　此题答案不唯一，如： 　，使它的解 是 ． 考点： 二元一次方程组的解． 专题： 压轴题；开放型． 分析： 根据二元一次方程解的定义，可知在求解时，应先围绕 x=2，y=﹣1 列一组算式，然后用 x，y 代换 即可列不同的方程组．答案不唯一，符合题意即可． 解答： 解：此题答案不唯一，如： ， ， ①+②得：2x=4， 解得：x=2， 将 x=2 代入①得：y=﹣1， ∴一个二元一次方程组 的解为： ． 故答案为：此题答案不唯一，如： ． 点评： 本题主要考查了二元一次方程组的解的定义．此题属于开放题，注意正确理解定义是解题的关键． 　 11．（3 分）（2006•泰州）如图，AB，CD 相交于点 O，AB=CD，试添加一个条件使得△AOD≌△COB， 你添加的条件是　AO=CO　．（答案不惟一，只需写一个） 考点： 全等三角形的判定． 专题： 开放型． 分析： 要使△AOD≌△COB，已知 AB=CD，∠AOD=∠COB 所以可以再添加一组边从而利用 SAS 来判定其 全等，可加 AO=CO 或 BO=DO． 解答： 解：若添加 AO=CO ∵AB=CD，AO=CO ∴OD=OB ∵∠AOD=∠COB ∴△AOD≌△COB（SAS）． 故填 AO=CO． 点评： 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL ．添加时注意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与， 若有两边一角对应相等时，角必须是两边的夹角． 　 12．（3 分）（2012•哈尔滨）一个圆锥的母线长为 4，侧面积为 8π，则这个圆锥的底面圆的半径是　2　． 考点： 圆锥的计算． 分析： 根据扇形的面积公式求出扇形的圆心角，再利用弧长公式求出弧长，再利用圆的面积公式求出底面 半径． 解答： 解： 解得 n=180 则弧长= =4π 2πr=4π 解得 r=2 故答案是：2． 点评： 解决本题的关键是根据圆锥的侧面积公式得到圆锥的底面半径的求法． 　 13．（3 分）（2012•攀枝花）如图，正方形 ABCD 中，AB=4，E 是 BC 的中点，点 P 是对角线 AC 上一 动点，则 PE+PB 的最小值为　2 　． 考点： 轴对称-最短路线问题；正方形的性质． 专题： 压轴题；探究型． 分析： 由于点 B 与点 D 关于 AC 对称，所以如果连接 DE，交 AC 于点 P，那 PE+PB 的值最小．在 Rt△CDE 中，由勾股定理先计算出 DE 的长度，即为 PE+PB 的最小值． 解答： 解：连接 DE，交 AC 于点 P，连接 BD． ∵点 B 与点 D 关于 AC 对称， ∴DE 的长即为 PE+PB 的最小值， ∵AB=4，E 是 BC 的中点， ∴CE=2， 在 Rt△CDE 中， DE= = =2 ． 故答案为：2 ． 点评： 本题考查了轴对称﹣最短路线问题和正方形的性质，根据两点之间线段最短，可确定点 P 的位置． 　 14．（3 分）（2013•鹤壁二模）如图，已知二次函数 y=x2+bx+c 的图象经过点（﹣1，0），（1，﹣2）， 该图象与 x 轴的另一个交点为 C，则 AC 长为　3　． 考点： 待定系数法求二次函数解析式；抛物线与 x 轴的交点；两点间的距离． 专题： 计算题． 分析： 先把点（﹣1，0），（1，﹣2）代入 y=x2+bx+c，求得 b，c，再令 y=0，点 C 的坐标，再得出答案 即可． 解答： 解：∵二次函数 y=x2+bx+c 的图象经过点（﹣1，0），（1，﹣2）， ∴ ， 解得 ， ∴抛物线的解析式为 y=x2﹣x﹣2， 令 y=0，得 x2﹣x﹣2=0， 解得 x1=﹣1，x2=2， ∴C（2，0） ∴AC=2﹣（﹣1）=3． 故答案为 3． 点评： 本题考查了用待定系数法求二次函数的解析式、抛物线与 x 轴的交点问题以及两点间距离的求法， 是基础知识要熟练掌握． 　 15．（3 分）（2011•安顺）已知：如图，O 为坐标原点，四边形 OABC 为矩形，A（10，0），C（0，4） ，点 D 是 OA 的中点，点 P 在 BC 上运动，当△ODP 是腰长为 5 的等腰三角形时，则 P 点的坐标为　（2， 4）或（3，4）或（8，4）　． 考点： 矩形的性质；坐标与图形性质；等腰三角形的性质． 专题： 压轴题；数形结合． 分析： 分 PD=OD（P 在右边），PD=OD（P 在左边），OP=OD 三种情况，根据题意画出图形，作 PQ 垂 直于 x 轴，找出直角三角形，根据勾股定理求出 OQ，然后根据图形写出 P 的坐标即可． 解答： 解：当 OD=PD（P 在右边）时，根据题意画出图形，如图所示： 过 P 作 PQ⊥x 轴交 x 轴于 Q，在直角三角形 DPQ 中，PQ=4，PD=OD= OA=5， 根据勾股定理得：DQ=3，故 OQ=OD+DQ=5+3=8，则 P1（8，4）； 当 PD=OD（P 在左边）时，根据题意画出图形，如图所示： 过 P 作 PQ⊥x 轴交 x 轴于 Q，在直角三角形 DPQ 中，PQ=4，PD=OD=5， 根据勾股定理得：QD=3，故 OQ=OD﹣QD=5﹣3=2，则 P2（2，4）； 当 PO=OD 时，根据题意画出图形，如图所示： 过 P 作 PQ⊥x 轴交 x 轴于 Q，在直角三角形 OPQ 中，OP=OD=5，PQ=4， 根据勾股定理得：OQ=3，则 P3（3，4）， 综上，满足题意的 P 坐标为（2，4）或（3，4）或（8，4）． 故答案为：（2，4）或（3，4）或（8，4） 点评： 这是一道代数与几何知识综合的开放型题，综合考查了等腰三角形和勾股定理的应用，属于策略和 结果的开放，这类问题的解决方法是：数形结合，依理构图解决问题． 　 三、解答题（本大题共 8 个小题，满分 75 分） 16．（8 分）（2013•鹤壁二模）已知[（x﹣y）2﹣（x+y）2+y（2x﹣y）]÷（﹣2y）=2，求 的值． 考点： 分式的化简求值；整式的除法． 分析： 先把所求代数式进行化简，再根据题意求出 2x+y 的值，代入所求代数式进行计算即可． 解答： 解：原式= ﹣ = ∵[（x﹣y）2﹣（x+y）2+y（2x﹣y）]÷（﹣2y）=2， ∴2x+y=4． ∴原式= = = ． 点评： 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键． 　 17．（9 分）（2013•鹤壁二模）已知：如图，在等腰梯形 ABCD 中，AD∥BC，∠BDC=∠BCD，点 E 是线 段 BD 上一点，且 BE=AD． （1）证明：△ADB≌△EBC； （2）直接写出图中所有的等腰三角形． 考点： 等腰梯形的性质；全等三角形的判定与性质；等腰三角形的判定． 分析： （1）根据平行线的性质判定∠ADB=∠EBC，然后由∠BDC=∠BCD，得出 BD=BC，结合 BE=AD，利 用 SAS 可证明结论； （2）根据（1）的结论，可得 CE=AB，结合等腰梯形的性质，可写出等腰三角形． 解答： 解（1）∵AD∥BC， ∴∠ADB=∠EBC， ∵∠BDC=∠BCD， ∴BD=BC， 在△ADB 和△EBC 中， ∴△ADB≌△EBC（SAS）．（2）由（1）可得△BCD 是等腰三角形； ∵△ADB≌△EBC， ∴CE=AB， 又∵AB=CD， ∴CE=CD， ∴△CDE 是等腰三角形． 点评： 本题考查了等腰三角形的性质及判定，等腰梯形的性质，解答本题的关键是掌握全等三角形的判定 定理及等腰梯形的性质，难度一般． 　 18．（9 分）（2013•鹤壁二模）已知，如图，在坡顶 A 处的同一水平面上有一座古塔 BC，数学兴趣小组 的同学在斜坡底 P 处测得该塔的塔顶 B 的仰角为 45°，然后他们沿着坡度为 1：2.4 的斜坡 AP 攀行了 26 米 ，在坡顶 A 处又测得该塔的塔顶 B 的仰角为 76°．求： （1）坡顶 A 到地面 PQ 的距离； （2）古塔 BC 的高度（结果精确到 1 米）． （参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01） 考点： 解直角三角形的应用-仰角俯角问题． 分析： （1）先过点 A 作 AH⊥PO，根据斜坡 AP 的坡度为 1：2.4，得出 = ，设 AH=5k，则 PH=12k， AP=13k，求出 k 的值即可． （2）先延长 BC 交 PO 于点 D，根据 BC⊥AC，AC∥PO，得出 BD⊥PO，四边形 AHDC 是矩形，再 根据∠BPD=45°，得出 PD=BD，然后设 BC=x，得出 AC=DH=x﹣14，最后根据在 Rt△ABC 中， tan76°= ，列出方程，求出 x 的值即可． 解答： 解：（1）过点 A 作 AH⊥PO，垂足为点 H， ∵斜坡 AP 的坡度为 1：2.4， ∴ = ， 设 AH=5k，则 PH=12k，由勾股定理，得 AP=13k， ∴13k=26， 解得 k=2， ∴AH=10， 答：坡顶 A 到地面 PQ 的距离为 10 米． （2）延长 BC 交 PO 于点 D， ∵BC⊥AC，AC∥PO， ∴BD⊥PO， ∴四边形 AHDC 是矩形，CD=AH=10，AC=DH， ∵∠BPD=45°， ∴PD=BD， 设 BC=x，则 x+10=24+DH， ∴AC=DH=x﹣14， 在 Rt△ABC 中，tan76°= ，即 ≈4.01． 解得 x≈19． 答：古塔 BC 的高度约为 19 米． 点评： 此题考查了解直角三角形，用到的知识点是勾股定理、锐角三角函数、坡角与坡角等，关键是做出 辅助线，构造直角三角形． 　 19．（9 分）（2009•黔南州）“农民也可以报销医疗费了！”这是某市推行新型农村医疗合作的成果．村民 只要每人每年交 10 元钱，就可以加入合作医疗，每年先由自己支付医疗费，年终时可得到按一定比例返 回的返回款．这一举措极大地增强了农民抵御大病风险的能力．小华与同学随机调查了他们乡的一些农民 ，根据收集到的数据绘制了以下的统计图． 根据以上信息，解答以下问题： （1）本次调查了多少村民，被调查的村民中，有多少人参加合作医疗得到了返回款； （2）该乡若有 10 000 村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到 9 680 人，假设这两年的年增长率相同，求这个年增长率． 考点： 扇形统计图；一元二次方程的应用；用样本估计总体；条形统计图． 专题： 阅读型；图表型． 分析： （1）根据样本容量为各组频数之和，可得共有 240+60=300（人）；其中有 2.5%即 6 人得到了返回 款； （2）用样本估计总体即可得出答案． 解答： 解：（1）调查的村民数=240+60=300 人， 参加合作医疗得到了返回款的人数=240×2.5%=6 人；（2）∵参加医疗合作的百分率为 =80%， ∴估计该乡参加合作医疗的村民有 10000×80%=8000 人， 设年增长率为 x，由题意知 8000×（1+x）2=9680， 解得：x1=0.1，x2=﹣2.1（舍去）， 即年增长率为 10%． 答：共调查了 300 人，得到返回款的村民有 6 人，估计有 8000 人参加了合作医疗，年增长率为 10%． 点评： 本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信 息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图中各部分占总体的 百分比之和为 1，直接反映部分占总体的百分比大小． 　 20．（9 分）（2012•六盘水）假期，六盘水市教育局组织部分教师分别到 A、B、C、D 四个地方进行新 课程培训，教育局按定额购买了前往四地的车票．如图 1 是未制作完成的车票种类和数量的条形统计图， 请根据统计图回答下列问题： （1）若去 C 地的车票占全部车票的 30%，则去 C 地的车票数量是　30　张，补全统计图． （2）若教育局采用随机抽取的方式分发车票，每人一张（所有车票的形状、大小、质地完全相同且充分 洗匀），那么余老师抽到去 B 地的概率是多少？ （3）若有一张去 A 地的车票，张老师和李老师都想要，决定采取旋转转盘的方式来确定．其中甲转盘被 分成四等份且标有数字 1、2、3、4，乙转盘分成三等份且标有数字 7、8、9，如图 2 所示．具体规定是： 同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给李老师，否则票给张老师（指针指在线上 重转）．试用“列表法”或“树状图”的方法分析这个规定对双方是否公平． 考点： 游戏公平性；扇形统计图；条形统计图；概率公式；列表法与树状图法． 分析： （1）根据去 A、B、D 的车票总数除以所占的百分比求出总数，再减去去 A、B、D 的车票总数即 可； （2）用去 B 地的车票数除以总的车票数即可； （3）根据题意用列表法分别求出当指针指向的两个数字之和是偶数时的概率，即可求出这个规定对 双方是否公平． 解答： 解：（1）根据题意得： 总的车票数是：（20+40+10）÷（1﹣30%）=100， 则去 C 地的车票数量是 100﹣70=30； 故答案为：30．（2）余老师抽到去 B 地的概率是 = ；（3）根据题意列表如下： 因为两个数字之和是偶数时的概率是 = ， 所以票给李老师的概率是 ， 所以这个规定对双方公平． 点评： 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否 则就不公平． 　 21．（10 分）（2010•眉山）某渔场计划购买甲、乙两种鱼苗共 6000 尾，甲种鱼苗每尾 0.5 元，乙种鱼苗 每尾 0.8 元．相关资料表明：甲、乙两种鱼苗的成活率分别为 90%和 95%． （1）若购买这批鱼苗共用了 3600 元，求甲、乙两种鱼苗各购买了多少尾？ （2）若购买这批鱼苗的钱不超过 4200 元，应如何选购鱼苗？ （3）若要使这批鱼苗的成活率不低于 93%，且购买鱼苗的总费用最低，应如何选购鱼苗？ 考点： 一元一次不等式的应用；一次函数的应用． 专题： 压轴题． 分析： （1）0.5×甲种鱼的尾数+0.8×乙种鱼的尾数=3600； （2）0.5×甲种鱼的尾数+0.8×乙种鱼的尾数≤4200； （3）关系式为：甲种鱼的尾数×0.9+乙种鱼的尾数×95%≥6000×93%． 解答： 解：（1）设购买甲种鱼苗 x 尾，则购买乙种鱼苗（6000﹣x）尾． 由题意得：0.5x+0.8（6000﹣x）=3600， 解这个方程，得：x=4000， ∴6000﹣x=2000， 答：甲种鱼苗买 4000 尾，乙种鱼苗买 2000 尾；（2）由题意得：0.5x+0.8（6000﹣x）≤4200， 解这个不等式，得：x≥2000， 即购买甲种鱼苗应不少于 2000 尾，乙不超过 4000 尾；（3）设购买鱼苗的总费用为 y，甲种鱼苗买 了 x 尾． 则 y=0.5x+0.8（6000﹣x）=﹣0.3x+4800， 由题意，有 x+ （6000﹣x）≥ ×6000， 解得：x≤2400， 在 y=﹣0.3x+4800 中， ∵﹣0.3＜0，∴y 随 x 的增大而减少， ∴当 x=2400 时，y 最小=4080． 答：购买甲种鱼苗 2400 尾，乙种鱼苗 3600 尾时，总费用最低． 点评： 根据钱数和成活率找到相应的关系式是解决本题的关键，注意不低于是大于或等于；不超过是小于 或等于． 　 22．（10 分）（2013•鹤壁二模）如图，在梯形 ABCD 中，AD∥BC，∠ABC=90°，DG⊥BC 于 G，BH⊥DC 于 H，CH=DH，点 E 在 AB 上，点 F 在 BC 上，并且 EF∥DC． （1）若 AD=3，CG=2，求 CD； （2）若 CF=AD+BF，求证：EF= CD． 考点： 直角梯形；勾股定理；矩形的性质；相似三角形的判定与性质． 专题： 几何综合题；压轴题． 分析： （1）由 AD∥BC，∠ABC=90°，DG⊥BC 得到四边形 ABGD 为矩形，利用矩形的性质有 AD=BG=3， AB=DG，而 BH⊥DC，CH=DH，根据等腰三角形的判定得到△BDC 为等腰三角形，即有 BD=BG+GC=3+2=5，先在 Rt△ABD 中求出 AB，然后在 Rt△DGC 中求出 DC； （2）由 CF=AD+BF，AD=BG，经过线段代换易得 GC=2BF，再由 EF∥DC 得到∠BFE=∠GCD，根据 三角形相似的判定易得 Rt△BEF∽Rt△GDC，利用相似比即可得到结论． 解答： （1）解：连 BD，如图， ∵在梯形 ABCD 中，AD∥BC，∠ABC=90°，DG⊥BC， ∴四边形 ABGD 为矩形， ∴AD=BG=3，AB=DG， 又∵BH⊥DC，CH=DH， ∴△BDC 为等腰三角形， ∴BD=BG+GC=3+2=5， 在 Rt△ABD 中，AB= = =4， ∴DG=4， 在 Rt△DGC 中， ∴DC= = =2 ．（2）证明：∵CF=AD+BF， ∴CF=BG+BF， ∴FG+GC=BF+FG+BF，即 GC=2BF， ∵EF∥DC， ∴∠BFE=∠GCD， ∴Rt△BEF∽Rt△GDC， ∴EF：DC=BF：GC=1：2， ∴EF= DC． 点评： 本题考查了直角梯形的性质：有一组对边平行，另一组对边不平行，且有一个直角．也考查了矩形 的性质、勾股定理、等腰三角形的判定以及相似三角形的判定与性质． 　 23．（11 分）（2007•河池）如图，四边形 OABC 为直角梯形，A（4，0），B（3，4），C（0，4）．点 M 从 O 出发以每秒 2 个单位长度的速度向 A 运动；点 N 从 B 同时出发，以每秒 1 个单位长度的速度向 C 运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点 N 作 NP 垂直 x 轴于点 P，连接 AC 交 NP 于 Q，连接 MQ． （1）点　M　（填 M 或 N）能到达终点； （2）求△AQM 的面积 S 与运动时间 t 的函数关系式，并写出自变量 t 的取值范围，当 t 为何值时，S 的值 最大； （3）是否存在点 M，使得△AQM 为直角三角形？若存在，求出点 M 的坐标；若不存在，说明理由． 考点： 二次函数综合题． 专题： 压轴题． 分析： （1）（BC÷点 N 的运动速度）与（OA÷点 M 的运动速度）可知点 M 能到达终点． （2）经过 t 秒时可得 NB=y，OM﹣2t．根据∠BCA=∠MAQ=45°推出 QN=CN，PQ 的值．求出 S 与 t 的函数关系式后根据 t 的值求出 S 的最大值． （3）本题分两种情况讨论（若∠AQM=90°，PQ 是等腰 Rt△MQA 底边 MA 上的高；若∠QMA=90°， QM 与 QP 重合）求出 t 值． 解答： 解：（1）点 M．（1 分）（2）经过 t 秒时，NB=t，OM=2t， 则 CN=3﹣t，AM=4﹣2t， ∵∠BCA=∠MAQ=45°， ∴QN=CN=3﹣t ∴PQ=1+t，（2 分） ∴S△AMQ= AM•PQ= （4﹣2t）（1+t）=﹣t2+t+2．（3 分） ∴S=﹣t2+t+2=﹣t2+t﹣ + +2=﹣（t﹣ ）2+ ，（5 分） ∵0≤t＜2 ∴当 时，S 的值最大．（6 分）（3）存在．（7 分） 设经过 t 秒时，NB=t，OM=2t 则 CN=3﹣t，AM=4﹣2t ∴∠BCA=∠MAQ=45°（8 分） ①若∠AQM=90°，则 PQ 是等腰 Rt△MQA 底边 MA 上的高 ∴PQ 是底边 MA 的中线 ∴PQ=AP= MA ∴1+t= （4﹣2t） ∴t= ∴点 M 的坐标为（1，0）（10 分） ②若∠QMA=90°，此时 QM 与 QP 重合 ∴QM=QP=MA ∴1+t=4﹣2t ∴t=1 ∴点 M 的坐标为（2，0）．（12 分） 点评： 本题考查的是二次函数的有关知识，考生还需注意的是要学会全面分析问题的可行性继而解答． 　 2017 年中考数学模拟试卷（五） 　 一、选择题（本大题共 10 题，每小题 3 分，共 30 分）在每小题列出的四个选项中，只有一个是正确的， 请将正确选项的字母写在答卷相应的位置上． 1．（3 分）（2012•衢州）下列四个数中，最小的数是（　　） 　A．2 B．﹣2 C．0 D．﹣ 考点： 有理数大小比较． 专题： 探究型． 分析： 根据有理数比较大小的法则进行比较即可． 解答： 解：∵2＞0，﹣2＜0，﹣ ＜0， ∴可排除 A、C， ∵|﹣2|=2，|﹣ |= ，2＞ ， ∴﹣2＜﹣ ． 故选 B． 点评： 本题考查的是有理数的大小比较，熟知正数都大于 0； 负数都小于 0； 正数大于一切负数； 两个 负数，绝对值大的其值反而小是解答此题的关键． 　 2．（3 分）（2013•潮安县模拟）2012 年广东省人口数超过 104000000，将 104000000 这个数用科学记数 法表示为（　　） 　A．0.104×109 B．1.04×109 C．1.04×108 D．104×106 考点： 科学记数法—表示较大的数． 分析： 科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值是易错点，由于 104000000 有 9 位，所以可以确定 n=9﹣1=8． 解答： 解：104 000 000=1.04×108． 故选 C． 点评： 此题考查科学记数法表示较大的数的方法，准确确定 a 与 n 值是关键． 　 3．（3 分）（2013•潮安县模拟）在下列运算中，计算正确的是（　　） 　A．a2+a2=a4 B．a3•a2=a6 C．a8÷a2=a4 D．（a2）3=a6 考点： 同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方． 专题： 计算题． 分析： A、原式不能合并，错误； B、原式利用同底数幂的乘法法则计算得到结果，即可做出判断； C、原式利用同底数幂的除法法则计算得到结果，即可做出判断； D、原式利用幂的乘方运算法则计算得到结果，即可做出判断． 解答： 解：A、a2+a2=2a2，本选项错误； B、a3•a2=a5，本选项错误； C、a8÷a2=a6，本选项错误； D、（a2）3=a6，本选项正确． 故选 D． 点评： 此题考查了同底数幂的乘除法，合并同类项，以及幂的乘方与积的乘方，熟练掌握运算法则是解本 题的关键． 　 4．（3 分）（2013•潮安县模拟）函数 的自变量 x 的取值范围是（　　） 　A．x＞0 B．x≥0 C．x＞1 D．x≠1 考点： 函数自变量的取值范围． 分析： 根据被开方数大于等于 0，分母不等于 0 列式计算即可得解． 解答： 解：根据题意得，x﹣1＞0， 解得 x＞1． 故选 C． 点评： 本题考查了函数自变量的范围，一般从三个方面考虑： （1）当函数表达式是整式时，自变量可取全体实数； （2）当函数表达式是分式时，考虑分式的分母不能为 0； （3）当函数表达式是二次根式时，被开方数非负． 　 5．（3 分）（2001•陕西）下列图形中，既是轴对称图形又是中心对称图形的是（　　） 　A．矩形 B．平行四边形 C．等腰梯形 D．等腰三角形 考点： 轴对称图形；中心对称图形． 分析： 根据轴对称图形与中心对称图形的概念结合矩形、平行四边形、等腰梯形、等腰三角形的性质求解． 解答： 解：A、是轴对称图形，也是中心对称图形．故正确； B、不是轴对称图形，是中心对称图形．故错误； C、是轴对称图形，不是中心对称图形．故错误； D、是轴对称图形，不是中心对称图形．故错误． 故选 A． 点评： 考查了轴对称图形和中心对称图形的概念． 轴对称图形的关键是寻找对称轴，图形沿对称轴折叠后可重合； 中心对称图形是要寻找对称中心，图形旋转 180°后与原图形重合． 　 6．（3 分）（2013•潮安县模拟）如图，△ABC 中，已知 AB=8，∠C=90°，∠A=30°，DE 是中位线，则 DE 的长为（　　） 　A．4 B．3 C． D．2 考点： 三角形中位线定理；含 30 度角的直角三角形． 分析： 先由含 30°角的直角三角形的性质，得出 BC，再由三角形的中位线定理得出 DE 即可． 解答： 解：∵∠C=90°，∠A=30°， ∴BC= AB=4， 又∵DE 是中位线， ∴DE= BC=2． 故选 D． 点评： 本题考查了三角形的中位线定理，解答本题的关键是掌握含 30°角的直角三角形的性质及三角形的中 位线定理． 　 7．（3 分）（1999•南京）甲、乙两班参加植树造林，已知甲班每天比乙班每天多植 5 棵树，甲班植 80 棵 树所用的天数与乙班植 70 棵树所用的天数相等，若设甲班每天植 x 棵，根据题意列出的方程是（　　） 　A． B． C． D． 考点： 由实际问题抽象出分式方程． 专题： 应用题；压轴题． 分析： 关键描述语是：“甲班植 80 棵树所用的天数比与乙班植 70 棵树所用的天数相等”；等量关系为：甲 班植 80 棵树所用的天数=乙班植 70 棵树所用的天数． 解答： 解：若设甲班每天植 x 棵，那么甲班植 80 棵树所用的天数应该表示为： ，乙班植 70 棵树所用的 天数应该表示为： ．所列方程为： ．故选 D． 点评： 列方程解应用题的关键步骤在于找相等关系．本题应该抓住“甲班植 80 棵树所用的天数比与乙班植 70 棵树所用的天数相等”的关键语． 　 8．（3 分）（2012•衢州）长方体的主视图、俯视图如图所示，则其左视图面积为（　　） 　A．3 B．4 C．12 D．16 考点： 由三视图判断几何体． 分析： 根据物体的主视图与俯视图可以得出，物体的长与高以及长与宽，进而得出左视图面积=宽×高． 解答： 解：由主视图易得高为 1，由俯视图易得宽为 3． 则左视图面积=1×3=3， 故选：A． 点评： 此题主要考查了由三视图判断几何体的形状，利用主视图确定物体的长与高；俯视图确定物体的长 与宽是解题关键． 　 9．（3 分）（2012•济南）暑假即将来临，小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区 参加综合实践活动，那么小明和小亮选到同一社区参加实践活动的概率为（　　） 　A． B． C． D． 考点： 列表法与树状图法． 分析： 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与小明和小亮选到同一社区参加实 践活动的情况，再利用概率公式即可求得答案． 解答： 解：画树状图得： ∵共有 9 种等可能的结果，小明和小亮选到同一社区参加实践活动的有 3 种情况， ∴小明和小亮选到同一社区参加实践活动的概率为： = ． 故选 B． 点评： 此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可 能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所 求情况数与总情况数之比． 　 10．（3 分）（2013•潮安县模拟）如图所示，边长为 1 的小正方形构成的网格中，半径为 1 的⊙O 的圆心 O 在格点上，则∠AED 的正切值等于（　　） 　A． B． C．2 D． 考点： 圆周角定理；锐角三角函数的定义． 专题： 网格型． 分析： 根据同弧或等弧所对的圆周角相等来求解． 解答： 解：∵∠E=∠ABD， ∴tan∠AED=tan∠ABD= = ． 故选 D． 点评： 本题利用了圆周角定理（同弧或等弧所对的圆周角相等）和正切的概念求解． 　 二、填空题（本大题共 6 小题，每小题 4 分，共 24 分）请将下列各题的正确答案填写在答卷相应的位置 上 11．（4 分）（2013•潮安县模拟）“12315”是消费者权益保护投诉电话号码，数据 1、2、3、1、5 中，中 位数是　2　． 考点： 中位数． 分析： 找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数． 解答： 解：题目中数据共有 5 个， 按从小到大排列为 1，1，2，3，5， 故中位数是按从小到大排列后第三个数作为中位数， 故这组数据的中位数是 2． 故答案为 2． 点评： 本题属于基础题，考查了确定一组数据的中位数的能力．要明确定义．一些学生往往对这个概念掌 握不清楚，计算方法不明确而做错．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶 数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数 的平均数． 　 12．（4 分）（2007•河池）分解因式：2x2﹣4xy+2y2=　2（x﹣y）2　． 考点： 提公因式法与公式法的综合运用． 分析： 先提取公因式 2，再对余下的多项式利用完全平方公式继续分解． 解答： 解：2x2﹣4xy+2y2， =2（x2﹣2xy+y2）， =2（x﹣y）2． 点评： 本题考查了提公因式法，公式法分解因式，提取公因式后再利用完全平方公式进行二次因式分解， 分解因式要彻底． 　 13．（4 分）（2013•潮安县模拟）如果 与（2x﹣4）2 互为相反数，那么 2x﹣y=　1　． 考点： 非负数的性质：算术平方根；非负数的性质：偶次方． 分析： 根据互为相反数的两个数的和等于 0 列出等式，再根据非负数的性质列式求出 x、y 的值，然后代入 代数式进行计算即可得解． 解答： 解：∵ 与（2x﹣4）2 互为相反数， ∴ +（2x﹣4）2=0， ∴y﹣3=0，2x﹣4=0， 解得 x=2，y=3， ∴2x﹣y=2×2﹣3=4﹣3=1． 故答案为：1． 点评： 本题考查了非负数的性质：几个非负数的和为 0 时，这几个非负数都为 0． 　 14．（4 分）（2013•潮安县模拟）如图，现有一圆心角为 90°，半径为 8cm 的扇形纸片，用它恰好围成一 个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为　2　cm． 考点： 弧长的计算． 分析： 本题的关键是利用弧长公式计算弧长，再利用底面周长=展开图的弧长可得． 解答： 解：L= =2πR， 解 R=2cm． 点评： 解答本题的关键是有确定底面周长=展开图的弧长这个等量关系，然后由扇形的弧长公式和圆的周长 公式求值． 　 15．（4 分）（2013•潮安县模拟）如图，A（4，0），B（3，3），以 AO，AB 为边作平行四边形 OABC ，则经过 C 点的反比例函数的解析式为　y=﹣ 　． 考点： 待定系数法求反比例函数解析式；平行四边形的性质． 专题： 计算题；待定系数法． 分析： 设经过 C 点的反比例函数的解析式是 y= （k≠0），设 C（x，y）．根据平行四边形的性质求出点 C 的坐标（﹣1，3）．然后利用待定系数法求反比例函数的解析式． 解答： 解：设经过 C 点的反比例函数的解析式是 y= （k≠0），设 C（x，y）． ∵四边形 OABC 是平行四边形， ∴BC∥OA，BC=OA； ∵A（4，0），B（3，3）， ∴点 C 的纵坐标是 y=3，|3﹣x|=4（x＜0）， ∴x=﹣1， ∴C（﹣1，3）． ∵点 C 在反比例函数 y= （k≠0）的图象上， ∴3= ， 解得，k=﹣3， ∴经过 C 点的反比例函数的解析式是 y=﹣ ． 故答案是：y=﹣ ． 点评： 本题主要考查了平行四边形的性质（对边平行且相等）、利用待定系数法求反比例函数的解析式． 解答反比例函数的解析式时，还借用了反比例函数图象上点的坐标特征，经过函数的某点一定在函 数的图象上． 　 16．（4 分）（2013•潮安县模拟）如图（1）是四边形纸片 ABCD，其中∠B=120°，∠D=50 度．若将其右 下角向内折出△PCR，恰使 CP∥AB，RC∥AD，如图（2）所示，则∠C=　95　度． 考点： 翻折变换（折叠问题）． 分析： 根据折叠前后图形全等和平行线，先求出∠CPR 和∠CRP，再根据三角形内角和定理即可求出∠C． 解答： 解：因为折叠前后两个图形全等，故∠CPR= ∠B= ×120°=60°， ∠CRP= ∠D= ×50°=25°； ∴∠C=180°﹣25°﹣60°=95°；∠C=95 度； 故应填 95． 点评： 折叠前后图形全等是解决折叠问题的关键． 　 三、解答题（一）（本大题共 3 小题，每小题 5 分，共 15 分） 17．（5 分）（2012•衢州）计算：|﹣2|+2﹣1﹣cos60°﹣（1﹣ ）0． 考点： 实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值． 分析： 根据零指数幂、负整数指数幂以及特殊角的三角函数值的运算规律计算即可． 解答： 解：原式=2+ ﹣ ﹣1 =2﹣1 =1． 点评： 此题考查了实数的运算、零指数幂、特殊角的三角函数值，属于基础题，解答本题的关键是熟练每 部分的运算法则． 　 18．（5 分）（2013•潮安县模拟）先化简，再求值： ，其中 ． 考点： 分式的化简求值；约分；分式的乘除法；分式的加减法． 专题： 计算题． 分析： 先算括号里面的减法，再把除法变成乘法，进行约分即可． 解答： 解：原式= ÷（ ） = × = ， 当 x= ﹣3 时， 原式= = ． 点评： 本题主要考查对分式的加减、乘除，约分等知识点的理解和掌握，能熟练地运用法则进行化简是解 此题的关键． 　 19．（5 分）（2013•潮安县模拟）解不等式组： ，并把解集在数轴上表示出来． 考点： 解一元一次不等式组；在数轴上表示不等式的解集． 专题： 计算题． 分析： 分别解两个不等式得到 x≥﹣2 和 x＜1，再根据大于小的小于大的取中间确定不等式组的解集，然后 用数轴表示解集． 解答： 解： ， 由①得：x≥﹣2， 由②得：x＜1， ∴不等式组的解集为：﹣2≤x＜1， 如图，在数轴上表示为： ． 点评： 本题考查了解一元一次不等式组：分别求出不等式组各不等式的解集，然后根据“同大取大，同小取 小，大于小的小于大的取中间，大于大的小于小的无解”确定不等式组的解集．也考查了在数轴上表 示不等式的解集． 　 四、解答题（二）（本大题共 3 小题，每小题 8 分，共 24 分） 20．（8 分）（2007•梅州）如图，AC 是平行四边形 ABCD 的对角线． （1）请按如下步骤在图中完成作图（保留作图痕迹）： ①分别以 A，C 为圆心，以大于 AC 长为半径画弧，弧在 AC 两侧的交点分别为 P，Q． ②连接 PQ，PQ 分别与 AB，AC，CD 交于点 E，O，F； （2）求证：AE=CF． 考点： 平行四边形的性质；全等三角形的判定与性质；线段垂直平分线的性质． 专题： 作图题． 分析： （1）熟练用尺规作一条线段的垂直平分线； （2）根据所作的是线段的垂直平分线结合平行四边形的性质，根据 ASA 证明三角形全等．再根据 全等三角形的性质进行证明． 解答： 解：（1）作图，（2）证明：根据作图知，PQ 是 AC 的垂直平分线， ∴AO=CO，且 EF⊥AC． ∵四边形 ABCD 是平行四边形 ∴∠OAE=∠OCF． ∴△OAE≌△OCF（ASA）． ∴AE=CF． 点评： 掌握尺规作图的方法，作图中的条件就是第二问中的已知条件，正确进行尺规作图是解题的关键． 　 21．（8 分）（2013•潮安县模拟）某市 2012 年国民经济和社会发展统计公报显示，2012 年该市新开工的 住房有商品房、廉租房、经济适用房和公共租赁房四种类型．老王对这四种新开工的住房套数和比例进行 了统计，并将统计结果绘制成下面两幅统计图，请你结合图中所给信息解答下列问题： （1）求经济适用房的套数，并补全图 1； （2）假如申请购买经济适用房的对象中共有 950 人符合购买条件，老王是其中之一．由于购买人数超过 房子套数，购买者必须通过电脑摇号产生．如果对 2012 年新开工的经济适用房进行电脑摇号，那么老王 被摇中的概率是多少？ （3）如果计划 2014 年新开工廉租房建设的套数要达到 720 套，那么 2013～2014 这两年新开工廉租房的 套数的年平均增长率是多少？ 考点： 一元二次方程的应用；扇形统计图；条形统计图；概率公式． 分析： 1）根据扇形统计图中公租房所占比例以及条形图中公租房数量即可得出，衢州市新开工的住房总数 ，进而得出经济适用房的套数； （2）根据申请购买经济适用房共有 950 人符合购买条件，经济适用房总套数为 475 套，得出老王被 摇中的概率即可； （3）根据 2012 年廉租房共有 6250×8%=500 套，得出 500（1+x）2=720，即可得出答案． 解答： 解：（1）1500÷24%=6250 6250×7.6%=475 所以经济适用房的套数有 475 套； 如图所示： （2）老王被摇中的概率为： ； （3）设 2013～2014 这两年新开工廉租房的套数的年平均增长率为 x 因为 2012 年廉租房共有 6250×8%=500（套） 所以依题意，得 500（1+x）2=720…（7 分） 解这个方程得，x1=0.2，x2=﹣2.2（不合题意，舍去） 答：这两年新开工廉租房的套数的年平均增长率为 20%． 点评： 此题主要考查了扇形图与条形图的综合应用，根据已知得出新开工的住房总数是解题关键． 　 22．（8 分）（2013•潮安县模拟）如图，⊙M 与 x 轴相切于点 C，与 y 轴的一个交点为 A． （1）求证：AC 平分∠OAM； （2）如果⊙M 的半径等于 4，∠ACO=30°，求 AM 所在直线的解析式． 考点： 圆的综合题． 分析： （1）连结 MC，则 MC⊥x 轴，MC∥y 轴，得出∠MCA=∠OAC，再根据 MA=MC，得出∠MCA=∠MAC ，∠OAC=∠MAC 即可， （2）先证出△MAC 是等边三角形得出 AC=MC=4，求出在 Rt△AOC 中，OA=2，得出 A 点的坐标， 再根据 OC= 求出 OC，得 M 点的坐标，最后设 AM 所在直线的解析式为 y=kx+b，把 A 、B 点的坐标代入计算即可． 解答： （1）证明：∵圆 M 与 x 轴相切于点 C 连结 MC，则 MC⊥x 轴， ∴MC∥y 轴， ∴∠MCA=∠OAC， 又∵MA=MC， ∴∠MCA=∠MAC， ∴∠OAC=∠MAC 即 AC 平分∠OAM； （2）解：∵∠ACO=30°， ∴∠MCA=60°， ∴△MAC 是等边三角形 ∴AC=MC=4 ∴在 Rt△AOC 中，OA=2 即 A 点的坐标是（0，2）， 又∵OC= = =2 ， ∴M 点的坐标是（ ，4）， 设 AM 所在直线的解析式为 y=kx+b 则 ， 解得 k= ，b=2 ∴AM 所在直线的解析式为 y= x+2． 点评： 此题考查了圆的综合，用到的知识点是切线的性质、勾股定理、等边三角形的性质、求一次函数的 解析式，关键是做出辅助线得出等边三角形． 　 五、解答题（三）（本大题共 3 小题，每小题 9 分，共 27 分） 23．（9 分）（2013•德庆县二模）已知 P（﹣3，m）和 Q（1，m）是抛物线 y=2x2+bx+1 上的两点． （1）求 b 的值； （2）判断关于 x 的一元二次方程 2x2+bx+1=0 是否有实数根，若有，求出它的实数根；若没有，请说明理 由； （3）将抛物线 y=2x2+bx+1 的图象向上平移 k（k 是正整数）个单位，使平移后的图象与 x 轴无交点，求 k 的最小值． 考点： 抛物线与 x 轴的交点；二次函数图象与几何变换． 分析： （1）根据对称轴的定义观察点 P（﹣3，m）和 Q（1，m）纵坐标相同，求出对称轴，从而求出 b 值； （2）把 b 值代入一元二次方程，根据方程的判别式来判断方程是否有根； （3）先将抛物线向上平移，在令 y=0，得到一个新方程，此方程无根，令△＜0，解出 k 的范围，从 而求出 k 的最小值． 解答： 解：（1）∵点 P、Q 在抛物线上且纵坐标相同， ∴P、Q 关于抛物线对称轴对称并且到对称轴距离相等． ∴抛物线对称轴 ， ∴b=4．（2）由（1）可知，关于 x 的一元二次方程为 2x2+4x+1=0． ∵△=b2﹣4ac=16﹣8=8＞0， ∴方程有实根， ∴x= = =﹣1± ；（3）由题意将抛物线 y=2x2+bx+1 的图象向上平移 k（k 是正 整数）个单位，使平移后的图象与 x 轴无交点， ∴设为 y=2x2+4x+1+k， ∴方程 2x2+4x+1+k=0 没根， ∴△＜0， ∴16﹣8（1+k）＜0， ∴k＞1， ∵k 是正整数， ∴k 的最小值为 2． 点评： 此题主要考查一元二次方程与函数的关系及函数平移的知识． 　 24．（9 分）（2012•济南）如图 1，在菱形 ABCD 中，AC=2，BD=2 ，AC，BD 相交于点 O． （1）求边 AB 的长； （2）如图 2，将一个足够大的直角三角板 60°角的顶点放在菱形 ABCD 的顶点 A 处，绕点 A 左右旋转， 其中三角板 60°角的两边分别与边 BC，CD 相交于点 E，F，连接 EF 与 AC 相交于点 G． ①判断△AEF 是哪一种特殊三角形，并说明理由； ②旋转过程中，当点 E 为边 BC 的四等分点时（BE＞CE），求 CG 的长． 考点： 相似三角形的判定与性质；全等三角形的判定与性质；等边三角形的判定与性质；勾股定理；菱形 的性质． 专题： 几何综合题． 分析： （1）根据菱形的性质，确定△AOB 为直角三角形，然后利用勾股定理求出边 AB 的长度； （2）①本小问为探究型问题．要点是确定一对全等三角形△ABE≌△ACF，得到 AE=AF，再根据已 知条件∠EAF=60°，可以判定△AEF 是等边三角形； ②本小问为计算型问题．要点是确定一对相似三角形△CAE∽△CFG，由对应边的比例关系求出 CG 的长度． 解答： 解：（1）∵四边形 ABCD 是菱形， ∴AC⊥BD， ∴△AOB 为直角三角形，且 OA= AC=1，OB= BD= ． 在 Rt△AOB 中，由勾股定理得： AB= = =2．（2）①△AEF 是等边三角形．理由如下： ∵由（1）知，菱形边长为 2，AC=2， ∴△ABC 与△ACD 均为等边三角形， ∴∠BAC=∠BAE+∠CAE=60°， 又∵∠EAF=∠CAF+∠CAE=60°， ∴∠BAE=∠CAF． 在△ABE 与△ACF 中， ∵ ， ∴△ABE≌△ACF（ASA）， ∴AE=AF， ∴△AEF 是等腰三角形， 又∵∠EAF=60°， ∴△AEF 是等边三角形． ②BC=2，E 为四等分点，且 BE＞CE， ∴CE= ，BE= ． 由①知△ABE≌△ACF， ∴CF=BE= ． ∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°（三角形内角和定理）， ∠AEG=∠FCG=60°（等边三角形内角）， ∠EGA=∠CGF（对顶角） ∴∠EAC=∠GFC． 在△CAE 与△CFG 中， ∵ ， ∴△CAE∽△CFG， ∴ ，即 ， 解得：CG= ． 点评： 本题是几何综合题，综合考查了相似三角形、全等三角形、四边形（菱形）、三角形（等边三角形 和等腰三角形）、勾股定理等重要知识点．虽然涉及考点众多，但本题着重考查基础知识，难度不 大，需要同学们深刻理解教材上的基础知识，并能够熟练应用． 　 25．（9 分）（2010•青岛）已知：把 Rt△ABC 和 Rt△DEF 按如图（1）摆放（点 C 与点 E 重合），点 B、 C（E）、F 在同一条直线上．∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm． 如图（2），△DEF 从图（1）的位置出发，以 1cm/s 的速度沿 CB 向△ABC 匀速移动，在△DEF 移动的同 时，点 P 从△ABC 的顶点 B 出发，以 2cm/s 的速度沿 BA 向点 A 匀速移动．当△DEF 的顶点 D 移动到 AC 边上时，△DEF 停止移动，点 P 也随之停止移动、DE 与 AC 相交于点 Q，连接 PQ，设移动时间为 t（s）（ 0＜t＜4.5）解答下列问题： （1）当 t 为何值时，点 A 在线段 PQ 的垂直平分线上？ （2）连接 PE，设四边形 APEC 的面积为 y（cm2），求 y 与 t 之间的函数关系式；是否存在某一时刻 t， 使面积 y 最小？若存在，求出 y 的最小值；若不存在，说明理由； （3）是否存在某一时刻 t，使 P、Q、F 三点在同一条直线上？若存在，求出此时 t 的值；若不存在，说明 理由． 考点： 二次函数的最值；线段垂直平分线的性质；勾股定理；相似三角形的判定与性质． 专题： 压轴题． 分析： （1）因为点 A 在线段 PQ 垂直平分线上，所以得到线段相等，可得 CE=CQ，用含 t 的式子表示出 这两个线段即可得解； （2）作 PM⊥BC，将四边形的面积表示为 S△ABC﹣S△BPE 即可求解； （3）假设存在符合条件的 t 值，由相似三角形的性质即可求得． 解答： 解：（1）∵点 A 在线段 PQ 的垂直平分线上， ∴AP=AQ； ∵∠DEF=45°，∠ACB=90°，∠DEF+∠ACB+∠EQC=180°， ∴∠EQC=45°； ∴∠DEF=∠EQC； ∴CE=CQ； 由题意知：CE=t，BP=2t， ∴CQ=t； ∴AQ=8﹣t； 在 Rt△ABC 中，由勾股定理得：AB=10cm； 则 AP=10﹣2t； ∴10﹣2t=8﹣t； 解得：t=2； 答：当 t=2s 时，点 A 在线段 PQ 的垂直平分线上；（2）过 P 作 PM⊥BE，交 BE 于 M ∴∠BMP=90°； 在 Rt△ABC 和 Rt△BPM 中， ， ∴ ； ∴PM= ； ∵BC=6cm，CE=t，∴BE=6﹣t； ∴y=S△ABC﹣S△BPE= ﹣ = ﹣ = = ； ∵ ， ∴抛物线开口向上； ∴当 t=3 时，y 最小= ； 答：当 t=3s 时，四边形 APEC 的面积最小，最小面积为 cm2．（3）假设存在某一时刻 t，使点 P、 Q、F 三点在同一条直线上； 过 P 作 PN⊥AC，交 AC 于 N ∴∠ANP=∠ACB=∠PNQ=90°； ∵∠PAN=∠BAC， ∴△PAN∽△BAC； ∴ ； ∴ ； ∴ ， ； ∵NQ=AQ﹣AN， ∴NQ=8﹣t﹣（ ）= ∵∠ACB=90°，B、C、E、F 在同一条直线上， ∴∠QCF=90°，∠QCF=∠PNQ； ∵∠FQC=∠PQN， ∴△QCF∽△QNP； ∴ ，∴ ； ∵0＜t＜4.5，∴ ； 解得：t=1； 答：当 t=1s，点 P、Q、F 三点在同一条直线上． 点评： 此题考查了相似三角形的判定与性质、二次函数的最值、特殊图形的面积的求法等知识，图形较复 杂，考查学生数形结合的能力，综合性强，难度较大．