高考数学立体几何部分知识点归纳

高考数学立体几何部分知识点归纳

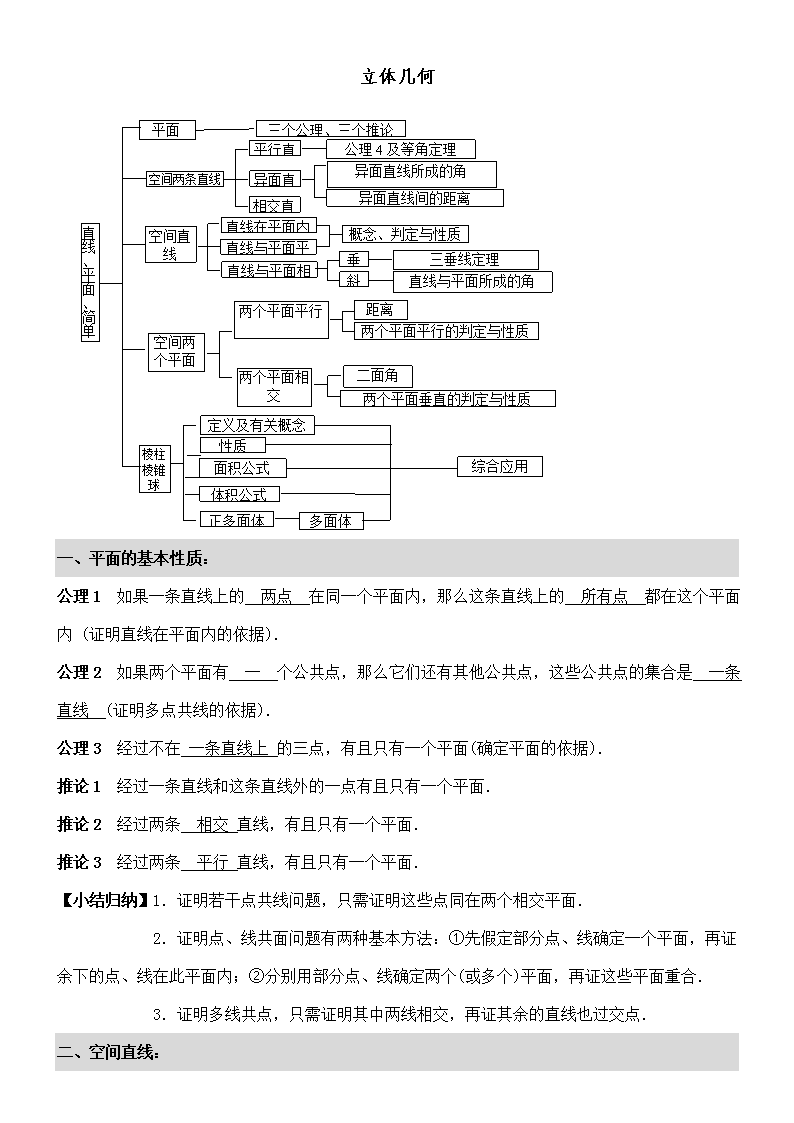
立体几何 直线、平面、简单几何体 三个公理、三个推论 平面 平行直线 异面直线 相交直线 公理4及等角定理 异面直线所成的角 异面直线间的距离 直线在平面内 直线与平面平行 直线与平面相交 空间两条直线 概念、判定与性质 三垂线定理 垂直 斜交 直线与平面所成的角 空间直线 与平面 空间两个平面 棱柱 棱锥 球 两个平面平行 两个平面相交 距离 两个平面平行的判定与性质 两个平面垂直的判定与性质 二面角 定义及有关概念 性质 综合应用 多面体 面积公式 体积公式 正多面体 一、平面的基本性质：‎ 公理1 如果一条直线上的 两点 在同一个平面内，那么这条直线上的 所有点 都在这个平面内 (证明直线在平面内的依据)． 公理2 如果两个平面有 一 个公共点，那么它们还有其他公共点，这些公共点的集合是 一条直线 (证明多点共线的依据)． 公理3 经过不在 一条直线上 的三点，有且只有一个平面(确定平面的依据)． 推论1 经过一条直线和这条直线外的一点有且只有一个平面． 推论2 经过两条 相交 直线，有且只有一个平面． 推论3 经过两条 平行 直线，有且只有一个平面．‎ ‎【小结归纳】1．证明若干点共线问题，只需证明这些点同在两个相交平面． ‎ 2．证明点、线共面问题有两种基本方法：①先假定部分点、线确定一个平面，再证余下的点、线在此平面内；②分别用部分点、线确定两个(或多个)平面，再证这些平面重合． ‎ 3．证明多线共点，只需证明其中两线相交，再证其余的直线也过交点． 二、空间直线：‎ ‎1．空间两条直线的位置关系为 平行 、 相交 、 异面 ． ‎2．相交直线 有且仅有 一个公共点，平行直线 无 没有公共点，异面直线：不同在任 一个 平面，没有公共点． ‎3．公理4：平行于同一条直线的两条直线互相 平行 ． ‎4．等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两角 相等 ． ‎5．异面直线的判定定理：过平面外一点与平面内一点的直线和平面内 不过这点 的直线是异面直线(作用：判定两条直线是异面直线) ‎6．异面直线的距离：和两条异面直线 都垂直相交 的直线称为异面直线的公垂线．两条异面直线的公垂线在 的长度，叫两异面直线的距离．‎ ‎【小结归纳】1．求两条异面直线所成角的步骤：(1)找出或作出有关角的图形；(2)证明它符合定义；(3)求角．‎ ‎ 2．证明两条直线异面的常用方法：反证法、定义法(排除相交或平行)、定理法．‎ ‎ 3．求异面直线间距离的方法：作出公垂线段，向量法．‎ 三、直线和平面平行：‎ ‎1．直线和平面的位置关系 平行 、 包含 、 相交 ．直线在平面内，有 无数个 公共点．直线和平面相交，有 一个 公共点．直线和平面平行，没有公共点．直线与平面平行、直线与平面相交称为直线在平面外．‎ ‎2．直线和平面平行的判定定理 如果平面外 一条直线 和这个平面内 一条直线 平行，那么这条直线和这个平面平行．(记忆口诀：线线平行 线面平行)‎ ‎3．直线和平面平行的性质定理 如果一条直线和一个平面 平行 ，且经过 这条直线的另一个 平面和这个平面相交，那么这条直线和交线平行．(记忆口诀：线面平行 线线平行)‎ ‎【小结归纳】1．证明直线和平面平行的方法有：(1)依定义采用反证法；(2)判定定理；(3)面面平行性质；(4)向量法．‎ ‎ 2．辅助线(面)是解、证有关线面问题的关键，要充分发挥在化空间问题为平面问题的转化作用．‎ 四、直线和平面垂直：‎ ‎1．直线和平面垂直的定义：如果一条直线和一个平面的 所有 直线垂直，那么这条直线和这个平面互相垂直．‎ ‎2．直线和平面垂直的判定定理：如果一条直线和一个平面内的 两条相交 直线都垂直，那么这条直线垂直于这个平面．‎ ‎3．直线和平面垂直性质：若a⊥，b则 ；若a⊥，b⊥则 ；若a⊥，a⊥则 ‎ 过一点和已知平面垂直的直线有且只有一条．‎ ‎4．点到平面距离 过一点作平面的垂线 的线段长度 叫做点到平面的距离．‎ ‎5．直线到平面的距离 一条直线与一个平面平行时，这条直线上 到这个平面的距离叫做直线到平面距离．‎ ‎【小结归纳】线面垂直的判定方法：(1) 线面垂直的定义；(2)判定定理；(3) 面面垂直的性质；(4) 面面平行的性质：若∥，a⊥则a ⊥。‎ 五、三垂线定理：‎ ‎1．和一个平面相交，但不和这个平面 垂直 的直线叫做平面的斜线，斜线和平面的交点叫做 交点 ．‎ ‎2．射影(1) 平面外一点向平面引垂线的 叫做点在平面内的射影；(2) 过垂足和斜足的直线叫斜线在平面内的 ．斜线上任意一点在平面上的射影一定在 ．垂线在平面上的射影只是 ．直线和平面平行时，直线在平面上的射影是和该直线 的一条直线．‎ C O B A ‎3．如图，AO是平面斜线，A为斜足，OB⊥，B为垂足，AC，∠OAB＝，BAC＝，∠OAC＝，则cos＝ ．‎ ‎4．直线和平面所成的角平面的斜线和它在这个平面内的 所成的 ‎ 叫做这条直线和平面所成角．‎ 斜线和平面所成角，是这条斜线和平面内任一条直线所成角中 ．‎ ‎5．三垂线定理：在平面内的一条直线如果和这个平面的一条斜线的 垂直，那么它也和 垂直．‎ 逆定理：在平面内的一条直线，如果和这个平面的一条 垂直，那么它也和这条 垂直．‎ ‎【小结归纳】1．求直线和平面所成的角的一般步骤是一找(作)，二证，三算．寻找直线在平面内的射影是关键，基本原理是将空间几何问题转化为平面几何问题，主要转化到一个三角形内，通过解三角形来解决．‎ ‎ 2．三垂线定理及逆定理，是判定两条线互相垂直的重要方法，利用它解题时要抓住如下几个环节：一抓住斜线，二作出垂线，三确定射影．‎ ‎ ３．证明线线垂直的重要方法：三垂线定理及逆定理；线⊥面线⊥线；向量法．‎ 六、平面和平面平行：‎ ‎1．两个平面的位置关系： ‎ ‎2．两个平面平行的判定定理：如果一个平面内有两条 直线分别平行于另一个平面，那么这两个平面平行．(记忆口诀：线面平行，则面面平行)‎ ‎3、两个平面平行的性质定理：如果两个平行平面同时与第三个平面相交，那么它所有的 平行．（记忆口诀：面面平行，则线线平行)‎ ‎4．两个平行平面距离：和两个平行平面同时 的直线，叫做两个平面的公垂线，公垂线夹在平行平面间的部分叫做两个平面的 ，两个平行面的公垂线段的 ，叫做两个平行平面的距离．‎ ‎【小结归纳】1．判定两个平面平行的方法：(1)定义法；(2)判定定理．‎ ‎ 2．正确运用两平面平行的性质．‎ ‎ 3．注意线线平行，线面平行，面面平行的相互转化：线∥线线∥面面∥面．‎ 七、两个平面垂直：‎ ‎1．两个平面垂直的定义：如果两个平面相交所成二面角为 二面角，则这两个平面互相垂直．‎ ‎2．两个平面垂直的判定：如果一个平面 有一条直线 另一个平面，则这两个平面互相垂直．‎ ‎3．两个平面垂直的性质：如果两个平面垂直，那么一个平面 的垂直于它们的 的直线垂直于另一个平面．‎ ‎4．异面直线上两点间的距离公式：EF＝，其中：d是异面直线a、b的 ，θ为a、b ，m、n分别是a、b上的点E、F到 AA'与a、b的交点A，A'的距离．‎ ‎【小结归纳】在证明两平面垂直时，一般方法是从现有的直线中寻找平面的垂线；若没有这样的直线，则可通过作辅助线来解决，而作辅助线则应有理论根据并且要有利于证明，不能随意添加，在有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后再转化为线线垂直．“线线垂直”、“线面垂直”、“面面垂直”间的转化是解决这类问题的关键。‎ 八、空间的角：‎ ‎1．两异面直线所成的角：直线a、b是异面直线，经过空间一点O分别引直线a' a，b' b，把直线a'和b'所成的 或 叫做两条异面直线a、b所成的角，其范围是 ．‎ ‎2．直线和平面所成的角：平面的一条斜线和它在平面上的 所成的 角，叫做这条斜线和平面所成的角．‎ 规定： ① 一条直线垂直于平面，我们说它们所成的角是 角；② 一条直线与平面平行或在平面内，我们说它们所成的角是 角．其范围是 ．公式：cosθ＝cosθ1cosθ2，其中，θ1是 ，θ2是 ，θ是 ．‎ ‎3．二面角：从一条直线出发的 所组成的图形叫做二面角．‎ ‎4．二面角的平面角：以二面角的棱上 一点为端点，在两个面内分别作 棱的两条射线，这两条射线所成的角叫做二面角的平面角，其范围是 ．‎ ‎【小结归纳】1．两异面直线所成角的作法：① 平移法：在异面直线中的一条直线上选择“特殊点”，作另一条直线的平行线，常常利用中位线或成比例线段引平行线；② 补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的是容易作出两条异面直线所成的角．‎ ‎ 2．作出直线和平面所成角的关键是作垂线，找射影．‎ ‎ 3．平面角的作法：① 定义法；② 三垂线法；③ 垂面法．‎ ‎ 4．二面角计算，一般是作出平面角后，通过解三角形求出其大小，也可考虑利用射影面积公式 S'＝Scosθ来求．‎ ‎ 5．空间角的计算有时也可以利用向量的求角公式完成．‎ 九、空间距离：‎ ‎1．点与点的距离：两点间 的长．‎ ‎2．点与线的距离：点到直线的 的长．‎ ‎3．平行线间的距离：从两条平行线中一条上 一点向另一条引垂线，这点到 之间的线段长．‎ ‎4．点与面的距离：点到平面的 的长．‎ ‎5．平行于平面的直线与平面的距离：直线上 一点到平面的 的长．‎ ‎6．两个平行平面间的距离：从其中一个平面上 一点向另一个平面引垂线，这点到 之间的线段长．‎ ‎7．两条异面直线的距离：与两条异面直线都 的直线夹在两 间线段的长．‎ ‎【小结归纳】1．对于空间距离的重点是点到直线、点到平面的距离，对于两异面直线的距离一般只要求会求给出公垂线段时的距离．‎ ‎ 2、求点到平面的距离的方法：‎ ‎ ⑴ 确定点在平面射影的位置，要注意利用面面垂直求作线面垂直及某些特殊性质．‎ ‎ ⑵ 转化法．即化归为相关点到平面的距离或转化为线面距或转化为面面距来求.‎ ‎ (3) 等体积法：利用三棱锥的体积公式，建立体积相等关系求出某底上的高，即点面距.‎ ‎ 3．距离问题有时也可以利用向量的模的计算解决．具体见第11节的小结4、5两点.‎ 十、棱锥、棱柱：‎ ‎（一）棱柱 ‎1．定义：如果一个多面体有两个面互相 ，而其余每相邻两个面的交线互相 ，这样的多面体叫做棱柱，两个互相平行的面叫做棱柱的 ，其余各面叫做棱柱的 ，两侧面的公共边叫做棱柱的 ，两个底面所在平面的公垂线段，叫做棱柱的 ．‎ ‎2．性质：① 侧棱 ，侧面是 ；② 两个底面与平行于底面的截面是对应边互相平行的 多边形；③ 过不相邻的两条侧棱的截面是 四边形．‎ ‎3．分类：① 按底面边数可分为 ；② 按侧棱与底面是否垂直可分为：‎ 棱柱 ‎ ‎4．特殊的四棱柱：四棱柱→平行六面体→直平行六面体→长方体→正四棱柱→正方体．‎ ‎5．长方体对角线的性质：长方体一条对角线的平方等于一个顶点上三条棱长的 ．‎ ‎（二）棱锥 ‎1．定义：如果一个多面体的一个面是 ，其余各面是有一个公共顶点的 ，那么这个多面体叫做棱锥，有公共顶点的各三角形，叫做棱锥的 ；余下的那个多边形，叫做棱锥的 ．两个相邻侧面的公共边，叫做棱锥的 ，各侧面的公共顶点，叫做棱锥的 ；由顶点到底面所在平面的垂线段，叫做棱锥的 ．‎ ‎2．性质：如果棱锥被平行于底面的平面所截，那么所得的截面与底面 ，截面面积与底面面积的比等于顶点到截面距离与棱锥高的 ．‎ ‎3．正棱锥的定义：如果一个棱锥的底面是 多边形，且顶点在底面的射影是底面的 ，这样的棱锥叫做正棱锥．‎ ‎4．正棱锥的性质：‎ ‎① 正棱锥各侧棱 ，各侧面都是 的等腰三角形，各等腰三角形底边上的高 （它叫做正棱锥的 ）；‎ ‎② 正棱锥的高、斜高和斜高在底面内的射影组成一个 三角形，正棱锥的高、侧棱、侧棱在底面内的射影组成一个 三角形．‎ ‎【小结归纳】柱体和锥体是高考立体几何命题的重要载体，因此，在学习时要注意以下三点．‎ ‎1．要准确理解棱柱、棱锥的有关概念，弄清楚直棱柱、正棱锥概念的内涵和外延．‎ ‎2．要从底面、侧面、棱(特别是侧棱)和截面(对角面及平行于底面的截面)四个方面掌握几何性质，能应用这些性质研究线面关系．‎ ‎3．在解正棱锥问题时，要注意利用四个直角三角形，其中分别含有九个元素(侧棱、高、侧棱与斜高在底面上的射影、侧棱与侧面与底面所成角、边心距以及底面边的一半)中的三个，已知两个可求另一个．‎ 十一、球：‎ ‎1．球：与定点的距离 或 定长的点的集合．‎ ‎2．球的性质 ‎(1) 用一个平面去截一个球，截面是 ．‎ ‎(2)球心和截面圆心的连线 于截面．‎ ‎(3) 球心到截面的距离与球半径及截面的半径有以下关系： ．‎ ‎(4) 球面被经过球心的平面截得的圆叫 ．被不经过球心的平面截得的圆叫 ．‎ ‎(5) 在球面上两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧长，这个弧长叫 ．‎ ‎3．球的表面积公式和体积公式：设球的半径为R，则球的表面积S＝ ；球的体积V＝ ．‎ ‎【小结归纳】1．因为“球”是“圆”在空间概念上的延伸，所以研究球的性质时，应注意与圆的性质类比．‎ ‎2．球的轴截面是大圆，它含有球的全部元素，所以有关球的计算，可作出球的一个大圆，化“球”为“圆”来解决问题．‎ ‎3．球心与小圆圆心的连线，垂直于小圆所在的平面，球的内部结构的计算也由此展开．‎ ‎4．计算球面上A、B两点的球面距离是一个难点，其关键是利用“AB既是小圆的弦，又是大圆的弦”这一事实，其一般步骤是：‎ ‎(1) 根据已知条件求出小圆的半径r和大圆的半径R，以及所对小圆圆心角；‎ ‎(2) 在小圆中，由r和圆心角求出AB；‎ ‎(3) 在大圆中，由AB和R求出大圆的圆心角；‎ ‎(4) 由圆心角和R，求出大圆弧长AB (即球面上A、B两点的距离)．‎