高中数学 概率单元测试

高中数学 概率单元测试

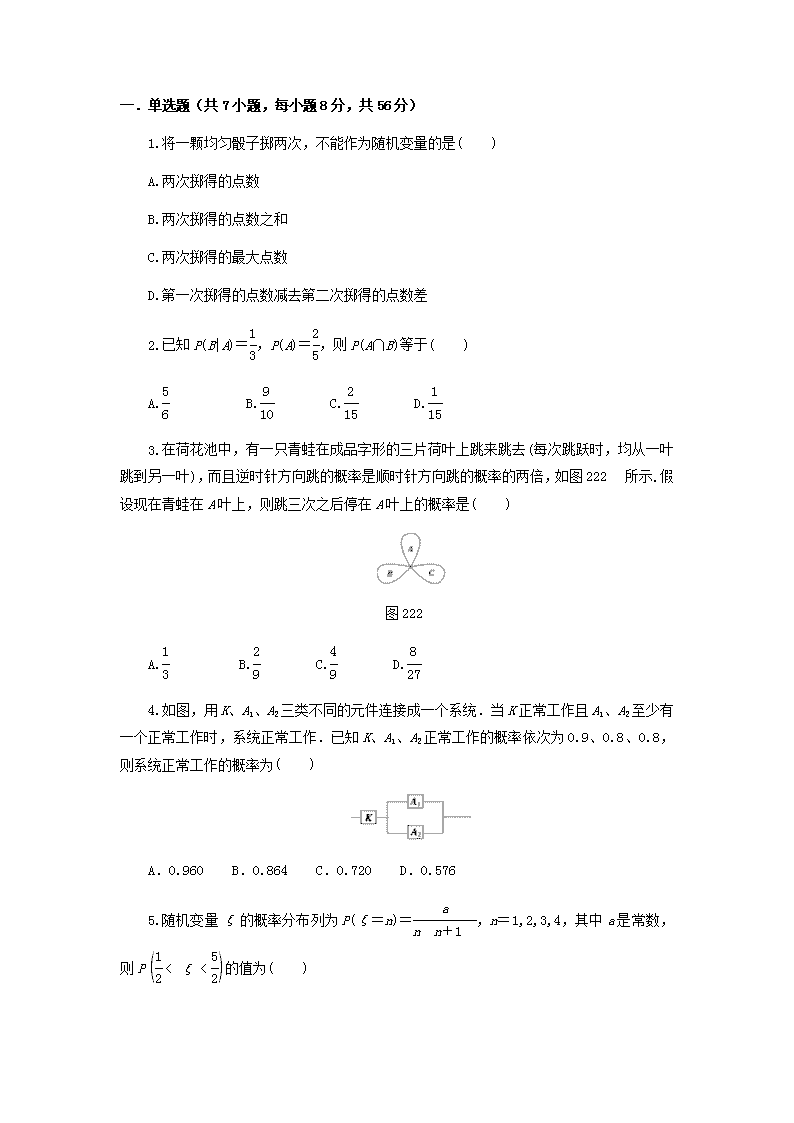
一．单选题（共7小题，每小题8分，共56分）‎ ‎1.将一颗均匀骰子掷两次，不能作为随机变量的是(　　)‎ A.两次掷得的点数 B.两次掷得的点数之和 C.两次掷得的最大点数 D.第一次掷得的点数减去第二次掷得的点数差 ‎2.已知P(B|A)＝，P(A)＝，则P(A∩B)等于(　　)‎ A.　　　 B. C. D. ‎3.在荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时，均从一叶跳到另一叶)，而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图222所示.假设现在青蛙在A叶上，则跳三次之后停在A叶上的概率是(　　)‎ 图222‎ A. B. C. D. ‎4.如图，用K、A1、A2三类不同的元件连接成一个系统．当K正常工作且A1、A2至少有一个正常工作时，系统正常工作．已知K、A1、A2正常工作的概率依次为0.9、0.8、0.8，则系统正常工作的概率为(　　)‎ A．0.960 B．0.864 C．0.720 D．0.576‎ ‎5.随机变量ξ的概率分布列为P(ξ＝n)＝，n＝1,2,3,4，其中a是常数，则P的值为(　　)‎ A. B. C. D. ‎6.掷一枚质地均匀的骰子n次，设出现k次点数为1的概率为Pn(k)，若n＝20，则当Pn(k)取最大值时，k为(　　)‎ A.3 B.4 ‎ C.8 D.10‎ ‎7. 已知随机变量ξ服从正态分布N(2，σ2)，且P(ξ<4)＝0.8，则P(0<ξ<2)＝(　　)‎ A.0.6 B.0.4‎ C.0.3 D.0.2‎ 二．多选题（共2小题，每小题8分，共16分）‎ ‎8．下列说法正确的是(　　)‎ A.某辆汽车一年中发生事故的次数是一个离散型随机变量 B.正态分布随机变量等于一个特定实数的概率为0‎ C.公式E(X)＝np可以用来计算离散型随机变量的均值 D.从一副扑克牌中随机抽取5张，其中梅花的张数服从超几何分布 ‎9.已知甲盒中仅有1个球且为红球，乙盒中有个红球和个篮球，从乙盒中随机抽取个球放入甲盒中.‎ ‎（a）放入个球后，甲盒中含有红球的个数记为；‎ ‎（b）放入个球后，从甲盒中取1个球是红球的概率记为.则下列选项正确的是（ ）‎ A. B. ‎ C. D. ‎ 三．填空题（共2小题，每小题8分，共16分）‎ ‎10.已知随机变量X只能取三个值x1，x2，x3，其概率依次成等差数列，则公差d 的取值范围为________.‎ ‎11.设离散型随机变量X可能的取值为1,2,3，P(X＝k)＝ak＋b(k＝1,2,3).又X的均值E(X)＝3，则a＋b＝________. ‎ 四．解答题（共1小题，第1问6分，第2问6分，共12分）‎ ‎12. 某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为．现安排甲组研发新产品，乙组研发新产品．设甲、乙两组的研发相互独立．‎ ‎(1)求至少有一种新产品研发成功的概率；‎ ‎(2)若新产品研发成功，预计企业可获利润120万元；若新产品研发成功，预计企业可获利润100万元．求该企业可获利润的分布列和数学期望．‎ 一．单选题（共7小题）‎ ‎1..将一颗均匀骰子掷两次，不能作为随机变量的是(　　)‎ A.两次掷得的点数 B.两次掷得的点数之和 C.两次掷得的最大点数 D.第一次掷得的点数减去第二次掷得的点数差 ‎【解析】　两次掷得的点数的取值是一个数对，不是一个数.‎ ‎【答案】　A ‎2.已知P(B|A)＝，P(A)＝，则P(A∩B)等于(　　)‎ A.　　　　 B. C. D. ‎【解析】　由P(B|A)＝，得P(A∩B)＝P(B|A)·P(A)＝×＝.‎ ‎【答案】　C ‎3.在荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时，均从一叶跳到另一叶)，而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图222所示.假设现在青蛙在A叶上，则跳三次之后停在A叶上的概率是(　　)‎ 图222‎ A. B. ‎ C. D. ‎【解析】　青蛙跳三次要回到A只有两条途径：‎ 第一条：按A→B→C→A，‎ P1＝××＝；‎ 第二条，按A→C→B→A，‎ P2＝××＝.‎ 所以跳三次之后停在A叶上的概率为 P＝P1＋P2＝＋＝.‎ ‎【答案】　A ‎4. 如图，用K、A1、A2三类不同的元件连接成一个系统．当K正常工作且A1、A2至少有一个正常工作时，系统正常工作．已知K、A1、A2正常工作的概率依次为0.9、0.8、0.8，则系统正常工作的概率为(　　)‎ A．0.960 B．0.864 C．0.720 D．0.576‎ ‎【解析】　[方法一　由题意知K，A1，A2正常工作的概率分别为P(K)＝0.9，P(A1)＝0.8，P(A2)＝0.8.‎ ‎∵K，A1，A2相互独立，∴A1，A2至少有一个正常工作的概率为P(1A2)＋P(A12)＋P(A1A2)＝(1－0.8)×0.8＋0.8×(1－0.8)＋0.8×0.8＝0.96.∴系统正常工作的概率为P(K)[P(1A2)＋P(A12)＋P(A1A2)]＝0.9×0.96＝0.864.‎ 方法二　A1，A2至少有一个正常工作的概率为1－P(12)＝1－(1－0.8)(1－0.8)＝0.96.∴系统正常工作的概率为P(K)[1－P(12)]＝0.9×0.96＝0.864.]‎ ‎【答案】　B ‎5.随机变量ξ的概率分布列为P(ξ＝n)＝，n＝1,2,3,4，其中a是常数，则P的值为(　　)‎ A. B. C. D. ‎【解析】　＋＋＋＝‎ a ‎＝a＝1.‎ ‎∴a＝.‎ ‎∴P＝P(ξ＝1)＋P(ξ＝2)‎ ‎＝×＝.‎ ‎【答案】　D ‎6.掷一枚质地均匀的骰子n次，设出现k次点数为1的概率为Pn(k)，若n＝20，则当Pn(k)取最大值时，k为(　　)‎ A.3 B.4 ‎ C.8 D.10‎ ‎【解析】　掷一枚质地均匀的骰子20次，其中出现点数为1的次数为X，X～B，Pn(k)＝C·20－k·k.‎ ＝.‎ 当1≤k≤3时，>1，Pn(k)>Pn(k－1).当k≥4时，<1，Pn(k)

查看更多