中考数学一轮复习知识点+题型专题讲义18 全等形与全等三角形（教师版）

中考数学一轮复习知识点+题型专题讲义18 全等形与全等三角形（教师版）

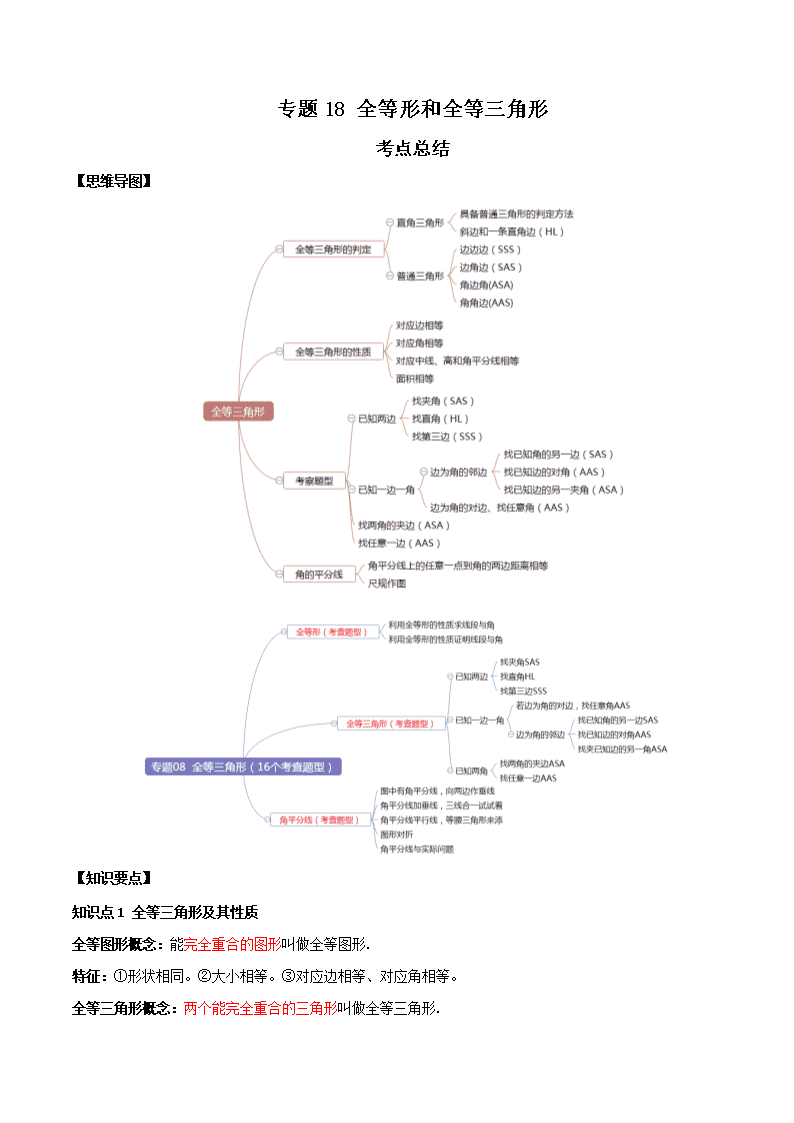
专题 18 全等形和全等三角形 考点总结 【思维导图】 【知识要点】 知识点 1 全等三角形及其性质 全等图形概念：能完全重合的图形叫做全等图形. 特征：①形状相同。②大小相等。③对应边相等、对应角相等。 全等三角形概念：两个能完全重合的三角形叫做全等三角形. 小结：把两个全等三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对 应角. 表示方法：全等用符号“≌”，读作“全等于”。书写三角形全等时，要注意对应顶点字母要写在对应位置 上。 全等变换定义：只改变图形的位置，而不改变图形的形状和大小的变换。 变换方式（常见）：平移、翻折、旋转。 全等三角形的性质：对应边相等，对应角相等。 1．（2017·四川中考模拟）已知四边形 ABCD 各边长如图所示，且四边形 OPEF≌四边形 ABCD．则 PE 的 长为（ ） A．3 B．5 C．6 D．10 【答案】D 【详解】 ∵四边形 OPEF≌四边形 ABCD ∴PE=BC=10， 故选 D. 2．（2019·福建中考模拟）如图，若△ 헀Ÿ ≌ △ th ，则点 h 应是图中的（ ） A．点 B．点 C．点 D．点 【答案】D 【详解】 ∵△MNP≌△MEQ， ∴点 Q 应是图中的 D 点，如图， 故选：D． 3．（2018·广西中考模拟）下列说法中不正确的是（ ） A．全等三角形的周长相等 B．全等三角形的面积相等 C．全等三角形能重合 D．全等三角形一定是等边三角形 【答案】D 【详解】 根据全等三角形的性质可知 A，B，C 命题均正确，故选项均错误； D.错误，全等三角也可能是直角三角，故选项正确. 故选 D. 考查题型一 利用全等三角形性质求线段与角 1．（2019·武冈市第七中学中考模拟）如图，三角形纸片 ABC，AB＝10cm，BC＝7cm，AC＝6cm，沿过点 B 的直线折叠这个三角形，使顶点 C 落在 AB 边上的点 E 处，折痕为 BD，则△AED 的周长为（ ） A．9cm B．13cm C．16cm D．10cm 【答案】A 【解析】 解：由折叠的性质知，CD=DE，BC=BE=7cm． ∵AB=10cm，BC=7cm，∴AE=AB﹣BE=3cm． △AED 的周长=AD+DE+AE=AC+AE=6+3=9（cm）． 故选 A． 2．（2017·江苏南京溧水孔镇中学中考模拟）如图，△ABC≌△DEF，点 A 与 D，B 与 E 分别是对应顶点， 且测得 BC=5cm，BF=7cm，则 EC 长为（ ） A．1cm B．2cm C．3cm D．4cm 【答案】C 【详解】 解：∵△ABC≌△BAD， ∴EF=BC=5cm， ∵BF=7cm，BC=5cm， ∴CF=EF-CF=3 cm， 故选 C． 3．（2016·广东中考模拟）如图，△ACB≌△ ,∠ACA′=30°，则∠BCB′的度数为( ) A．20° B．30° C．35° D．40° 【答案】B 【详解】 ∵△ACB≌△A′CB′， ∴∠ACB=∠A′C′B′， ∴∠ACB-∠A′CB=∠A′C′B′-∠A′CB， 即∠BCB′=∠ACA′， 又∠ACA′=30°， ∴∠BCB′=30°， 故选：B． 4．（2019·沂源县中庄中学初一月考）如图，点 B，C，D 在同一条直线上，∠B=∠D=90°，△ABC≌△ CDE,AB=6,BC=8,CE=10. （1）求△ABC 的周长； （2）求△ACE 的面积. 【答案】（1）24；（2）50 【详解】 解：（1））∵△ABC≌△CDE ∴AC=CE ∴△ABC 的周长=AB+BC+AC=24 （2）∵△ABC≌△CDE ∴AC=CE，∠ACB=∠CED，∠BAC=∠DCE 又∠B=90° ∴∠ACB+∠BAC=90° ∴∠ACB+∠DCE=90° ∴∠ACE=180°-（∠ACB+∠DCE）=90° ∴△ACE 的面积= t ൌ考查题型二 利用全等三角形性质证明线段、角相等 1．（2019·湖北黄石十四中初二期中）如图，点 E 在 AB 上，△ABC≌△DEC，求证：CE 平分∠BED． 【答案】见解析 【详解】 ∵△ABC≌△DEC， ∴∠B=∠DEC，BC=EC， ∴∠B=∠BEC， ∴∠BEC=∠DEC， ∴CE 平分∠BED． 2．（2018·颍上县第五中学初二期中）若△ABC≌△DCB，求证：∠ABE=∠DCE. 【答案】见解析 【详解】 证明：∵△ABC≌△DCB ∴∠ABC=∠DCB，∠ACB=∠DBC ∴∠ABC-∠DBC=∠DCB-∠ACB 即∠ABE=∠DCE 知识点 2：全等三角形的判定（重点） 一般三角形 直角三角形 判定 边角边（SAS）、角边角（ASA） 角角边（AAS）、边边边（SSS） 具备一般三角形的判定方法 斜边和一条直角边对应相等（HL） 性质 对应边相等，对应角相等 对应中线相等，对应高相等，对应角平分线相等 注：① 判定两个三角形全等必须有一组边对应相等； ② 全等三角形周长、面积相等． 证题的思路（重点）： 考查题型三 已知一边一角（若边为角的对边，找任意角 AAS） 1．（2018·四川中考模拟）如图，AB=AE，∠1=∠2，∠C=∠D．求证:AC=AD． 【答案】见解析 【解析】 详解：∵∠1=∠2 ∴∠1+∠EAC=∠2+∠EAC ∴∠BAC=∠EAD 在ΔABC 和ΔAED 中 ∠ ∠ t∠ ∠ t∴ΔABC≌ΔAED（AAS) ∴AC=AD 2．（2014·北京中考模拟）已知：如图，E 是 AC 上一点，AB=CE，AB∥CD，∠ACB =∠D．求证：BC =ED． 【答案】证明见解析. 【详解】 ∵AB∥CD，∴∠A=∠ECD. 在△ABC 和△ECD 中，∵∠A＝∠ECD，∠ACB＝∠D，AB＝CE， ∴△ABC≌△ECD（AAS）. ∴BC=DE． 3．（2018·四川中考模拟）已知，如图，E、F 分别为□ABCD 的边 BC、AD 上的点，且∠1=∠2,.求证：AE=CF. 【答案】详见解析 【详解】 ∵四边形 ABCD 为平行四边形 ∴∠B=∠D，AB=CD 在△ABE 与△CDF 中，∠1=∠2，∠B=∠D，AB=CD ∴△ABE≌△CDF ∴AE=CF 4．（2016·福建中考模拟）如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE．求证：△ACD≌△CBE． 【答案】证明详见解析. 【详解】 ∵AD⊥CE，BE⊥CE， ∴∠ADC=∠E=90°， ∵∠ACB=90°， ∴∠BCE+∠ACD=90°， ∵∠B+∠BCE=90°， ∴∠B=∠ACD， 在△BEC 和△CDA 中， ∠ADC=∠E=90°，∠B=∠ACD，AC=BC， ∴△ACD≌△CBE（AAS）． 考查题型四 已知一边一角（边为角的邻边（找已知角的另一边 SAS）） 1．（2016·四川中考真题）如图，C 是线段 AB 的中点，CD=BE，CD∥BE．求证：∠D=∠E． 【答案】见解析 【详解】 ∵C 是线段 AB 的中点， ∴AC=CB， ∵CD∥BE， ∴∠ACD=∠B， 在△ACD 和△CBE 中， ∵AC=CB，∠ACD=∠B，CD=BE， ∴△ACD≌△CBE（SAS）， ∴∠D=∠E． 2．（2018·云南中考模拟）如图，点 E，F 在 AB 上，AD＝BC，∠A＝∠B，AE＝BF．求证：∠C＝∠D． 【答案】证明见解析 【详解】 证明：∵AE＝BF， ∴AE+EF＝BF+EF， ∴AF＝BE， 在△ADF 与△BCE 中， AD BC A B AF BE       ∴△ADF≌△BCE（SAS）， ∴∠C＝∠D． 3．（2019·辽宁中考真题）如图，点 t ， 在 上， t ， ， ，求证： t ． 【答案】见解析； 【详解】 证明：∵ t ， ∴ t t t ，即 t ， 在 和 t 中， ∠ ∠ t ， ∴ ≌ t (SAS) ∴ t ． 考查题型五 已知一边一角（边为角的邻边（找已知边的对角 AAS）） 1．（2013·浙江中考真题）如图，△ABC 与△DCB 中，AC 与 BD 交于点 E，且∠A=∠D，AB=DC． （1）求证：△ABE≌DCE； （2）当∠AEB=50°，求∠EBC 的度数。 【答案】见解析（2）∠EBC=25° 【详解】 解（1）证明：∵在△ABE 和△DCE 中， ∠ ∠ ∠ AEB ∠ DEC AB DC ， ∴△ABE≌△DCE（AAS） （2）∵△ABE≌△DCE，∴BE=EC， ∴∠EBC=∠ECB， ∵∠EBC+∠ECB=∠AEB=50°， ∴∠EBC=25° 2．（2016·广西中考模拟）如图，已知四边形 ABCD 是平行四边形，DE⊥AB，DF⊥BC，垂足分别是 E、F， 并且 DE=DF．求证： （1）△ADE≌△CDF； （2）四边形 ABCD 是菱形． 【答案】见解析 【解析】证明：（1）∵DE⊥AB，DF⊥BC，∴∠AED=∠CFD=900。 ∵四边形 ABCD 是平行四边形，∴∠A=∠C。 在△AED 和△CFD 中： ∵ ∠ AED ∠ CFD∠ ∠ DE DF ， ∴△AED≌△CFD（AAS）。 （2）∵△AED≌△CFD，∴AD=CD。 ∵四边形 ABCD 是平行四边形，∴四边形 ABCD 是菱形。 3．（2019·陕西中考模拟）如图，四边形 ABCD 是平行四边形，BE、DF 分别是∠ABC、∠ADC 的平分线， 且与对角线 AC 分别相交于点 E、F．求证：AE=CF． 【答案】见解析. 【详解】 证明：∵平行四边形 ABCD 中，AD∥BC，AD=BC， ∴∠ACB=∠CAD． ∵BE、DF 分别是∠ABC、∠ADC 的平分线， ∴∠BEC=∠ABE+∠BAE=∠FDC+∠FCD=∠DFA， 在△BEC 与△DFA 中， ∵ ∠ t ＝∠ ∠ ＝∠ ＝ ∴△BEC≌△DFA（AAS）， ∴AF=CE， ∴AE=CF． 考查题型六 已知一边一角（边为角的邻边（找已知边的另一角 ASA）） 1．（2016·湖北中考真题）杨阳同学沿一段笔直的人行道行走,在由 A 步行到达 B 处的过程中,通过隔离带的 空隙 O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD 相交于 O,OD⊥CD,垂足为 D,已知 AB=20 米,请根据 上述信息求标语 CD 的长度. 【答案】20 米. 【解析】 试题解析：∵AB∥CD，∴∠ABO=∠CDO， ∵OD⊥CD，∴∠CDO=90°， ∴∠ABO=90°，即 OB⊥AB， ∵相邻两平行线间的距离相等， ∴OD=OB， 在△ABO 与△CDO 中， ， ∴△ABO≌△CDO（ASA）， ∴CD=AB=20（m） 2．（2015·北京中考模拟）如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E； 求证：BC=DC． 【答案】见解析 【详解】 证明：∵∠BCE=∠DCA， ∴∠BCE+∠ACE=∠DCA+∠ACE，即∠ACB=∠ECD. 在△ABC 和△EDC 中， ∵ ∠ ACB ∠ ECD AC EC ∠ ∠ t ， ∴△ABC≌△EDC（ASA）. ∴BC=DC 3．（2016·湖北中考模拟）如图，已知 EF∥MN，EG∥HN，且 FH=MG，求证：△EFG≌△NMH． 【答案】证明见解析 【解析】 ∵EF∥MN, EG∥HN, ∴∠F=∠M, ∠EGF=∠NHM. ∵FH=MG， ∴FG=MH. 在△EFG 和△NMH 中 ∵∠F=∠M, FG=MH ∠EGF=∠NHM， ∴△EFG≌△NMH（ASA） 考查题型七 已知两角，找两角的夹边 ASA 1．（2010·河北中考真题）如图，在△ABC 和△ADE 中，点 E 在 BC 边上，∠BAC＝∠DAE，∠B＝∠D， AB ＝AD, （1）试说明△ABC≌△ADE； （2）如果∠AEC＝75°，将△ADE 绕点 A 旋转一个锐角后与△ABC 重合，求这个旋转角的大小． 【答案】（1）、证明过程见解析；（2）、30° 【详解】 （1）∵∠BAC=∠DAE，AB=AD，∠B=∠D， ∴△ABC≌△ADE. （2）∵△ABC≌△ADE ∴AC=AE， ∴∠C=∠AEC=75°， ∴∠CAE=180°−∠C−∠AEC=30°， ∴△ADE 绕着点 A 逆时针旋转 30°后与△ABC 重合， ∴这个旋转角为 30°. 2．（2019·河北中考模拟）某风景区改建中，需测量湖两岸游船码头 A、B 间的距离，于是工作人员在岸边 A、B 的垂线 AF 上取两点 E、D，使 ED＝AE．再过 D 点作出 AF 的垂线 OD，并在 OD 上找一点 C，使 B、 E、C 在同一直线上，这时测得 CD 长就是 AB 的距离．请说明理由． 【答案】证明见解析. 【详解】 证明：∵AB⊥AD，CD⊥AD， ∴∠A＝∠CDE＝90°， 又∵ED＝AE，∠AEB＝∠CED， ∴△ABE≌△CED(AAS)， ∴AB＝CD． 3．（2018·湖北中考模拟）如图，BD⊥AC 于点 D，CE⊥AB 于点 E，AD=AE．求证：BE=CD． 【答案】证明过程见解析 【详解】 ∵BD⊥AC 于点 D，CE⊥AB 于点 E， ∴∠ADB=∠AEC=90°， 在△ADB 和△AEC 中， ∠ ∠ t t ∠ ∠ ∴△ADB≌△AEC（ASA） ∴AB=AC， 又∵AD=AE， ∴BE=CD． 考查题型八 已知两角，找任意一边 AAS 1．（2017·湖北中考模拟）如图，点 E，F 在 BC 上，BE＝CF，∠A＝∠D，∠B＝∠C，AF 与 DE 交于点 O． (1)求证：AB＝DC； (2)试判断△OEF 的形状，并说明理由． 【答案】（1）证明略 （2）等腰三角形，理由略 【详解】 证明：（1）∵BE＝CF， ∴BE＋EF＝CF＋EF， 即 BF＝CE． 又∵∠A＝∠D，∠B＝∠C， ∴△ABF≌△DCE（AAS）， ∴AB＝DC． （2）△OEF 为等腰三角形 理由如下：∵△ABF≌△DCE， ∴∠AFB=∠DEC． ∴OE=OF． ∴△OEF 为等腰三角形． 2．（2019·山西中考真题）已知：如图，点 B，D 在线段 AE 上，AD=BE，AC∥EF，∠C=∠H.求证：BC=DH. 【答案】证明见解析. 【详解】 ∵AD=BE， ∴AD-BD=BE-BD， 即 AB=DE. ∵AC∥EH， ∴∠A=∠E， 在△ABC 和△EDH 中 ∠ ∠ ∠ ∠ t t ， ∴△ABC≌△EDH(AAS)， ∴BC=DH. 3．（2019·广西中考模拟）已知：如图，点 B、F、C、E 在同一条直线上，AB∥DE，∠A＝∠D，BF＝EC． （1）求证：△ABC≌△DEF． （2）若∠A＝120°，∠B＝20°，求∠DFC 的度数． 【答案】（1）见解析；（2）∠DFC＝40° 【详解】 （1）证明：∵AB∥DE， ∴∠B＝∠E， ∵BF＝EC ∴BF+FC＝EC+CF， 即 BC＝EF， 在△ABC 和△DEF 中， ∠ ∠ ∠ ∠ t t ， ∴△ABC≌△DEF（AAS）； （2）解：∵∠A＝120°，∠B＝20°， ∴∠ACB＝40°， 由（1）知△ABC≌△DEF， ∴∠ACB＝∠DFE， ∴∠DFE＝40°， ∴∠DFC＝40°． 4．（2016·江苏中考模拟）如图，在四边形 ABCD 中，AD∥BC，∠A=90°，CE⊥BD 于 E，AB=EC． （1）求证：△ABD≌△ECB； （2）若∠EDC=65°，求∠ECB 的度数； （3）若 AD=3，AB=4，求 DC 的长． 【答案】（1）证明见解析；（2）40°；（3）2 ൌ ． 【解析】 （1）证明：∵AD∥BC， ∴∠ADB=∠EBC， ∵∠A=∠CEB=90°， 在△ABD 与△CEB 中， ∠ ∠ t∠ ∠ t t ， ∴△ABD≌△ECB； （2）由（1）证得△ABD≌△ECB， ∴BD=BC， ∴∠BCD=∠BDC=65°， ∵∠DCE=90°-65°=25°， ∴∠ECB=40°； （3）由（1）证得△ABD≌△ECB， ∴CE=AB=4，BE=AB=3， ∴BD=BC= ൌ ， ∴DE=2， ∴CD= ൌ ． 考查题型九 已知两边，找夹角 SAS 1．（2013·湖北中考真题）如图，点 D，E 在△ABC 的边 BC 上，AB=AC，BD=CE．求证：AD=AE． 【解析】 证明：∵AB=AC，∴∠B=∠C。 在△ABD 与△ACE 中，∵ AB AC ∠ ∠ BD EC ， ∴△ABD≌△ACE（SAS）。 ∴AD=AE。 2．（2018·广东中考真题）如图，AB 与 CD 相交于点 E，AE＝CE，DE＝BE．求证：∠A＝∠C． 【答案】证明见解析． 【详解】 在△AED 和△CEB 中， t t ∠ t ∠ t t t ， ∴△AED≌△CEB（SAS）， ∴∠A＝∠C（全等三角形对应角相等）． 3．（2019·江苏中考真题）如图，在△ABC 中，AB=AC,点 D、E 分别在 AB、AC 上，BD=CE，BE、CD 相 交于点 0； 求证：（1） ≅ t （2） 【答案】（1）见解析；（2）见解析. 【详解】 (1)∵AB=AC， ∴∠ECB=∠DBC， 在 与 t 中 t ∠ ∠ t ， ∴ ≅ t ； (2)由(1) ≅ t ， ∴∠DCB=∠EBC， ∴OB=OC. 4．（2018·江苏中考模拟）如图，在五边形 ABCDE 中，∠BCD=∠EDC=90°，BC=ED，AC=AD． （1）求证：△ABC≌△AED； （2）当∠B=140°时，求∠BAE 的度数． 【答案】（1）详见解析；（2）80°． 【详解】 证明：（1）∵AC=AD， ∴∠ACD=∠ADC， 又∵∠BCD=∠EDC=90°， ∴∠ACB=∠ADE， 在△ABC 和△AED 中， t ∠ ∠ t ， ∴△ABC≌△AED（SAS）； 解：（2）当∠B=140°时，∠E=140°， 又∵∠BCD=∠EDC=90°， ∴五边形 ABCDE 中，∠BAE=540°﹣140°×2﹣90°×2=80°． 5．（2019·河北中考模拟）如图，△BAD 是由△BEC 在平面内绕点 B 旋转 60°而得，且 AB⊥BC，BE＝CE， 连接 DE． （1）求证：△BDE≌△BCE； （2）试判断四边形 ABED 的形状，并说明理由． 【答案】证明见解析. 【详解】 （1）证明：∵△BAD 是由△BEC 在平面内绕点 B 旋转 60°而得， ∴DB=CB，∠ABD=∠EBC，∠ABE=60°， ∵AB⊥EC， ∴∠ABC=90°， ∴∠DBE=∠CBE=30°， 在△BDE 和△BCE 中， ∵ DB CB ∠ DBE ∠ CBE BE BE ， ∴△BDE≌△BCE； （2）四边形 ABED 为菱形； 由（1）得△BDE≌△BCE， ∵△BAD 是由△BEC 旋转而得， ∴△BAD≌△BEC， ∴BA=BE，AD=EC=ED， 又∵BE=CE， ∴BA=BE=ED= AD ∴四边形 ABED 为菱形． 考查题型十已知两边，找直角 HL 1．（2018·江苏中考真题）如图，∠A=∠D=90°，AC=DB，AC、DB 相交于点 O．求证：OB=OC． 【答案】证明见解析. 【解答】证明：在 Rt△ABC 和 Rt△DCB 中 ， ∴Rt△ABC≌Rt△DCB（HL）， ∴∠OBC=∠OCB， ∴BO=CO． 2．（2019·江苏中考模拟）如图所示，在△ABC 中，D 是 BC 的中点，DE⊥AB，DF⊥AC，垂足分别是点 E， F，且 BE=CF，求证：AD 是△ABC 的角平分线． 【答案】见解析 【详解】 证明：∵DE⊥AB，DF⊥AC， ∴△BDE△DCF 是直角三角形． 在 Rt△BDE 与 Rt△DCF 中， t ， ∴Rt△BDE≌Rt△DCF（HL）， ∴DE=DF， 又∵DE⊥AB，DF⊥AC， ∴AD 是△ABC 的角平分线． 3．（2019·福建省诏安县霞葛初级中学中考模拟）如图， 、 、 、 四点在一条直线上，AB DE ， ， t ，垂足分别为点 、点 ， ． 求证： （1） ≅ t ； （2） 䁡䁡t ． 【答案】（1）见解析；（2）见解析. 【详解】 证明： （1）∵ ， t ⊥ ， ∴ 和 t 为直角三角形， ∵ ， ∴ ，即 ， 在 和 t 中， t ， ∴ ≅ t ； （2）由（1）可知 ≅ t ， ∴∠ ∠ ， ∴ 䁡䁡t ． 考查题型十一 已知两边，找第三边 SSS 1．（2018·四川中考模拟）如图，点 B、E、C、F 在同一条直线上，AB＝DE，AC＝DF，BE＝CF，求证： AB∥DE． 【答案】详见解析. 【解析】 证明：由 BE＝CF 可得 BC＝EF， 又 AB＝DE，AC＝DF， 故△ABC≌△DEF（SSS）， 则∠B=∠DEF， ∴AB∥DE． 2．（2018·广西中考真题）如图，点 A、D、C、F 在同一条直线上，AD=CF，AB=DE，BC=EF. (1)求证：ΔABC≌△DEF； (2)若∠A=55°，∠B=88°，求∠F 的度数. 【答案】（1）证明见解析；（2）37° 【解析】 （1）∵AC=AD+DC， DF=DC+CF，且 AD=CF ∴AC=DF 在△ABC 和△DEF 中， AB DE BC EF AC DF∴△ABC≌△DEF（SSS） （2）由（1）可知，∠F=∠ACB ∵∠A=55°，∠B=88° ∴∠ACB=180°－（∠A+∠B）=180°－（55°+88°）=37° ∴∠F=∠ACB=37° 3．（2019·辽宁中考模拟）已知：如图，点 A、D、C、B 在同一条直线上，AD=BC，AE=BF，CE=DF，求 证：AE∥BF． 【答案】证明见解析. 【解析】 ∵AD=BC，∴AC=BD， 在△ACE 和△BDF 中， ＝ t ＝ t ＝ ， ∴△ACE≌△BDF（SSS） ∴∠A=∠B， ∴AE∥BF； 知识点 3 角平分线 角平分线的性质定理：角平分线上的点到角两边的距离相等； 判定定理：到角两边距离相等的点在角的平分线上． 三角形中角平分线的性质：三角形的三条角平分线相交于一点，并且这点到三条边距离相等。 考查题型十二 图中有角平分线，向两边作垂线 1.（2019·襄樊市月考）在△ABC 中，AD 是∠BAC 的平分线，E、F 分别为 AB、AC 上的点，且∠EDF+∠EAF=180°， 求证 DE=DF． 【答案】证明见解析. 【详解】 过 D 作 DM⊥AB 于 M，DN⊥AC 于 N， 即∠EMD=∠FND=90°， ∵AD 平分∠BAC，DM⊥AB，DN⊥AC， ∴DM=DN（角平分线性质）， ∵∠EAF+∠EDF=180°， ∴∠MED+∠AFD=360°-180°=180°， ∵∠AFD+∠NFD=180°， ∴∠MED=∠NFD， 在△EMD 和△FND 中 t 헀 t 헀 헀 ， ∴△EMD≌△FND（AAS）， ∴DE=DF． 2.（2019·襄樊市月考）在△ABC 中，AD 是∠BAC 的平分线，E、F 分别为 AB、AC 上的点，且∠EDF+∠EAF=180°， 求证 DE=DF． 【答案】证明见解析. 【详解】 过 D 作 DM⊥AB 于 M，DN⊥AC 于 N， 即∠EMD=∠FND=90°， ∵AD 平分∠BAC，DM⊥AB，DN⊥AC， ∴DM=DN（角平分线性质）， ∵∠EAF+∠EDF=180°， ∴∠MED+∠AFD=360°-180°=180°， ∵∠AFD+∠NFD=180°， ∴∠MED=∠NFD， 在△EMD 和△FND 中 t 헀 t 헀 헀 ， ∴△EMD≌△FND（AAS）， ∴DE=DF． 3．（2017·广东中考模拟）如图，OC 是∠AOB 的平分线，P 是 OC 上一点，PD⊥OA 于点 D，PD=6，则点 P 到边 OB 的距离为_____． 【答案】6 【解析】 作 PE⊥OB 于 E，如图， ∵OC 是∠AOB 的平分线，PD⊥OA，PE⊥OB， ∴PE=PD=6， 即点 P 到边 OB 的距离为 6． 故答案为 6． 考查题型十三 角平分线加垂线，三线合一试试看 1.如图，已知 AE⊥FE，垂足为 E，且 E 是 DC 的中点． (1)如图①，如果 FC⊥DC，AD⊥DC，垂足分别为 C，D，且 AD＝DC，判断 AE 是∠FAD 的角平分线吗？(不必 说明理由) (2)如图②，如果(1)中的条件“AD＝DC”去掉，其余条件不变，(1)中的结论仍成立吗？请说明理由； (3)如图③，如果(1)中的条件改为“AD∥FC”，(1)中的结论仍成立吗？请说明理由． 【答案】（1）AE 是∠FAD 的角平分线（2）成立（3）成立 【详解】 （1）AE 是∠FAD 的角平分线； （2）成立，如图，延长 FE 交 AD 于点 B， ∵E 是 DC 的中点， ∴EC=ED， ∵FC⊥DC，AD⊥DC， ∴∠FCE=∠EDB=90°， 在△FCE 和△BDE 中， t t t t t t , ∴△FCE≌△BDE， ∴EF=EB， ∵AE⊥FE， ∴AF=AB， ∴AE 是∠FAD 的角平分线； （3）成立，如图，延长 FE 交 AD 于点 B， ∵AD=DC， ∴∠FCE=∠EDB， 在△FCE 和△BDE 中， t t t t t t , ∴△FCE≌△BDE， ∴EF=EB， ∵AE⊥FE， ∴AF=AB， ∴AE 是∠FAD 的角平分线. 考查题型十四 角平分线平行线，等腰三角形来填 1.（2017 春 赣州市期末）如图，在△ABC 中，∠ABC 与∠ACB 的平分线交于点 O，过点 O 作 DE//BC，分别 交 AB,AC 于点 D,E,若 AB=4，AC=3，则△ADE 的周长是_______________。 【答案】7 【解析】 解：∵BO 平分∠ABC， ∴∠DBO=∠CBO， ∵DE∥BC， ∴∠CBO=∠DOB， ∴∠DBO=∠DOB， ∴BD=DO， 同理 OE=EC， ∴△ADE 的周长=AD+AE+ED=AB+AC=4+3=7． 故答案为：7． 2.（2018·江苏中考模拟）如图，AB∥CD，CB 平分∠ACD，∠ABC=35°，则∠BAE=__________度. 【答案】70 【详解】∵AB∥CD，∠ABC=35°， ∴∠BCD=∠B=35°， ∵CB 平分∠ACD， ∴∠BAE=2∠BCD=70° 故正确答案为：70. 考查题型十五 图形对折问题 1．（2017 丹阳市月考）如图 a 是长方形纸带，∠DEF=25°，将纸带沿 EF 折叠成图 b，再沿 BF 折叠成图 c， 则图 c 中的∠CFE 的度数是____________°． 【答案】105° 【解析】 由图 a 知，∠EFC=155°. 图 b 中，∠EFC=155°，则∠GFC=∠EFC-∠EFG=155°-25°=130°. 图 c 中，∠GFC=130°，则∠CFE=130°-25°=105°. 故答案为：105°. 2.（2019 道外区期末）如图 a 是长方形纸带（提示：AD∥BC），将纸带沿 EF 折叠成图 b，再沿 GF 折叠成图 c． （1）若∠DEF＝20°，则图 b 中∠EGB＝______，∠CFG＝______； （2）若∠DEF＝20°，则图 c 中∠EFC＝______； （3）若∠DEF＝α，把图 c 中∠EFC 用α表示为______； （4）若继续按 EF 折叠成图 d，按此操作，最后一次折叠后恰好完全盖住∠EFG，整个过程共折叠了 9 次， 问图 a 中∠DEF 的度数是多少． 【答案】（1）40°，140°；（2）120°；（3）180°﹣3α；（4）18°． 【详解】 （1）∵长方形的对边是平行的， ∴∠BFE＝∠DEF＝20°， ∴∠EGB＝∠BFE+∠DEF＝40°， ∴∠FGD＝∠EGB＝40°， ∴∠CFG＝180°﹣∠FGD＝140°； 故答案为：40°，140°； （2）∵长方形的对边是平行的， ∴∠BFE＝∠DEF＝20°， ∴图 a、b 中的∠CFE＝180°﹣∠BFE，以下每折叠一次，减少一个∠BFE， ∴图 c 中的∠EFC 度数是 120°； 故答案为：120°； （3）由（2）中的规律，可得∠CFE＝180°﹣3α． 故答案为：180°﹣3α； （4）设图 a 中∠DEF 的度数是 x°， 由（2）中的规律，可得 180﹣(9+1)x＝0． 解得：x＝18． 故答案为：18°． 考查题型十六 角平分线与实际问题 1．（2019·深圳市文锦中学中考模拟）已知：如图所示，三条公路两两分别相交于点 A、B、C，在甲区内求 作一点 P，使点 P 到三条公路的距离都相等。 【答案】答案见解析 【详解】 解：点 P 位置如图所示：