2008年福建省高考数学试卷(理科)【附答案、word版本,可再编辑;B4纸型两栏】
2008年福建省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1. 若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为( )
A.1 B.2 C.1或2 D.-1
2. 设集合A={x|xx-1<0},B={x|0
0x≤2则yx的取值范围是( )
A.(0, 2) B.(0, 2) C.(2, +∞) D.[32, +∞)
9. 函数f(x)=cosx(x∈R)的图象按向量(m, 0)平移后,得到函数y=-f'(x)的图象,则m的值可以为( )
A.π2 B.π C.-π D.-π2
10. 在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2-b2)tanB=3ac,则角B的值为( )
A.π6 B.π3 C.π6或5π6 D.π3或2π3
11. 双曲线x2a2-y2b2=1(a>0, b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为( )
A.(1, 3) B.(1, 3] C.(3, +∞) D.[3, +∞]
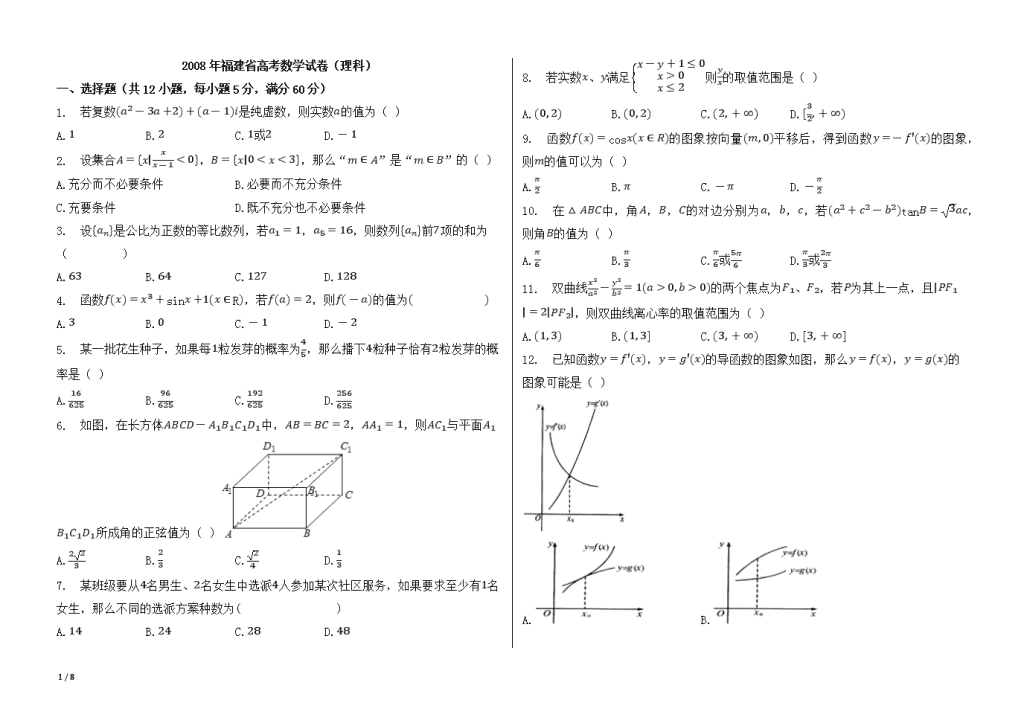
12. 已知函数y=f'(x),y=g'(x)的导函数的图象如图,那么y=f(x),y=g(x)的图象可能是( )
A. B.
8 / 8
C. D.
二、填空题(共4小题,每小题4分,满分16分)
13. 若(x-2)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4+a5=________.(用数字作答)
14. 若直线3x+4y+m=0与曲线x=1+cosθ,y=-2+sinθ,(θ为参数)没有公共点,则实数m的取值范围是________.
15. 若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是________.
16. 设P是一个数集,且至少含有两个数,若对任意a,b∈P,都有a+b,a-b,ab,ab∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域;数集F={a+b2|a, b∈Q}也是数域.有下列命题:
①整数集是数域;
②若有理数集Q⊆M,则数集M必为数域;
③数域必为无限集;
④存在无穷多个数域.
其中正确的命题的序号是________.(把你认为正确的命题的序号填填上)
三、解答题(共6小题,满分74分)
17. 已知向量m→=(sinA,cosA),n→=(1,-2),且m→⋅n→=0.
(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx,(x∈[0,π4])的值域.
18. 如图,在四棱锥P-ABCD中,则面PAD⊥底面ABCD,侧棱PA=PD=2,底面ABCD为直角梯形,其中BC // AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的大小;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为32?若存在,求出AQQD的值;若不存在,请说明理由.
8 / 8
19. 已知函数f(x)=13x3+x2-2.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an, an+12-2an+1)(n∈N*)在函数y=f'(x)的图象上,求证:点(n, Sn)也在y=f'(x)的图象上;
(2)求函数f(x)在区间(a-1, a)内的极值.
20. 某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为23,科目B每次考试成绩合格的概率均为12.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的数学期望Eξ.
8 / 8
21. 如图,椭圆x2a2+y2b2=1(a>b>0)的一个焦点是F(1, 0),O为坐标原点.
(1)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(2)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有|OA|2+|OB|2<|AB|2,求a的取值范围.
22. 已知函数f(x)=ln(1+x)-x
(1)求f(x)的单调区间;
(2)记f(x)在区间[0, n](n∈N*)上的最小值为bn令an=ln(1+n)-bn
(I)如果对一切n,不等式an10或m<0
15.9π
16.③④
三、解答题(共6小题,满分74分)
17.解:(1)m→⋅n→=sinA-2cosA=0即sinA=2cosA
∴ tanA=2
(2)f(x)=cos2x+tanAsinx=cos2x+2sinx=1-2sin2x+2sinx
令sinx=t
∵ x∈[0,π4]∴ t∈[0,22]
∴ y=-2t2+2t+1=-2(t-12)2+32,∴ t∈[0,22]
∴ 当t=12时,y最大为32;当t=0时,y最小为1
域为[1, 32].
18.解:(1)证明:在△PAD中,PA=PD,O为AD的中点,所以PO⊥AD
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD
所以PO⊥平面ABCD.
(2)连接BO,在直角梯形ABCD中,BC // AD,AD=2AB=2BC=2有OD // BC
且OD=BC,所以四边形OBCD是平行四边形,所以OB // DC
由(1)知PO⊥OB,∠PBC是锐角,
所以∠PBC是异面直线PB与CD所成的角
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=2
在Rt△AOP中 因为AP=2AO=1,所以OP=1
在Rt△AOP中tan∠PBC=PCBC=12=22,∠PBC=arctan22
所以:异面直线PB与CD所成角的大小arctan22.
(3)假设存在点Q,使得它到平面PCD的距离为32.
设QD=x,则S△DQC=12x,由(2)得CD=OB=2,
在Rt△POC中,PC=OC2+OP2=2,
所以PC=CD=DP,S△PCD=34⋅(2)2=32,
由Vp-DQC=VQ-PCD,得x=32,所以存在点Q满足题意,此时AQQD=13.
解法二:
8 / 8
(1)同解法一.
(2)以O为坐标原点,OC→、OD→、OP→的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz,
依题意,易得A(0, -1, 0),B(1, -1, 0),C(1, 0, 0),D(0, 1, 0),P(0, 0, 1),
所以CD→=(-1,1,0),PB→=(1,-1,-1).
所以异面直线PB与CD所成的角是arccos63,
(3)假设存在点Q,使得它到平面PCD的距离为32,
由(2)知CP→=(-1,0,1),CD→=(-1,1,0).
设平面PCD的法向量为n=(x0, y0, z0).
则n⋅CP→=0n⋅CD→=0所以-x0+z0=0-x0+y0=0即x0=y0=z0,
取x0=1,得平面PCD的一个法向量为n→=(1, 1, 1).
设Q(0,y,0)(-1≤y≤1),CQ→=(-1,y,0),由|CQ⋅n→||n|=32,得|-1+y||3|=32,
解y=-12或y=52(舍去),
此时|AQ|=12,|QD|=32,所以存在点Q满足题意,此时AQQD=13.
19.解:(1)证明:因为f(x)=13x3+x2-2,所以f'(x)=x2+2x,
由点(an, an+12-2an+1)(n∈N+)在函数y=f'(x)的图象上,
又an>0(n∈N+),所以(an-1-an)(an+1-an-2)=0,
所以Sn=3n+n(n-1)2×2=n2+2n,又因为f'(n)=n2+2n,所以Sn=f'(n),
故点(n, Sn)也在函数y=f'(x)的图象上.
(2)解:f'(x)=x2+2x=x(x+2),由f'(x)=0,得x=0或x=-2.
当x变化时,f'(x)﹑f(x)的变化情况如下表:
x
(-∞, -2)
-2
(-2, 0)
0
(0, +∞)
f'(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
注意到|(a-1)-a|=1<2,从而
①当,此时f(x)无极小值;
②当a-1<01),
因此,恒有|OA|2+|OB|2<|AB|2.
(2)当直线AB不与x轴重合时,
设直线AB的方程为:x=my+1,代入x2a2+y2b2=1,
整理得(a2+b2m2)y2+2b2my+b2-a2b2=0,
所以y1+y2=-2b2ma2+b2m2,y1y2=b2-a2b2a2+b2m2
因为恒有|OA|2+|OB|2<|AB|2,所以∠AOB恒为钝角.
即OA→⋅OB→=(x1,y1)⋅(x2,y2)=x1x2+y1y2<0恒成立.
x1x2+y1y2=(my1+1)(my2+1)+y1y2=(m2+1)y1y2+m(y1+y2)+1
=(m2+1)(b2-a2b2)a2+b2m2-2b2m2a2+b2m2+1
=-m2a2b2+b2-a2b2+a2a2+b2m2<0.
又a2+b2m2>0,所以-m2a2b2+b2-a2b2+a2<0对m∈R恒成立,
即a2b2m2>a2-a2b2+b2对m∈R恒成立.
当m∈R时,a2b2m2最小值为0,所以a2-a2b2+b2<0.
a20,b>0,所以a<b2,即a2-a-1>0,
解得a>1+52或a<1-52(舍去),即a>1+52,
综合(1)(II),a的取值范围为(1+52, +∞).
22.解:(1)因为f(x)=ln(1+x)-x,所以函数定义域为(-1, +∞),且f'(x)=11+x-1=-x1+x.
由f'(x)>0得-10,f(x)的单调递减区间为(0, +∞).
(2)因为f(x)在[0, n]上是减函数,所以bn=f(n)=ln(1+n)-n,
则an=ln(1+n)-bn=ln(1+n)-ln(1+n)+n=n.
(I)因为can+21因此c≤1,即实数c的取值范围是(-∞, 1].
(II)由(I)知12n+1<2n+1-2n-1.
下面用数学归纳法证明不等式1⋅3⋅5⋅⋅(2n-1)2⋅4⋅6⋅⋅(2n)<12n+1(n∈N+)
①当n=1时,左边=12,右边=13,左边<右边.不等式成立.
②假设当n=k时,不等式成立.即1⋅3⋅5⋅⋅(2k-1)2⋅4⋅6⋅⋅(2k)<12n+1.
当n=k+1时,1⋅3⋅5⋅…(2k-1)(2k+1)2⋅4⋅6⋅…2k(2k+2)<12k+1⋅2k+12k+2=2k+12k+2=2k+2˙⋅12k+3
8 / 8
=4k2+8k+34k2+8k+4⋅12k+3<12k+3=12(k+1)+1,
即n=k+1时,不等式成立
综合①、②得,不等式1⋅3⋅5⋅⋅(2n-1)2⋅4⋅6⋅⋅(2n)<12n+1(n∈N*)成立.
所以1⋅3⋅5⋅⋅(2n-1)2⋅4⋅6⋅⋅(2n)<2n+1-2n-1,
所以12+1⋅32⋅4+…+1⋅3⋅…⋅(2n-1)2⋅4⋅…⋅(2n)<3-1+5-3+...+2n+1-2n-1=2n+1-1.
即a1a2+a1a3a2a4++a1a3a2n-1a2a4a2n<2an+1-1(n∈N*).
8 / 8