2020届二轮复习直线的倾斜角与斜率课件（全国通用）

2020届二轮复习直线的倾斜角与斜率课件（全国通用）

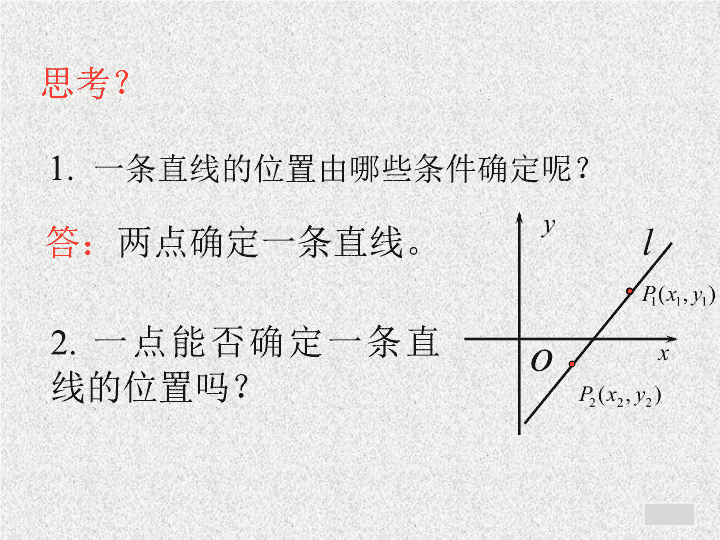
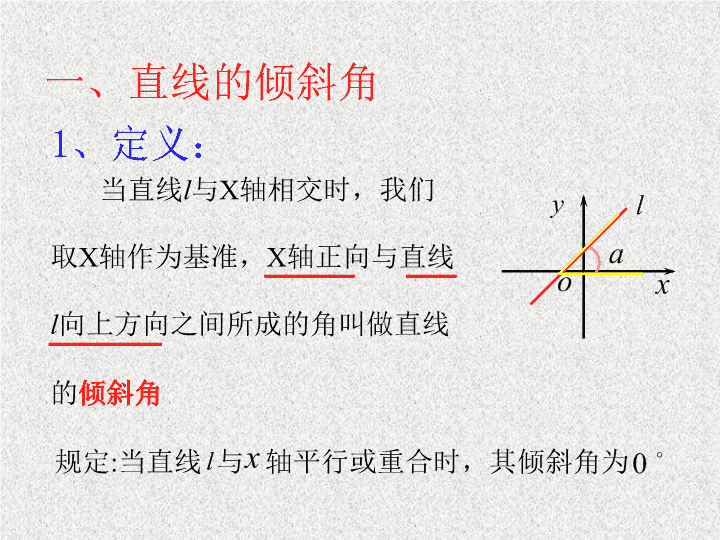
直线的倾斜角与斜率 思考？ 1. 一条直线的位置由哪些条件确定呢？ 2. 一点能否确定一条直线的位置吗？ 答： 两点确定一条直线。 一、直线的倾斜角 1 、 定义： 当直线 l 与 X 轴相交时，我们 取 X 轴作为基准， X 轴正向与直线 l 向上方向之间所成的角叫做直线 的 倾斜角 规定 : 当直线 与 轴平行或重合时，其倾斜角为 练习： x y o x y o x y o x y o （ A ） （ B ） （ C ） （ D ） 下列图中标出的直线的倾斜角对不对？如果不对，违背了定义中的哪一条？ 2 、 直线倾斜角的范围： 思考？ 直线的倾斜角范围是多少？ p o y x y p o x p o y x p o y x 0° ＜ ＜ 90° = 90° 90° ＜ ＜ 180° = 0° 零度角 锐角 直角 钝角 按倾斜角去分类，直线可分几类？ 2 、 直线倾斜角的范围： 答： 直线的倾斜角的取值范围为： 思考？ 直线的倾斜角范围是多少？ 二、直线的的斜率 日常生活中，我们经常用“升高量与前进量的 比”表示倾斜面的“坡度”（倾斜程度），即 二、直线的的斜率 升高量 前进量 A B C D 设直线的倾斜程度为 K 1 、 定义： 我们把一条直线的倾斜角 的正切值叫做这 条直线的 斜率。 用小写字母 k 表示，即： 思考 : 是否每条直线都有斜率 ? 4. 如果倾斜角是零度角 ? 1. 如果倾斜角是锐角 ? 2. 如果倾斜角是直角 ? 3. 如果倾斜角是钝角 ? 已知直线的倾斜角 , 求直线的斜率 1. 2. 3. 4. 5. 6. 7. 8. 练习 : 能不能构造一个直角三角形去求？ 3 、 探究：由两点确定的直线的斜率 如图，当 α 为锐角时， 倾斜角是锐角时 如图，当 α 为钝角是， 倾斜角是钝角时 1 、当 的位置对调时， 值又如何呢？ 思考？ x y o (3) y o x (4) 请同学们课后推导！ 思考？ 2 、当直线平行于 x 轴，或与 x 轴重合时，上述公式还适用吗？为什么？ 答：成立，因为分子为 0 ，分母不为 0 ， k =0 3 、当直线平行于 y 轴，或与 y 轴重合时，上述公式还适用吗？为什么？ 思考？ 答：不成立，因为分母为 0 。 4 、已知直线上两点 、 ， 运用上述公式计算直线 AB 的斜率时，与 A 、 B 的顺序有关吗？ 答：与 A 、 B 两点的顺序无关。 4 、直线的斜率公式： 综上所述，我们得到经过两点 的直线的斜率公式： 例 1 如图，已知 A(4,2) 、 B( － 8,2) 、 C(0, － 2) ， 求直线 AB 、 BC 、 CA 的斜率，并判断这些直线 的倾斜角是什么角？ y x o . . . . . . . . . . A B C 解：直线 AB 的斜率 直线 BC 的斜率 直线 CA 的斜率 ∵ ∴ 直线 CA 的倾斜角为锐角 ∴ 直线 BC 的倾斜角为钝角。 ∵ ∴ 直线 AB 的倾斜角为零度角。 ∵ 三、小结： 1 、直线的倾斜角定义及其范围： 2 、直线的斜率定义： 3 、斜率 k 与倾斜角 之间的关系： 4 、斜率公式： 作业： 课本 p86 练习 1.2.3 P89 习题 3.1 A 组 1 ， 2 谢谢 练习 （课本 p86 练习 3 ） 已知 a ， b ， c 是两两不相等的实数，求经过两点的直线倾斜角 A （ a ， c ） B （ b ， c ） C （ a ， b ） D （ a ， c ） P （ b ， b+c ） Q （ a ， c+a ） 练习（课本 p89 习题 3.1 A 组 4 ） m 为何值时，经过两点 A （ -m ， 6 ）， B （ 1 ， 3m ）的直线斜率是 12 ？ m 为何值时，经过两点 A （ m ， 2 ）， B （ -m ， -2m-1 ）的直线斜率的倾斜角是 60 ° ？