- 2021-04-13 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年吉林省长春外国语学校高二上学期期末考试数学试题(Word版)
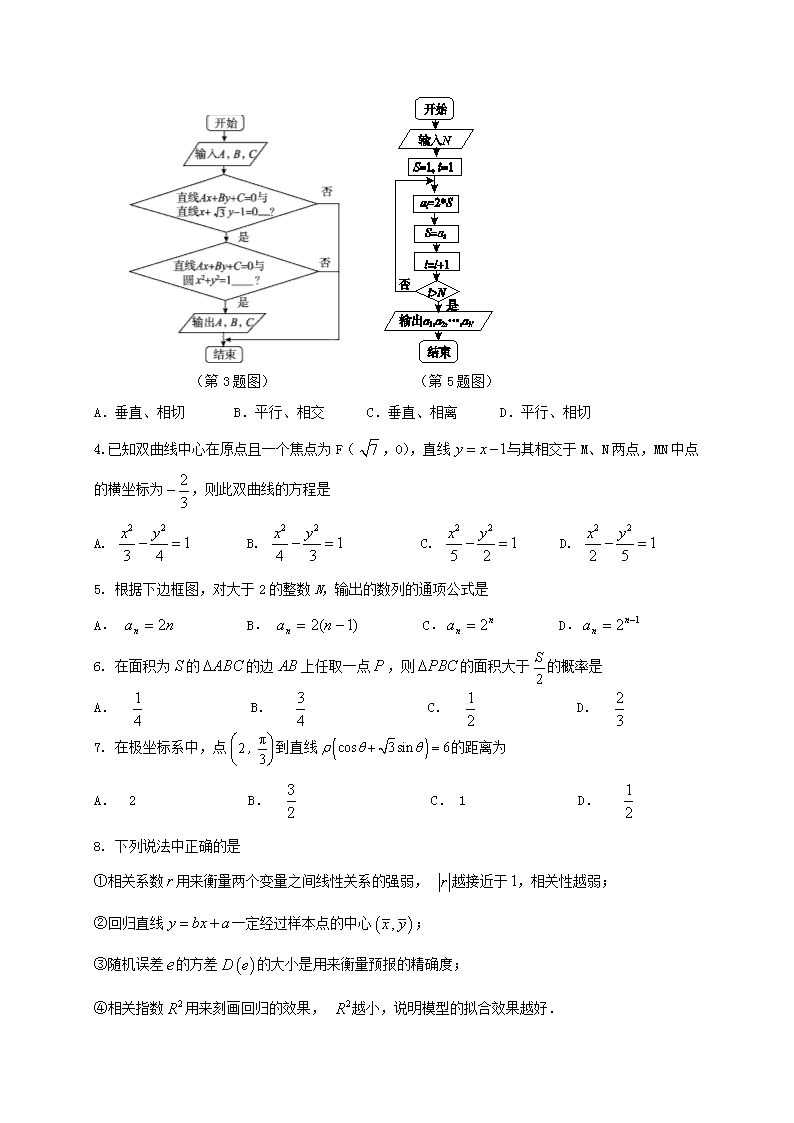
长春外国语学校2017-2018学年第一学期期末考试高二年级 数学试卷 出题人 : 刘 洋 审题人 : 宋志刚 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页。考试结束后,将答题卡交回。 注意事项: 1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信 息条形码粘贴区。 2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书 写,字体工整、笔迹清楚。 3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效; 在草稿纸、试题卷上答题无效。 4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。 5. 保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 第Ⅰ卷 一、选择题:本题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1. 已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于,则椭圆C的方程是 A. B. C. D. 2. 在直角坐标系中,点A(-2,2).以坐标原点为极点,轴正半轴为极轴建立极坐标系,点A的极坐标为 A. B. C. D. 3. 运行如图所示的程序框图,输出A,B,C的一组数据为,-1,2,则在两个判断框内的横线上分别应填 (第3题图) (第5题图) A.垂直、相切 B.平行、相交 C.垂直、相离 D.平行、相切 4. 已知双曲线中心在原点且一个焦点为F(,0),直线与其相交于M、N两点,MN中点的横坐标为,则此双曲线的方程是 A. B. C. D. 5. 根据下边框图,对大于2的整数N,输出的数列的通项公式是 A. B. C. D. 6. 在面积为的的边上任取一点,则的面积大于的概率是 A. B. C. D. 7. 在极坐标系中,点到直线的距离为 A. 2 B. C. 1 D. 8. 下列说法中正确的是 ①相关系数用来衡量两个变量之间线性关系的强弱, 越接近于,相关性越弱; ②回归直线一定经过样本点的中心; ③随机误差的方差的大小是用来衡量预报的精确度; ④相关指数用来刻画回归的效果, 越小,说明模型的拟合效果越好. A. ①② B. ③④ C. ①④ D. ②③ 9. 下列程序执行后输出的结果是 A. 600 B. 880 C. 990 D. 1100 10. 已知双曲线的右焦点为,直线与双曲线的渐近线在第一象限的交点为为坐标原点,若的面积为,则双曲线的离心率为 A. B. C. D. 11. 设不等式组表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是 A. B. C. D. 12. 已知直线(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,设点的直角坐标为,直线与曲线C 的交点为,,的值为 A. 16 B. 18 C. 8 D. 10 第Ⅱ卷 二、填空题:本题共4小题,每小题5分。 13. 直线:与圆C:x2+(y-1)2=5的位置关系是______________. 14. 过抛物线的焦点的直线交抛物线于P(x1,y1),Q(x2,y2)两点,如果x1+x2=6,则PQ=________. 15. 曲线的参数方程为(为参数), 曲线的直角坐标方程为_______________. 16. 一圆形纸片的半径为,圆心为,为圆内一定点, , 为圆周上任意一点,把圆纸片折叠,使与重合,然后抹平纸片,这样就得到一条折痕,设与交于点,以所在直线为轴,线段的中垂线为轴,建立直角坐标系,则点的轨迹方程为__________. 三、解答题:本题共70分,其中17题10分,18至22题每题12分. 17.下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据. (1) 请根据上表提供的数据,用最小二乘法求出y关于x的回归方程; (2) 已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5) 18. 以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示. (Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差; (Ⅱ)如果X=9,分别从甲、乙两组中各随机选取一名同学,求这两名同学的植树总棵数为19的概率. 19. 已知曲线C的极坐标方程是ρ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线的参数方程是(t为参数),求直线与曲线C相交所截的弦长. 20. 4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”, (1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率) (2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关: 懒虫 书虫 合计 男 15 女 45 合计 P(K2≥k0) 0.100 0.050 0.025 0.010 0.001 k0 2.706 3.841 5.024 6.635 10.828 21. 在平面直角坐标系xOy中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为. (1)求曲线C1的直角坐标方程; (2)曲线C2的方程为+=1,设P,Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值. 22. 已知椭圆的离心率为,且椭圆上一点与椭圆左右两个焦点构成的三角形周长为. (1)求椭圆的方程; (2)如图,设点为椭圆上任意一点,直线和椭圆交于两点,且直线与轴分别交于两点,求证: . 1.B 2.B 3.A4.D5.C6.C 7.C8.D9.C 10.B 11.D 12.B 13.相交. 14.抛物线y2=4x的焦点为F(1,0),准线方程为x=-1.根据题意可得,PQ=PF+QF=x1+1+x2+1=x1+x2+2=8. 15.. 16.. 三、解答题 17. 解 (1)==4.5, 1分 ==3.5, 1分 xiyi=3×2.5+4×3+5×4+6×4.5=66.5,x=32+42+52+62=86, ∴== 6分 =0.7, =-=3.5-0.7×4.5=0.35. 8分 ∴所求的回归方程为=0.7x+0.35. (2)现在生产100吨甲产品用煤 =0.7×100+0.35=70.35, ∴90-70.35=19.65. ∴生产能耗比技改前降低约19.65吨标准煤. 10分 18. 19. 20. (1)由已知可得:(0.01+0.02+0.03+x+0.015)×10=1,可得x=0.025. 2分 因为(0.025+0.015)×10=0. 4,将频率视为概率,由此可以估算出全校3000名学生中“书虫”大概有1200人. 4分 (2)完成下面的2×2列联表如下: 懒虫 书虫 合计 男 40 15 55 女 20 25 45 合计 60 40 100 7分 K2=≈8.249. 10分 由8.249>6.635,故在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关. 12分 21. 22.查看更多