上海市嘉定区封浜高中2019-2020学年高二下学期期末考试数学试题

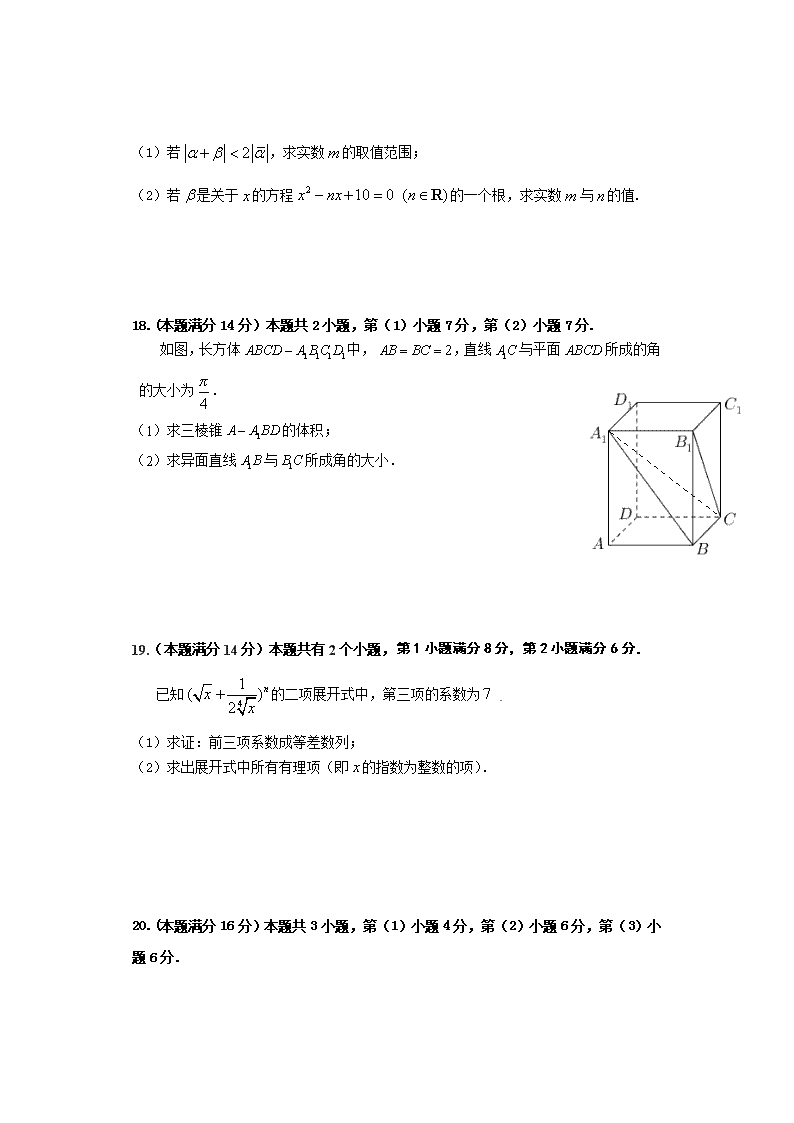
上海市嘉定区封浜高中2019-2020学年高二下学期期末考试数学试题

上海市嘉定区2019学年第二学期封浜高级中学高二年级数学期末质量调研（满分150分，时间120分钟）‎ 一.填空题（本大题满分54分）本大题共有12题，1-6每题4分，7-12每题5分考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得分，否则一律得零分.‎ ‎1．抛物线的焦点坐标为 . ‎ ‎2．平面直角坐标系中点到直线的距离为 ． ‎ ‎3．若复数满足（是虚数单位），则的虚部是 . ‎ ‎4．世界杯小组赛，从四支队伍中出线两支队伍，则出线队伍共有 种不同的组合． ‎ ‎5．侧棱长为,底面面积为的正四棱柱的体对角线的长为 . ‎ ‎6．双曲线的两条渐近线的夹角大小为 . ‎ ‎7．底面半径和高均为的圆柱的表面积为 ． ‎ ‎8．双曲线的虚轴长是实轴长的倍，则 ． ‎ ‎9．已知空间直角坐标系中，某二面角的大小为，，半平面和的一个法向量分别为，，则 ．(结果用反三角函数值表示) ‎ ‎10．二项式的展开式中各项系数的和是 ． ‎ ‎11．有一个倒圆锥形的容器，它的底面半径是5厘米，高是10厘米，容器内放着49个半径为1厘米的玻璃球，在向容器倒满水后，再把玻璃球全部取出，则此时容器内水面的高度 为 厘米．‎ ‎12．已知定点，点在抛物线上运动，若复数 在复平面内分别对应点的位置，且，则的最小值为 ． ‎ 二.选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.‎ ‎13．空间内，异面直线所成角的取值范围是……………………………………（ ）．‎ ‎(A) (B) (C) (D) ‎ ‎14.“”是“直线与直线相互垂直”的 ……………………………………………………………………………（ ）.‎ ‎（A）充分而不必要条件 （B）必要而不充分条件 ‎（C）充要条件 （D）既不充分也不必要条件 ‎15．曲线的图像………………………………………………( )．‎ ‎(A)关于轴对称 (B)关于原点对称，但不关于直线对称 ‎(C)关于轴对称 (D)关于直线对称，也关于直线对称 ‎16．下列命题中，正确的命题是……………………………………………………( )．‎ ‎ (A) 若、，，则． ‎ ‎(B) 若，则不成立． ‎ ‎(C) ，，则或．‎ ‎(D) ，，则且．‎ 三．解答题（本大题满分76分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎17. （本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．‎ 已知复数，，.‎ ‎（1）若，求实数的取值范围；‎ ‎（2）若是关于的方程的一个根，求实数与的值.‎ ‎ ‎ ‎18.(本题满分14分）本题共2小题，第（1）小题7分，第（2）小题7分.‎ 如图，长方体中，，直线与平面所成的角的大小为．‎ ‎（1）求三棱锥的体积；‎ ‎（2）求异面直线与所成角的大小．‎ ‎19.（本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分．‎ 已知的二项展开式中，第三项的系数为．‎ ‎（1）求证：前三项系数成等差数列；‎ ‎（2）求出展开式中所有有理项（即的指数为整数的项）．‎ ‎20.(本题满分16分）本题共3小题，第（1）小题4分，第（2）小题6分，第（3）小题6分.‎ 已知椭圆的左右顶点分别是，点在椭圆上．过该椭圆上任意一点作轴，垂足为，点在的延长线上，且．‎ ‎（1）求椭圆的方程；‎ ‎（2）求动点的轨迹的方程；‎ ‎（3）设直线（点不同于）与直线交于，为线段的中点，证明：直线与曲线相切．‎ ‎21. (本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．‎ 在平面直角坐标系中，为坐标原点．已知曲线上任意一点（其中）到定点的距离比它到轴的距离大1.‎ ‎（1）求曲线的轨迹方程；‎ ‎（2）若过点的直线与曲线相交于不同的两点，求的值；‎ ‎（3）若曲线上不同的两点、满足求的取值范围．‎ ‎2019学年第二学期高二期末质量调研 数学答案 ‎（满分150分，时间120分钟）‎ 考生注意：‎ ‎1．答卷前，考生务必在答题纸上将学校、班级、考试号、姓名等填写清楚．‎ ‎2．请按照题号在答题纸各题答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ ‎3．本试卷共有21道试题，可以使用规定型号计算器．‎ 一.填空题（本大题满分54分）本大题共有12题，1-6每题4分，7-12每题5分考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得分，否则一律得零分.‎ ‎1．抛物线的焦点坐标为 . ‎ ‎2．平面直角坐标系中点到直线的距离为 ． ‎ ‎3．若复数满足（是虚数单位），则的虚部是 . ‎ ‎4．世界杯小组赛，从四支队伍中出线两支队伍，则出线队伍共有 种不同的组合．‎ ‎5．侧棱长为,底面面积为的正四棱柱的体对角线的长为 . ‎ ‎6．双曲线的两条渐近线的夹角大小为 . ‎ ‎7．底面半径和高均为的圆柱的表面积为 ．‎ ‎8．双曲线的虚轴长是实轴长的倍，则 ．‎ ‎9．已知空间直角坐标系中，某二面角的大小为，，半平面和的一个法向量分别为，，则 ．(结果用反三角函数值表示) ‎ ‎10．二项式的展开式中各项系数的和是 ．‎ ‎11．有一个倒圆锥形的容器，它的底面半径是5厘米，高是10厘米，容器内放着49个半径为1厘米的玻璃球，在向容器倒满水后，再把玻璃球全部取出，则此时容器内水面的高度为 厘米．6‎ ‎12．已知定点，点在抛物线上运动，若复数在复平面内分别对应点的位置，且，则的最小值为 ． ‎ 二.选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.‎ ‎13．空间内，异面直线所成角的取值范围是……………………………………（ B ）．‎ ‎(A) (B) (C) (D) ‎ ‎14.“”是“直线与直线相互垂直”的 ……………………………………………………………………………（ A ）.‎ ‎（A）充分而不必要条件 （B）必要而不充分条件 ‎（C）充要条件 （D）既不充分也不必要条件 ‎15．曲线的图像………………………………………………( )．‎ ‎(A)关于轴对称 (B)关于原点对称，但不关于直线对称 ‎(C)关于轴对称 (D)关于直线对称，也关于直线对称 ‎16．下列命题中，正确的命题是……………………………………………………( )．‎ ‎ (A) 若、，，则． ‎ ‎(B) 若，则不成立． ‎ ‎(C) ，，则或．‎ ‎(D) ，，则且．‎ 三．解答题（本大题满分76分）‎ 本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎17. （本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．‎ 已知复数，，.‎ ‎（1）若，求实数的取值范围；‎ ‎（2）若是关于的方程的一个根，求实数与的值.‎ 解: （1） ………………………………………………………………2分 于是 …………………………4分 又 ，所以 ，解得：. …………6分 所以实数的取值范围为. …………………………………………………7分 ‎（2）因为（）是方程的一个根，‎ ‎（）也是此方程的一个根，…………………………………………9分 于是 …………………………………………………11分 ‎ 解得 或，且满足……………………13分 所以或 ……………………………………………………………14分 ‎18.(本题满分14分）本题共2小题，第（1）小题7分，第（2）小题7分.‎ 如图，长方体中，，直线与平面所成的角的大小为．‎ ‎（1）求三棱锥的体积；‎ ‎（2）求异面直线与所成角的大小．‎ 解：（1）联结，‎ 因为，‎ 所以就是直线与平面所成的角，………………………………2分 所以，所以 ……………………………………………4分 所以…………………………………………7分 ‎（2）联结，‎ 因为，所以 所以就是异面直线与所成的角或其补角………………………10分 在△中，‎ 所以……………………………………………………………13分 所以异面直线与所成角的大小是…………………………………14分 ‎19.（本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分．‎ 已知的二项展开式中，第三项的系数为．‎ ‎（1）求证：前三项系数成等差数列；‎ ‎（2）求出展开式中所有有理项（即的指数为整数的项）．‎ 解：（1）…………………………………2分 ‎，……………………………………………4分 所以前三项分别为，，‎ ‎……………………………………………………7分 所以前三项系数分别为，即前三项系数成等差数列……………………8分 ‎（2）……………10分 时，展开式中的指数为整数，‎ 所以展开式中所有有理项为：、、……………………………………………………………14分 ‎20.(本题满分16分）本题共3小题，第（1）小题4分，第（2）小题6分，第（3）小题6分.‎ 已知椭圆的左右顶点分别是，点在椭圆上．过该椭圆上任意一点作轴，垂足为，点在的延长线上，且．‎ ‎（1）求椭圆的方程；‎ ‎（2）求动点的轨迹的方程；‎ ‎（3）设直线（点不同于）与直线交于，为线段的中点，证明：直线与曲线相切．‎ 解：（1）由题意可知且，………………………………2分 所以椭圆方程为……………………………………………………………4分 ‎（2）设，则由可得， ………………………………6分 又在椭圆上，可知，……………………………9分 所以动点的轨迹的方程是……………………………………………10分 ‎（3）设，，由题意可知三点共线，所以，‎ 因为，，则，即，‎ ‎…………………………………………………………………………12分 ‎，从而，又，‎ 故 ‎ …………………………………14分 则圆心到直线的距离 …………………………………15分 所以直线与曲线相切 …………………………………………………………16分 ‎21. (本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．‎ 在平面直角坐标系中，为坐标原点．已知曲线上任意一点（其中）到定点的距离比它到轴的距离大1.‎ ‎（1）求曲线的轨迹方程；‎ ‎（2）若过点的直线与曲线相交于不同的两点，求的值；‎ ‎（3）若曲线上不同的两点、满足求的取值范围．‎ 解：（1）依题意知，动点到定点的距离等于到直线的距离，曲线是以原点为顶点，为焦点的抛物线………2分 ‎　∵ ∴　∴　曲线方程是…………………4分 ‎（2）当平行于轴时，其方程为，由解得、‎ 此时…………………………………………………6分 当不平行于轴时，设其斜率为，‎ 则由 得 设则有，……………………8分 ‎∴‎ ‎……………………………10分 ‎（3）设 ‎ ‎∴ ………………………………12分 ‎∵‎ ‎∴‎ ‎∵，化简得………………………………14分 ‎∴……………………………………14分 当且仅当 时等号成立………………………………16分 ‎∵‎ ‎∴当的取值范围是………18分