数学理卷·2018届云南省峨山彝族自治县第一中学高三上学期期末考试仿真(2018
2017-2018 学年上学期高三期末考试仿真测试卷
理科数学
一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 已知集合 , ,则 等于
A. B. C. D.
2. 已知 是虚数单位,若 是纯虚数,则实数
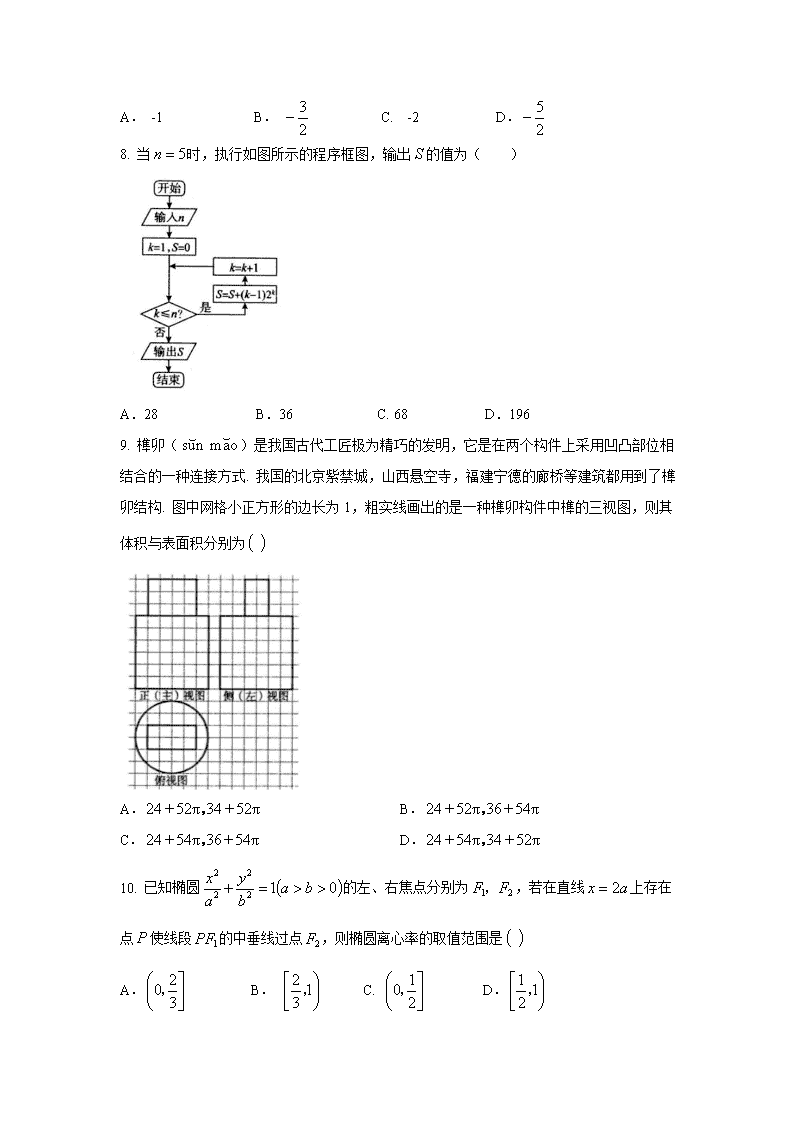
A.1 B.-1 C.2 D.-2
3. 已知向量 满足 , , ,则
A. B.3 C.5 D.9
4. 已知直线 平分圆 的周长,且直线 不经过第三象限,则直
线 的倾斜角 的取值范围为
A. B. C. D.
5. 将函数 的图象上各点的横坐标伸长到原来的 2 倍,再向左平移 个
单位,所得图象的一条对称轴的方程是
A. B. C. D.
6. 函数 的图象大致是
7. 若 , 展开式中, 的系数为-20,则 等于
2{ 2 0 }Z= + − ≤ ∈A x x x x, { 2 }Z= ∈B = x x k k, BA ( )
{ }10, { }24 −− , { }01,− { }02,−
i
2i + i= 1+i
az ( )=a
ba, 2=a 1=b 2−=⋅ba ( )=+ ba2
5
l 0266: 22 =++−+ yxyxC l
l θ ( )
[ ] 13590 , [ ] 12090 , [ ] 13560 , [ ] 15090 ,
π( ) sin 2 4
f x = x - π
12
( )
3π= 16x 7π= 24x 2π= 3x 5π= 6x
cos 3π 3π( ) = - 0 0-sin 2 2
∈ ∪
xf x xx x
, , , ( )
0
>=+ bab
y
a
x
21 FF, ax 2=
P 1PF 2F ( )
3
20,
13
2,
2
10,
12
1,
11. 已知 ,且 ,则
A. B. C. D.
12. 已知函数 若关于 的方程 至少有两个不
同的实数解,则实数 的取值范围为( )
A. B.
C. D.
二、填空题:本小题 4 小题,每小题 5 分,共 20 分.
13. 在 1,2,3,4,5,6,7,8 中任取三个不同的数,取到 3 的概率为 .
14. 已知 的面积为 ,角 的对边分别为 ,若 ,
, ,则 .
15. 已知函数 是偶函数,定义域为 ,且 时, ,则
曲线 在点 处的切线方程为 .
16.已知正方体 的体积为 1,点 在线段 上(点 异于点 ) ,
点 为线段 的中点,若平面 截正方体 所得的截面为四边形,
则线段 长的取值范围为 .
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17-21 题为必考题,每
个试题考生都必须作答.第 22、23 题为选考题,考生根据要求作答.
(一)必考题:共 60 分
17. 已知 是等比数列, 满足 ,且
.
(Ⅰ)求 的通项公式和前 项和 ;
π0 2
∈ θ , 35cos
12
sin
12 =+ θθ
( )=θ2tan
24
7
7
24
24
7±
7
24±
( )
≤++−
>+−=
,,
,,
0211
022
xmx
xmmxxxf x 0)( =− mxxf
m
( )∞+
− ,, 203
1
( )∞+
− ,, 113
1
∞+− ,
3
1 ( )∞+
− ,, 223
1
ABC∆ S CBA ,, cba ,, CS cos4=
2=a 23=b =C
( )xf ( ) ( )∞+∞− ,, 00 0>x 1( ) ex
x -f x =
( )xfy = ( )( )11 −− f,
1111 DCBAABCD − M BC M CB,
N 1CC AMN 1111 DCBAABCD −
BM
{ }na { }nb 31 21 == bb ,
( ) n
nn nbababa 23232211 ⋅−+=+++
{ }na n nS
(Ⅱ)求 的通项公式.
18. 随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,
聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区 18∽50 岁的 5000 名
居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
(Ⅰ)以频率估计概率,若在该地区任取 3 位居民,其中恰有 位居民的月流量的使用情况
在 300M-400M 之间,求 的期望 ;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况 与其日销售份数 成线性相
关关系,该研究人员将流量套餐的打折情况 与其日销售份数 的结果统计如下表所示:
折扣 1 折 2 折 3 折 4 折 5 折
{ }nb
X
X ( )XE
x y
x y
x
销售份数 50 85 115 140 160
试建立 关于 的的回归方程.
附注:回归方程 中斜率和截距的最小二乘估计公式分别为:
,
19. 在四棱锥 中,底面 是矩形, 平面 , 是等腰三角
形, , 是 的一个三等分点(靠近点 ), 与 的延长线交于点 ,
连接 .
(Ⅰ)求证:平面 平面 ;
(Ⅱ)求二面角 的正切值
y
y x
axby ˆˆˆ +=
( )( )
( )∑
∑
−
−
−
−−
= n
i
i
N
i
ii
xx
yyxx
b
1
2
1ˆ xbya ˆˆ −=
ABCDP − ABCD ⊥PA ABCD PAD∆
ADAB 2= E AB A CE DA F
PF
⊥PCD PAD
FPEA −−
20. 过抛物线 的焦点 作直线 与抛物线 交于 两点,当点 的
纵坐标为 1 时, .
(Ⅰ)求抛物线 的方程;
(Ⅱ)若抛物线 上存在点 ,使得 ,求直线 的方程.
21. 已知函数 .
(Ⅰ)若 ,证明:函数 在 上单调递减;
(Ⅱ)是否存在实数 ,使得函数 在 内存在两个极值点?若存在,求实数 的取
值范围;若不存在,请说明理由. (参考数据: , )
( )02: 2 >= ppyxC F l C BA, A
2=AF
C
C 0( 2 )M - y, MBMA ⊥ l
2
ln( ) 1( )R∈x af x = + +a+ ax x
0>a ( )xf [ e )+ ∞,
a ( )xf ( )80, a
693.021 ≈n
3
2e 4.5≈
(二)选考题:共 10 分,请考生在第 22、23 题中任选一题作答. 如果多做,则按所做的第
一题计分.
22. [选修 4—4:坐标系与参数方程]
平面直角坐标系中,已知直线 的参数方程是 ( 为参数),以坐标原点 为极点,
轴的正半轴为极轴,建立极坐标系,曲线 的极坐标方程为 .
(Ⅰ)求直线 的极坐标方程;
(Ⅱ)若直线 与曲线 相交于 两点,求 .
23. [选修 4—5:不等式选讲]
已知函数 .
(Ⅰ)若 ,解不等式 ;
(Ⅱ)若不等式 对任意 恒成立,求实数 的取值范围.
l
=
=
ty
tx
3 t O
x C 03cos82 =+− θpp
l
l C BA, OBOA ⋅
( ) 1−++= xaxxf
0=a ( ) 31 ≤−xf
( ) 12 −≥ axf R∈x a
【参考答案】
一、选择题
1. D 2. A 3. B 4. A 5. C 6. C 7. A 8. D 9. C 10. B 11. D 12. A
二、填空题
13.
14. 15. 16.
三、解答题
17.解:(Ⅰ)
, ,
, , , ,
是等比数列, , 的通项公式为 ,
的前 项和 .
(Ⅱ)由 及 得
,
时, ,
, ,
,
的通项公式为 .,
18.解:(Ⅰ)依题意, ∽N ,故 ;
(Ⅱ)依题意,所求平均数为
3
8
8 5
5
1- ( 1)ey = x+ 10 2
,
( ) n
nn nbababa 23232211 ⋅−+=+++
12311 =−=∴ ba ( ) 72343 2
2211 =⋅−+=+ baba
11 =b 32 =b 11 =∴a 22 =a
{ }na 2
1
2 =
a
a { }na∴ 12 −= n
na
{ }na∴ n 1221
21 −=−
−= n
n
nS
12 −= n
na ( ) n
nn nbababa 23232211 ⋅−+=+++
( ) n
n
n nbbbb 2323222 1
3
2
21 ⋅−+=⋅++++ −
1>n ( ) 1
1
2
3
2
21 2523222 −
−
− ⋅−+=++++ n
n
n nbbbb
( ) ( ) ( ) 111 212252323232 −−− ⋅−=⋅−−−⋅−+=∴ nnn
n
n nnnb 12 −=∴ nbn
11112 b==−× 23122 b==−×
{ }nb∴ 12 −= nbn
X ( )25.03, ( ) 75.025.03 =×=XE
36913445.1575.87551202.065008.055035.045025.035022.025008.0150 =+++++=×+×+×+×+×+×
故所用流量的平均值为 ;
(Ⅲ)由题意可知 ,
,
,
所以, 关于 的回归方程为:
19.(Ⅰ)证明:因为 平面 ,所以
又因为底面 是矩形,所以
又因为 ,所以 平面 .
又因为 平面 ,所以平面 平面 .
(Ⅱ)解:方法一:(几何法)过点 作 ,垂足为点 ,连接 .
不妨设 ,则 .
因为 平面 ,所以 .
又因为底面 是矩形,所以 .
又因为 ,所以 平面 ,所以 A .
又因为 ,所以 平面 ,所以
所以 就是二面角 的平面角.
在 中,由勾股定理得 ,
由等面积法,得 ,
又由平行线分线段成比例定理,得 .
所以 .所以 .
所以 .
M369
35
54321 =++++=x
1105
1601401158550 =++++=y
( )( )
( ) 5.2710
275ˆ
5
1
2
5
1 ==
−
−−
=
∑
∑
=
=
i
i
i
ii
xx
yyxx
b
5.27ˆˆ =−= xbya y x 5.275.27ˆ += xy
⊥PA ABCD CDPA ⊥
ABCD CDAD ⊥
AADPA = ⊥CD PAD
⊂CD PCD ⊥PCD PAD
A PEAM ⊥ M FM
3== ADPA 362 === BCADAB ,
⊥PA ABCD AFPA ⊥
ABCD AFAB ⊥
AABPA = ⊥AF PAB PEAF ⊥
AAFAM = ⊥PE AFM FMPE ⊥
AMF∠ FPEA −−
RtΔPAE 1323 2222 =+=+= AEPAPE
13
136
13
23 =×=⋅=
PE
AEPAAM
3
1==
DC
AE
FD
AF
2
1=
AD
AF
2
3
2
1 == ADAF
4
13
13
136
2
3
tan ===∠
AM
AFAMF
所以二面角 的正切值为 .
方法二:(向量法)以 , , 分别为 , , 轴建立如图所示的空间直角坐标
系:
不妨设 ,则由(Ⅱ)可得 , .
又由平行线分线段成比例定理,得 ,
所以 ,所以 .
所以点 , , .
则 , .
设平面 的法向量为 ,则
由 得 得
令 ,得平面 的一个法向量为 ;
又易知平面 的一个法向量为 ;
设二面角 的大小为 ,则 .
所以 .所以二面角 的正切值为 .
20.解:(Ⅰ) 的准线方程为 ,当点 纵坐标为 1 时 ,
FPEA −−
4
13
AF AB AP x y z
3== ADPA 3=AP 2=AE
3
1==
DC
AE
FD
AF
2
1=
AD
AF
2
3
2
1 == ADAF
( )300 ,,P ( )020 ,,E
002
3 ,,F
( )0 2 -3PE = ,, 3 0 32
PF = −
,,
PEF ( ), ,n x y z=
( ) ( )
( )
0, , 0,2, 3
3 0, , ,0, 32
n PE x y z
n PF x y z
⋅ = ⋅ =− ⋅ = ⋅ =−
,
,
2 3 0
3 3 02
y z
x z
− = − =
,
,
3
2
2
y z
x z
=
=
,
,
1z = PEF 32 12
n = ,,
PEA 3 ,0,02
m AF = =
A PE F− − θ
3 32, ,1 ,0,0 42 2cos
29 3 29
2 2
n m
n m
θ
⋅ ⋅ = = =
×
( )2
2429 13tan 4 4
θ
−
= = A PE F− − 13
4
2: 2C x py=
2
py = − A 2AF =
, , 势物线 的方程为 .
(Ⅱ) 在 上, ,
又 ,设 方程为 ,由 得 ,
令 , ,则 , , , ,
,
, 或 0,
当 时, 过 点(舍), , 方程为 .
21.解:(Ⅰ)函数 的定义域是 .
求导得 .
设 ,则 与 同号.
所以 ,若 ,则 对任意 恒成立.
所以函数 在 上单调递减.
又 ,
所以当 时,满足 .即当 时,满足 .
所以函数 在 上单调递减.
(Ⅱ)①当 时,函数 在 上单调递减.
由 ,又 , 时,
,
取 ,则 ,
所以一定存在某个实数 ,使得 .
故在 上, ;在 上, .
1 22
p∴ + = 2p∴ = ∴ C 2 4x y=
( )
0
2, yM − C
( )2
0
2 14y −∴ = =
( )0,1F l 1y kx= +
2
1
4
y kx
x y
= +
=
, 2 4 4 0x kx− − =
( )
1 1
A x y, ( )
2 2
B x y, 1 2
4x x k+ =
1 2
4x x = − ( )
1 1
2 1MA x y= + − , ( )
2 2
2 1MB x y= + − ,
0MA MB MA MB⊥ ∴ ⋅ =
,
( )( ) ( )( )
1 2 1 2
02 2 1 1x x y y+ =+ + − −
24 8 4 4 0 2k k k∴− + + − = ∴ =,
0k = l M 2k∴ = l∴ 2 1y x= +
( )
2
ln 1x af ax x x
− + + + ( )0 + ∞,
( ) ( ) ( )
2
2 322
1 ln 2 1 2ln1 0
x x x x axxf ax xxxx
⋅ − ⋅ − − ′ = + =− >
( ) 1 2lng x axx = − − ( )f x′ ( )g x
( ) 2g ax x
′ = − − 0a > ( ) 0g x′ < ( )0x ∈ + ∞,
( ) 1 2lng x axx = − − ( )0 + ∞,
( ) 11 2ln e e 1 2 e e 0e 2g a a a= − − = − × − = − <
[ ]ex ∈ + ∞, ( ) ( ) 0eg gx ≤ < [ ]ex ∈ + ∞, ( ) 0f x′ <
( )f x [ ]e + ∞,
0a ≥ ( ) 1 2lng x axx = − − ( )0 + ∞,
( ) 1 2ln e e e 0eg a a= − − = − ≤ 0a ≥ 0 ex< ≤
( ) 1 2ln 1 2ln 2g x ax x ax = − − ≥ − −
1
2e ax −= ( )1
2
11 2 2 0e 2
ag aa−
≥ − − =−
(0
0 ex ∈ , ( )
0
0g x =
( )
0
0x x∈ , ( ) 0g x > ( )
0
x x∈ + ∞, ( ) 0g x <
即在 上, ;在 上, .
所以函数 在 上单调递增,在 上单调递减.此时函数 只有 1 个极值点
,不合题意,舍去;
②当 时,令 ,得 ;令 ,得 ,
所以函数 在 上单调递减,在 上单调递增.
故函数 的单调情况如下表:
0 +
极小值
要使函数 在 内存在两个极值点,则需满足 即 ,
解得 又 , ,
所以 . 此时, ,
又 , ;
综上,存在实数 ,使得函数 在 内存在两个极值点.
22.解:(Ⅰ)由 得 ,
的极坐标方程为 即 , .
( )
0
0x x∈ , ( ) 0f x′ > ( )
0
x x∈ + ∞, ( ) 0f x′ <
( )f x ( )
0
0 x, ( )
0
x + ∞, ( )f x
0
x
0a < ( ) 2 0g ax x
′ = − − > 2x a
> − ( ) 2 0g ax x
′ = − − < 20 x a
< < −
( )g x 20 a
− , 2
a
− + ∞ ,
( )g x
x 20 a
− , 2
a
− 2
a
− + ∞ ,
( )g x′ −
( )g x
( )f x ( )0 8, ( )
2 0
08
20 8
g
a
g
a
<− >
< − <
,
,
,
2 21 2ln 0
1 2ln8 8 0
20 8
a
a a
a
a
− − <− − − − >
< − <
,
,
,
3
2
2
1 3 ln28 4
1
4.
a
e
a
a
> −
< −
< −
,
, 3
2
2 2 0.444.5e
− ≈ − ≈ − 1 3 1 3ln2 0.693 0.3958 4 8 4
− ≈ − × ≈ −
3
2
2 1 3 ln28 4e
a− < < − 2 e e
2 ea
− > >
e e e1e 1 2 2 2 0e e e2e
g a a a
= − × − ⋅ = − ⋅ = − ⋅ >− 3
2
2 1 3 ln28 4e
a
− −∴ ∈
,
3
2
2 1 3 ln28 4e
a
− −∈
, ( )f x ( )0 8,
3
x t
y t
= =
,
3y x=
l∴ sin 3 cosρ θ ρ θ= 3θ = ( )π
3 Rθ ρ= ∈
(Ⅱ)由 得 ,
设 , ,则 , .
23.解:(Ⅰ) 时, ,
由 得 ,
不等式 的解集为 .
(Ⅱ) 对 成立,
又 对 成立, ,
, 即 .
2
π
3
8 cos 3 0
θ
ρ ρ θ
=
− + =
, 2 4 3 0ρ ρ− + =
( )
1 1
,A ρ θ ( )
2 2
,B ρ θ
1 2
3ρ ρ =
1 2
3OA OB ρ ρ∴ ⋅ = =
0a = ( ) 1f x x x= + − ( )
2 3 2
1 1 21 1 2
2 3 1
x x
f xx x x
x x
− >
= + = ≤ ≤− − −
− + <
, ,
, ,
, ,
( ) 31f x ≤− 0 3x≤ ≤
∴ ( ) 31f x ≤− [ ]0 3,
( ) ( ) ( ) 11f x ax a x≥ =− ++ − Rx ∈
( ) 2 1f x a≥ − Rx ∈ 1 2 1a a∴ ≥+ −
2 22 1 4 4 1a a a a∴ + + ≥ − + 0 2a∴ ≤ ≤ [ ]0 2a ∈ ,