- 2021-04-12 发布 |
- 37.5 KB |
- 8页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2017届四川省成都七中高三一诊模拟考试(2016
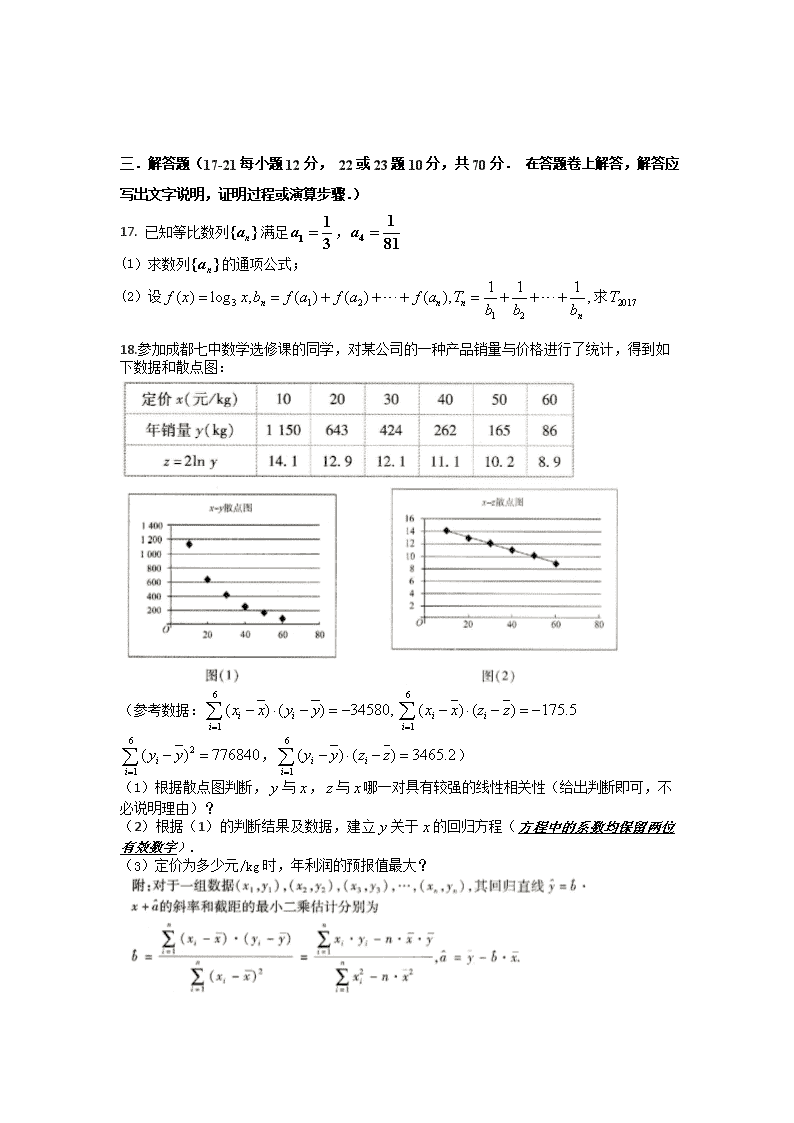
成都七中2017届一诊模拟考试数学试卷(理科) 考试时间:120分钟 总分:150分 命题人:刘在廷 审题人:张世永 一.选择题(每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求.把答案凃在答题卷上.) 1.设全集为,集合,则( ) A B C D 2.设为虚数单位,复数的虚部为( ) A B 1 C D 3. 已知点不在同一条直线上,点为该平面上一点,且,则( ) A.点不在直线上 B.点在线段上 C.点在线段的延长线上 D.点在线段的反向延长线上 4.我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( ) A 44,45,56 B 44,43,57 C 44,43,56 D 45,43,57 5. 在三角形ABC中,,则( ) A 或 B C D 以上都不对 6. 如图所示的程序框图输出的S是126,则条件①可以为( ) A n≤5 B n≤6 C n≤7 D n≤8 7. 住在狗熊岭的7只动物,它们分别是熊大,熊二,吉吉,毛毛,蹦蹦,萝卜头,图图。为了更好的保护森林,它们要选出2只动物作为组长,则熊大,熊二至少一个被选为组长的概率为( ) A B C D 8.某三棱锥的三视图如图所示,则该三棱锥的表面积是( ) A B 5 C D 9. 如果实数满足关系又 恒成立,则的取值范围为( ) A B C D 10. 已知函数,若在区间内,曲线与轴有三个不同的交点,则实数的取值范围是 ( ) A B C D 11. 函数的最小值为,函数的最小正周期为,则的值为( ) A B C D 12. 已知椭圆,其左、右焦点分别为,关于椭圆有以下四种说法:(1)设A为椭圆上任一点,其到直线的距离分别为,则;(2)设A为椭圆上任一点,分别与椭圆交于两点,则(当且仅当点A在椭圆的顶点取等);(3)设A为椭圆上且不在坐标轴上的任一点,过A的椭圆切线为,为线段上一点,且,则直线;(4)面积为的椭圆内接四边形仅有1个。 其中正确的有( )个. A 1 B 2 C 3 D 4 二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。) 13. 若,则的展开式中的常数项为________(用数字作答) 14.已知非直角△ABC中,内角A,B,C的对边分别是,其中,又,若,则△ABC的面积为_________. 15. 具有公共轴的两个直角坐标平面和所成的二面角等于,已知内的曲线的方程是,曲线在内的射影在平面内的曲线方程为,则_____________. 16.已知,且满足的整数共有个,的最小值为,且,则实数的值为___________. 三.解答题(17-21每小题12分, 22或23题10分,共70分. 在答题卷上解答,解答应写出文字说明,证明过程或演算步骤.) 17. 已知等比数列满足, (1)求数列的通项公式; (2)设求 18.参加成都七中数学选修课的同学,对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图: (参考数据: ,) (1)根据散点图判断,与,与哪一对具有较强的线性相关性(给出判断即可,不必说明理由)? (2)根据(1)的判断结果及数据,建立关于的回归方程(方程中的系数均保留两位有效数字). (3)定价为多少元/kg时,年利润的预报值最大? 19. 如图,直角三角形中,点在斜边上,且是平面同一侧的两点,平面平面 ⑴ 求证:平面平面 ⑵ 点在线段上,且二面角的余弦值为,求的长度。 20.平面上两定点,,动点满足 (1)求动点的轨迹; (2)当时,动点的轨迹为曲线,已知,过的动直线(斜率存在 且不为0)与曲线交于P,Q两点,,直线,SP,SQ分别与交于A,B两 点.A,B,P,Q坐标分别为,,, 求证:为定值,并求出此定值; 21.已知,其中(与关于直线对称) (1)若函数在区间上递增,求的取值范围; (2)证明:; (3)设,其中恒成立,求满足条件的最小整数的值。 请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分. 选修4-4:坐标系与参数方程 22.已知直线的参数方程为为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为. (1) 求圆的直角坐标方程; (2) 若是直线与圆面的公共点,求的取值范围. 选修4-5:不等式选讲 23.已知函数 ⑴ 当时,求不等式的解集; ⑵ 若时,恒成立,求的最小值. 成都七中2017届一诊模拟考试数学试卷(理科)(参考答案) 一.选择题 1-5:BADBC 6-10:BCDCA 11-12:BA 二、填空题 13. 1120; 14. ; 15.4 16. 0或-2 三.解答题 17. 解:(1)∵为等比数列,设公比为 又 即数列是首项为公比为的等比数列 (2)由已知可得: 则: 故: 19. 证明:(Ⅰ)∵直角三角形ABC中,∠BAC=60°,AC=4, ∴AB=8,AF=AB=2,由余弦定理得CF=2且CF⊥AB. ∵AD⊥平面ABC,CF⊂平面ABC, ∴AD⊥CF,又AD∩AB=A,∴CF⊥平面DABE, ∴CF⊥DF,CF⊥EF. ∴∠DFE为二面角D﹣CF﹣E的平面角. 又AF=2,AD=3,BE=4,BF=6, 故Rt△ADF∽Rt△BFE.∴∠ADF=∠BFE,∴∠AFD+∠BFE=∠AFD+∠ADF=90°, ∴∠DFE=90°,D﹣CF﹣E为直二面角.∴平面CDF⊥平面CEF. (建系求解,只要答案正确,也给分) (2)以C为坐标原点,建立如图所示的空间直角坐标系C﹣xyz,设 ∴ 则面DMF的法向量: 同理可知:面CDM的法向量 由,则 或 经检验,时二面角的余弦值为 不合题意 所以 20. 解:(1)由题意:当时,动点不表示任何图形; 当时,动点的轨迹是线段; 当时,动点的轨迹是椭圆 (2)当时,动点的轨迹方程为: 设,则 可得: ∴ ∴ ∴ 又点在直线上, ∴ ∴ 同理: 又 由 则,则 同理: ∴ ∴ 21. 解:(1)由题意:恒成立, 则恒成立。又单调递减, ∴ (2)由(1)知,当时,在单调增 ∴ ∴ ∴ ∴ (3)由 即: 又 ∵ 则 ∴单调增,又 则必然存在,使得 ∴在单减,单增, ∴ 则,又 ∴ ∴ 又则 ∴,恒成立 令, 则 ∴在单调递增 又 ∴ ∴在单调递增 ∴ ∴ 又为整数 ∴最小整数的值为:2 请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一题计分. 22.解:(1)∵圆的极坐标方程为.∴, 又∵,,.∴, ∴圆的普通方程为; (2)设.由(1)知圆的方程, ∴圆的圆心是,半径是.将代入得, 又∵直线过,圆的半径是.∴. ∴,即的取值范围是. 23.解:(Ⅰ)当m=2时,, 作出图象(右边): 结合图象由的单调性及得的解集为 (2)由得 ∵∴ 在同一直角坐标系中画出及的图象, 根据图象性质可得即 故的最小值为查看更多