人教版高三数学总复习课时作业47

人教版高三数学总复习课时作业47

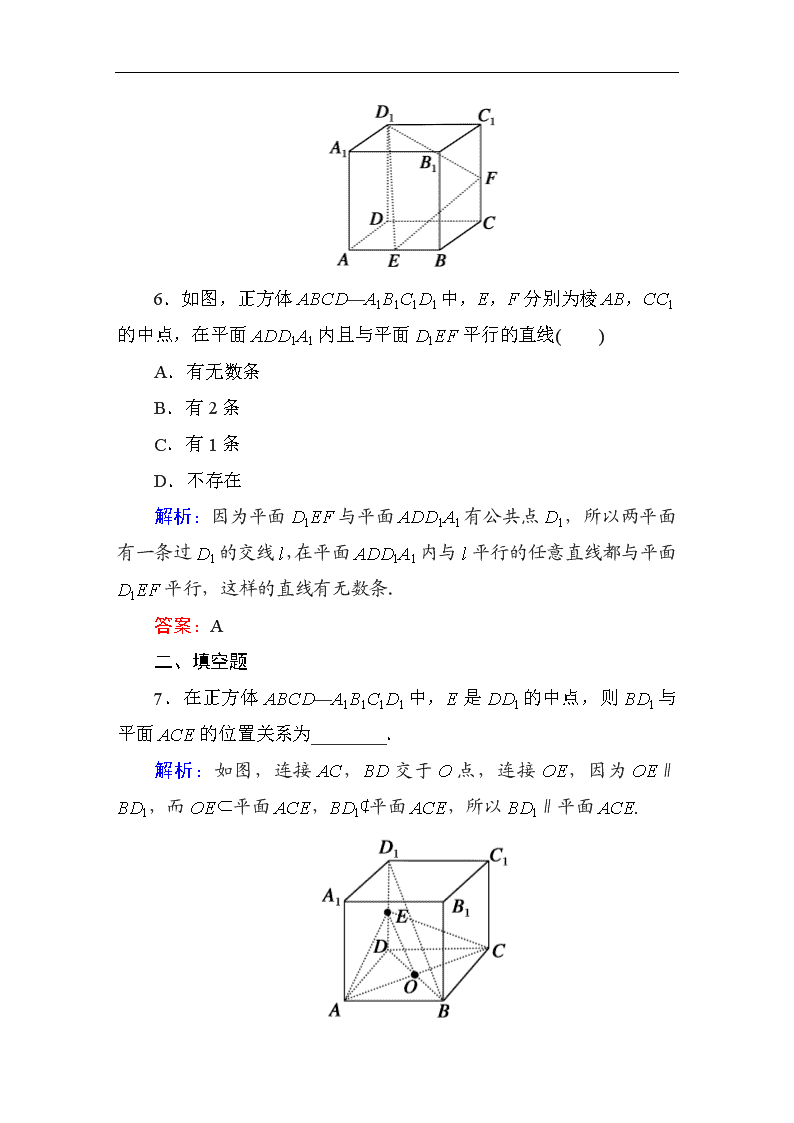
课时作业47　直线、平面平行的判定及其性质 一、选择题 ‎1．平面α∥平面β，点A，C∈α，点B，D∈β，则直线AC∥直线BD的充要条件是(　　)‎ A．AB∥CD B．AD∥CB C．AB与CD相交 D．A，B，C，D四点共面 解析：充分性：A，B，C，D四点共面，由平面与平面平行的性质知AC∥BD.必要性显然成立．‎ 答案：D ‎2．一条直线l上有相异三个点A、B、C到平面α的距离相等，那么直线l与平面α的位置关系是(　　)‎ A．l∥α B．l⊥α C．l与α相交但不垂直 D．l∥α或l⊂α 解析：l∥α时，直线l上任意点到α的距离都相等；l⊂α时，直线l上所有的点到α的距离都是0；l⊥α时，直线l上有两个点到α距离相等；l与α斜交时，也只能有两个点到α距离相等．故选D.‎ 答案：D ‎3．已知不重合的两条直线l，m和不重合的两个平面α，β，下列命题正确的是(　　)‎ A．l∥m，l∥β，则m∥β B．α∩β＝m，l⊂α，则l∥β C．α⊥β，l⊥α，则l∥β D．l⊥m，m⊥β，l⊥α，则α⊥β 解析：对于选项A，m可能在β内，故A错；对于选项B，l可能与β相交，故B错；对于选项C，l可能在β内，故C错，所以选D.‎ 答案：D ‎4．已知l、m是两条不同的直线，α是一个平面，则下列命题正确的是(　　)‎ A．若l∥α，m∥α，则l∥m B．若l⊥m，m∥α，则l⊥α C．若l⊥m，m⊥α，则l∥α D．若l∥α，m⊥α，则l⊥m 解析：A选项，l与m可能平行，异面或相交，A错；B选项，l与α可能平行，相交或l在α内，B错；C选项，l有可能在α内，C错，故选D.‎ 答案：D ‎5．已知α，β是两个不同的平面，m，n是两条不同的直线，给出下列命题：‎ ‎①若m⊥α，m⊂β，则α⊥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③如果m⊂α，n⊄α，m，n是异面直线，那么n与α相交；④若α∩β＝m，n∥m，且n⊄α，n⊄β，则n∥α且n∥β.‎ 其中正确的命题是(　　)‎ A．①② B．②③‎ C．③④ D．①④‎ 解析：由面面垂直的判定定理得①正确，若m∥n时，α，β有可能相交，所以②错误．对③来说，n可能与α平行，则③错．α∩β＝m，∴m⊂α，m⊂β，n⊄α，n∥m，则n∥α，同理n∥β，选D.‎ 答案：D ‎6．如图，正方体ABCD—A1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线(　　)‎ A．有无数条 B．有2条 C．有1条 D．不存在 解析：因为平面D1EF与平面ADD1A1有公共点D1，所以两平面有一条过D1的交线l，在平面ADD1A1内与l平行的任意直线都与平面D1EF平行，这样的直线有无数条．‎ 答案：A 二、填空题 ‎7．在正方体ABCD—A1B1C1D1中，E是DD1的中点，则BD1与平面ACE的位置关系为________．‎ 解析：如图，连接AC，BD交于O点，连接OE，因为OE∥BD1，而OE⊂平面ACE，BD1⊄平面ACE，所以BD1∥平面ACE.‎ 答案：平行 ‎8．α、β、γ是三个平面，a、b是两条直线，有下列三个条件：①a∥γ，b⊂β；②a∥γ，b∥β；③b∥β，a⊂γ.如果命题“α∩β＝a，b⊂γ，且________，则a∥b”为真命题，则可以在横线处填入的条件是________(把所有正确的题号填上)．‎ 解析：①中，a∥γ，a⊂β，b⊂β，β∩γ＝b⇒a∥b(线面平行的性质)．③中，b∥β，b⊂γ，a⊂γ，β∩γ＝a⇒a∥b(线面平行的性质)．‎ 答案：①③‎ ‎9．在正四棱柱ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则点Q满足条件________时，有平面D1BQ∥平面PAO.‎ 解析：假设Q为CC1的中点，因为P为DD1的中点，所以QB∥PA.连接DB，因为P，O分别是DD1，DB的中点，所以D1B∥PO，又D1B⊄平面PAO，QB⊄平面PAO，所以D1B∥平面PAO，QB∥平面PAO，又D1B∩QB＝B，所以平面D1BQ∥平面PAO.故Q满足条件Q为CC1的中点时，有平面D1BQ∥平面PAO.‎ 答案：Q为CC1的中点 三、解答题 ‎10．如图，已知四棱锥P—ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC＝AB＝1，M是PB 的中点．‎ ‎(1)求证：AM＝CM；‎ ‎(2)若N是PC的中点，求证：DN∥平面AMC.‎ 证明：(1)∵在直角梯形ABCD中，AD＝DC＝AB＝1，‎ ‎∴AC＝，BC＝，‎ ‎∴BC⊥AC，又PA⊥平面ABCD，BC⊂平面ABCD，‎ ‎∴BC⊥PA，又PA∩AC＝A，∴BC⊥平面PAC，‎ ‎∴BC⊥PC.‎ 在Rt△PAB中，M为PB的中点，则AM＝PB，‎ 在Rt△PBC中，M为PB的中点，则CM＝PB，‎ ‎∴AM＝CM.‎ ‎(2)如图，连接DB交AC于点F，‎ ‎∵DC綊AB，∴DF＝FB.‎ 取PM的中点G，连接DG，FM，则DG∥FM，‎ ‎∴又DG⊄平面AMC，FM⊂平面AMC，‎ ‎∴DG∥平面AMC.‎ 连接GN，则GN∥MC，GN⊄平面AMC，MC⊂平面AMC.‎ ‎∴GN∥平面AMC，又GN∩DG＝G，‎ ‎∴平面DNG∥平面AMC，‎ 又DN⊂平面DNG，‎ ‎∴DN∥平面AMC.‎ ‎11．如右图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF＝3，G和H分别是CE和CF的中点．‎ ‎(1)求证：AC⊥平面BDEF；‎ ‎(2)求证：平面BDGH∥平面AEF.‎ 解：(1)因为四边形ABCD是正方形，所以AC⊥BD.‎ 又因为平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD＝BD，且AC⊂平面ABCD，所以AC⊥平面BDEF.‎ ‎(2)在△CEF中，因为G，H分别是CE，CF的中点，所以GH∥EF，‎ 又因为GH⊄平面AEF，EF⊂平面AEF，所以GH∥平面AEF.‎ 设AC∩BD＝O，连接OH，‎ 在△ACF中，因为OA＝OC，CH＝HF，所以OH∥AF，‎ 又因为OH⊄平面AEF，AF⊂平面AEF，所以OH∥平面AEF.‎ 又因为OH∩GH＝H，OH，GH⊂平面BDGH，‎ 所以平面BDGH∥平面AEF.‎ ‎1．下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是(　　)‎ A．①③ B．②③‎ C．①④ D．②④‎ 解析：对于图形①：平面MNP与AB所在的对角面平行，即可得到AB∥平面MNP，对于图形④：AB∥PN，即可得到AB∥平面MNP，图形②，③都不可以，故选C.‎ 答案：C ‎2．如图，在长方体ABCD—A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足条件________时，有MN∥平面B1BDD1.‎ 解析：‎ 如图，连接FH，HN，FN，‎ 由题意知HN∥面B1BDD1，FH∥面B1BDD1.‎ 且HN∩FH＝H，‎ ‎∴面NHF∥面B1BDD1.‎ ‎∴当M在线段HF上运动时，有MN∥面B1BDD1.‎ 答案：M∈线段HF ‎3．如图1，已知⊙O的直径AB＝4，点C、D为⊙O上两点，且∠CAB＝45°，∠DAB＝60°，F为弧BC的中点，将⊙O沿直径AB折起，使两个半圆所在平面互相垂直(如图2)．‎ ‎(1)求证：OF∥AC；‎ ‎(2)在弧BD上是否存在点G，使得FG∥平面ACD？若存在，试指出点G的位置；若不存在，请说明理由．‎ 解：‎ 解法1：(1)证明：如右图，连接CO，‎ ‎∵∠CAB＝45°，∴CO⊥AB，‎ 又∵F为弧BC的中点，∴∠FOB＝45°，∴OF∥AC.‎ ‎(2)取弧BD的中点G，连接OG，FG，‎ 则∠BOG＝∠BAD＝60°，故OG∥AD 由(1)OF∥AC，知OF∥平面ACD，故平面OFG∥平面ACD，则FG∥平面ACD，因此，在弧BD上存在点G，使得FG∥平面ACD，且点G为弧BD的中点．‎ 解法2：证明：(1)如下图，以AB所在的直线为y轴，以OC所在的直线为z轴，以O为原点，作空间直角坐标系O—xyz，则A(0，－2，0)，C(0,0,2)‎ ＝(0,0,2)－(0，－2,0)＝(0,2,2)，‎ ‎∵点F为弧BC的中点，∴点F的坐标为(0，，)，‎ ＝(0，，)，‎ ‎∴＝，即OF∥AC.‎ ‎(2)设在弧BD上存在点G，使得FG∥平面ACD，‎ 由(1)OF∥AC，知OF∥平面ACD，∴平面OFG∥平面ACD，则有OG∥AD.‎ 设＝λ(λ>0)，∵＝(，1,0)，∴＝(3λ，λ，0)．又∵||＝2，∴＝2，解得λ＝±1(舍去－1)，∴＝(，1,0)，则G为弧BD的中点．‎ 因此，在弧BD上存在点G，使得FG∥平面ACD，且点G为弧BD的中点．‎