- 2021-04-12 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教版(理)第2章第7讲函数的图象学案
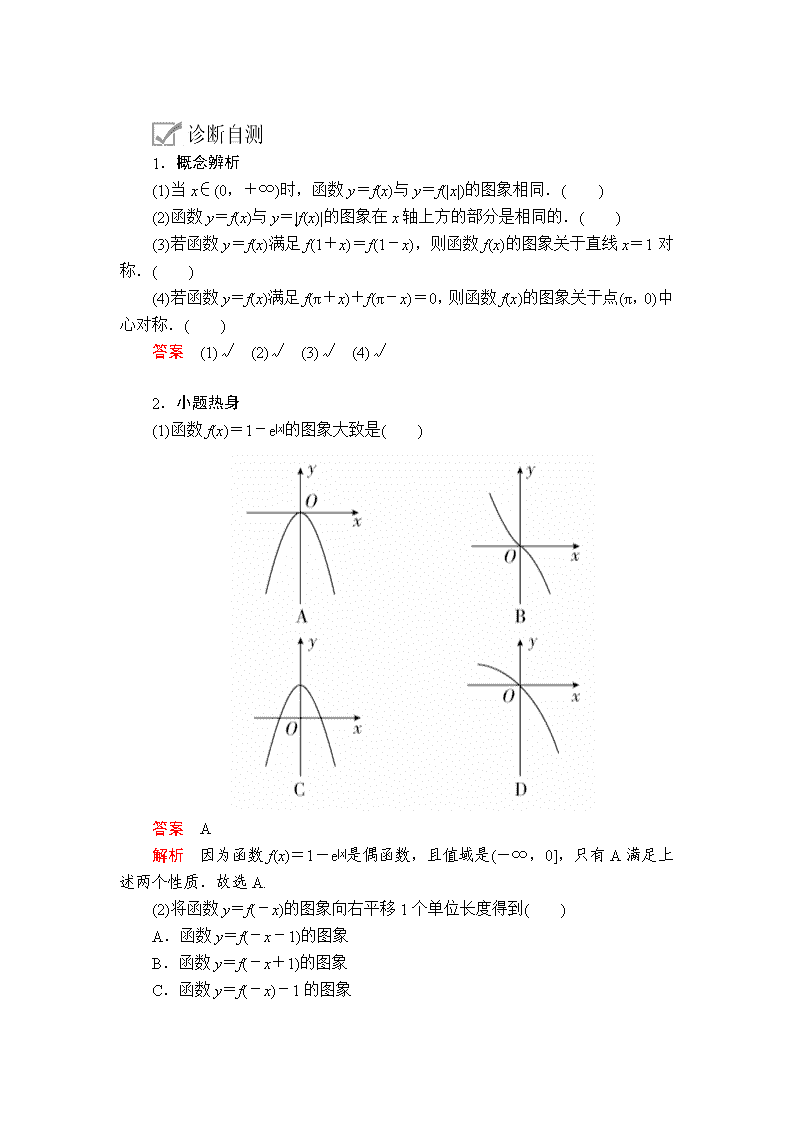
第7讲 函数的图象 [考纲解读] 1.掌握基本初等函数的图象特征,能熟练地运用基本初等函数的图象解决问题. 2.掌握作函数图象的常用方法:①描点法;②平移法;③对称法.(重点) 3.能运用函数图象理解和研究函数的性质、解决方程解的个数或与不等式相关的问题.(难点) [考向预测] 从近三年高考情况来看,本讲一直是高考中的热点.预测2020年高考将会考查:①已知函数解析式识别函数的图象;②利用函数图象求函数零点的个数、解不等式或求参数的取值范围.题型以客观题为主,在解答题中也会用到数形结合的思想进行求解. 1.利用描点法作函数图象的流程 2.变换法作图 (1)平移变换 提醒:对于平移,往往容易出错,在实际判断中可熟记口诀:左加右减,上加下减. (2)对称变换 ①y=f(x)y=-f(x); ②y=f(x)y=f(-x); ③y=f(x)y=-f(-x); ④y=ax(a>0且a≠1)y=logax(a>0且a≠1). (3)翻折变换 ①y=f(x)y=|f(x)|; ②y=f(x)y=f(|x|). (4)伸缩变换 1.概念辨析 (1)当x∈(0,+∞)时,函数y=f(x)与y=f(|x|)的图象相同.( ) (2)函数y=f(x)与y=|f(x)|的图象在x轴上方的部分是相同的.( ) (3)若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线x=1对称.( ) (4)若函数y=f(x)满足f(π+x)+f(π-x)=0,则函数f(x)的图象关于点(π,0)中心对称.( ) 答案 (1)√ (2)√ (3)√ (4)√ 2.小题热身 (1)函数f(x)=1-e|x|的图象大致是( ) 答案 A 解析 因为函数f(x)=1-e|x|是偶函数,且值域是(-∞,0],只有A满足上述两个性质.故选A. (2)将函数y=f(-x)的图象向右平移1个单位长度得到( ) A.函数y=f(-x-1)的图象 B.函数y=f(-x+1)的图象 C.函数y=f(-x)-1的图象 D.函数y=f(-x)+1的图象 答案 B 解析 函数y=f(-x)的图象向右平移1个单位长度,得到函数y=f(-(x-1)),即y=f(-x+1)的图象. (3)已知函数f(x)的图象如图所示,则函数g(x)=logf(x)的定义域是________. 答案 (2,8] 解析 结合图象知不等式f(x)>0的解集为(2,8],所以函数g(x)=log f(x)的定义域是(2,8]. (4)如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是________. 答案 (-1,1] 解析 作出函数y=log2(x+1)的图象,如图所示: 其中函数f(x)与y=log2(x+1)的图象的交点为D(1,1),由图象可知 f(x)≥log2(x+1)的解集为{x|-1查看更多