- 2021-04-12 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考卷 05高考文科数学(浙江卷)试题及答案
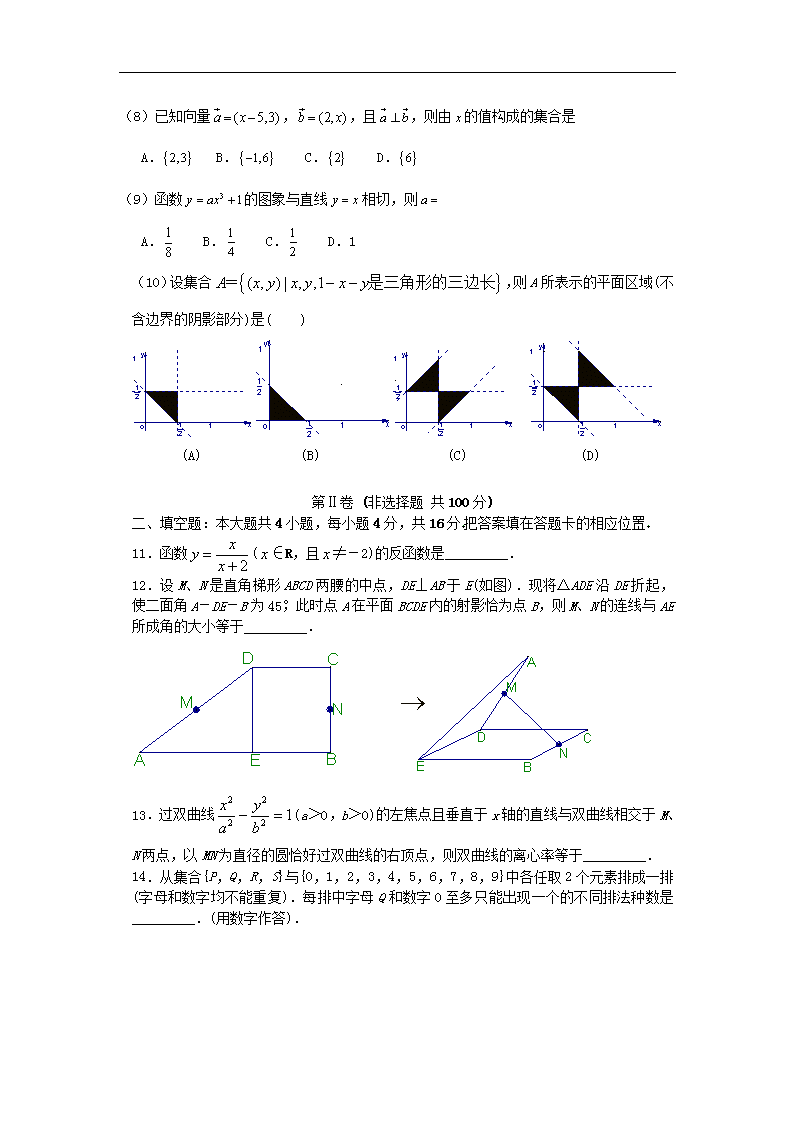
2005年高考文科数学浙江卷试题及答案 第Ⅰ卷 (选择题 共60分) 一、选择题:本大题共10小题,每小题5分,共50分在每小题给出的四个选项中,只有一项是符合题目要求的 (1)函数的最小正周期是 A. B. C. D. (2)设全集,,,则= A. B. C. D. (3)点(1,-1)到直线的距离是( ) (A) (B) (C) (D) (4)设,则( ) (A) (B)0 (C) (D) 1 (5)在的展开式中,含的项的系数是( ) (A) (B) 5 (C) -10 (D) 10 (6)从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码统计结果如下: 卡片号码 1 2 3 4 5 6 7 8 9 10 取到的次数 13 8 5 7 6 13 18 10 11 9 则取到号码为奇数的频率是 A. B. C. D. (7)设、 为两个不同的平面,、为两条不同的直线,且,,有如下的两个命题:①若∥,则∥;②若⊥,则⊥. 那么 (A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题 (C) ①②都是真命题 (D) ①②都是假命题 (8)已知向量,,且,则由的值构成的集合是 A. B. C. D. (9)函数的图象与直线相切,则 A. B. C. D.1 (10)设集合,则A所表示的平面区域(不含边界的阴影部分)是( ) (A) (B) (C) (D) 第Ⅱ卷 (非选择题 共100分) 二、填空题:本大题共4小题,每小题4分,共16分把答案填在答题卡的相应位置 11.函数(∈R,且≠-2)的反函数是_________. 12.设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________. 13.过双曲线(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________. 14.从集合{P,Q,R,S}与{0,1,2,3,4,5,6,7,8,9}中各任取2个元素排成一排(字母和数字均不能重复).每排中字母Q和数字0至多只能出现一个的不同排法种数是_________.(用数字作答). 三、解答题:本大题共6小题,每小题14分,共84分解答应写出文字说明,证明过程或演算步骤 15.已知函数 (Ⅰ) 求的值; (Ⅱ) 设∈(0,),,求sin的值. 16.已知实数成等差数列,成等比数列,且,求 17.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是,从B中摸出一个红球的概率为p. (Ⅰ) 从A中有放回地摸球,每次摸出一个,共摸5次求 (i)恰好有3摸到红球的概率;(ii)第一次、第三次、第五次均摸到红球的概率. (Ⅱ) 若A、B两个袋子中的球数之比为,将A、B中的球装在一起后,从中摸出一个红球的概率是,求p的值. 18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA,点O、D分别是AC、PC的中点,OP⊥底面ABC. (Ⅰ)求证∥平面 (Ⅱ) 求直线与平面PBC所成角的大小; 19.如图,已知椭圆的中心在坐标原点,焦点在x轴上,长轴A1A2的长为4,左准线与x轴的交点为M,|MA1|∶|A1F1|=2∶1. (Ⅰ)求椭圆的方程; (Ⅱ)若点P在直线上运动,求∠F1PF2的最大值. 20.函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x. (Ⅰ)求函数g(x)的解析式; (Ⅱ)解不等式g(x)≥f(x)-|x-1|. (Ⅲ)若在上是增函数,求实数的取值范围 2005年高考文科数学浙江卷试题及答案 参考答案 一、选择题:本题考查基本知识和基本运算每小题5分,满分50分 (1)B (2)A (3)D (4)D (5)C (6)A (7)D (8)C (9)B (10)A 二、填空题:本题考查基本知识和基本运算每小题4分,满分16分 (11);(12);(13)2;(14)5832 三、解答题: (15)本题主要考查三角函数的倍角公式、两角和的公式等基础知识和基本的运算能力满分14分 解:(Ⅰ)∵ ∴ (Ⅱ) ∴ ∵, ∴, 故 (16)本题主要考查等差、等比数列的基本知识考查运算及推理能力满分14分 解:由题意,得 由(1)(2)两式,解得 将代入(3),整理得 (17)本题主要考查排列组合、相互独立事件同时发生的概率等基本知识,同时考查学生的逻辑思维能力满分14分 解:(Ⅰ)(ⅰ) (ⅱ). (Ⅱ)设袋子A中有个球,袋子B中有个球, 由,得 (18)本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力满分14分 解:方法一: (Ⅰ) ∵O、D分别为AC、PC中点, (Ⅱ) 方法二: (19)本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识,考查解析几何的基本思想方法和综合解题能力满分14分 解:(Ⅰ)设椭圆方程为,半焦距为,则 (Ⅱ) (20)本题主要考查函数图象的对称、二次函数的基本性质与不等式的应用等基础知识,以及综合运用所学知识分析和解决问题的能力满分14分 解:(Ⅰ)设函数的图象上任意一点关于原点的对称点为,则 ∵点在函数的图象上 ∴ (Ⅱ)由 当时,,此时不等式无解 当时,,解得 因此,原不等式的解集为 (Ⅲ) ① ② ⅰ) ⅱ)查看更多