【数学】2019届一轮复习人教A版(文)第三章第4节函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用学案
第四节函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
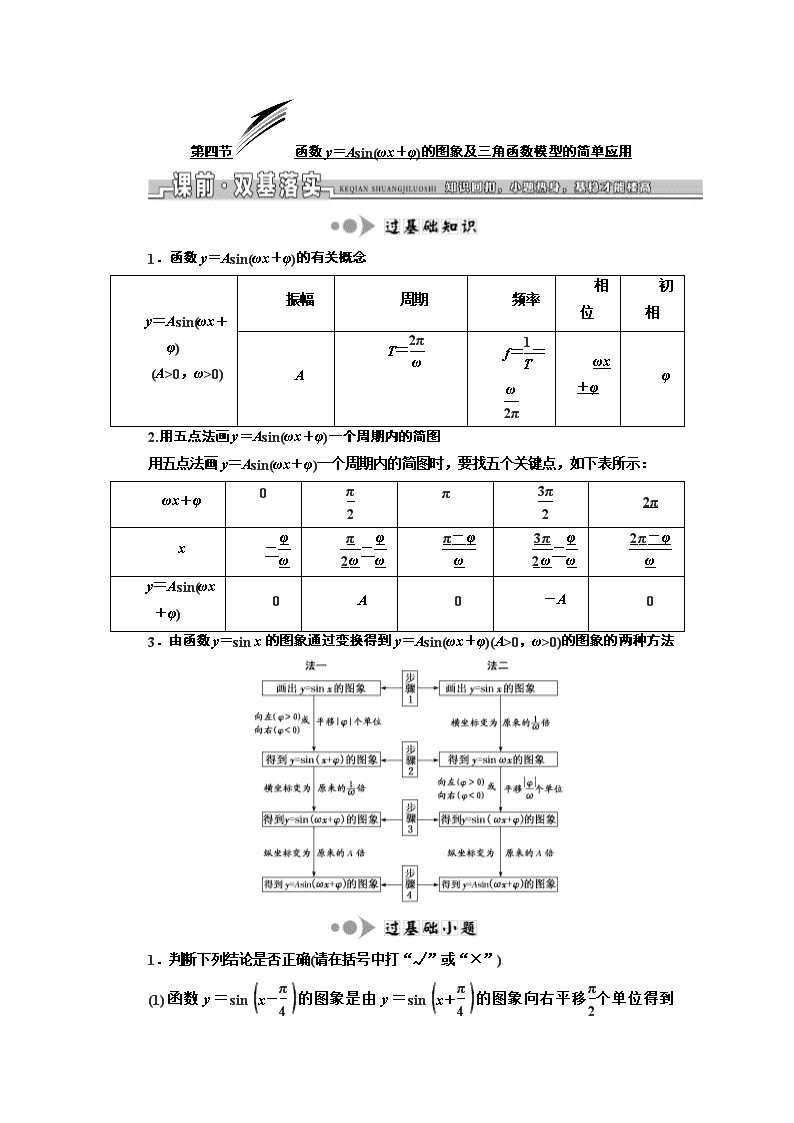
1.函数y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ)
(A>0,ω>0)
振幅
周期
频率
相位
初相
A
T=
f==
ωx+φ
φ
2.用五点法画y=Asin(ωx+φ)一个周期内的简图
用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示:
ωx+φ
2π
x
-
-
-
y=Asin(ωx+φ)
0
A
0
-A
0
3.由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)函数y=sin的图象是由y=sin的图象向右平移个单位得到的.( )
(2)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( )
(3)函数y=Asin(ωx+φ)的最小正周期为T=.( )
(4)把函数y=sin x的图象上各点纵坐标不变,横坐标缩短为原来的,所得图象对应的函数解析式为y=sinx.( )
答案:(1)√ (2)× (3)× (4)×
2.函数y=2sin的振幅、频率和初相分别为( )
A.2,, B.2,,
C.2,, D.2,,-
解析:选A 由振幅、频率和初相的定义可知,函数y=2sin的振幅为2,频率为,初相为.
3.函数y=cos x|tan x|的图象为( )
解析:选C 由题意知y=
结合图象知选C.
4.为了得到函数y=2sin的图象,可以将函数y=2sin 2x的图象( )
A.向右平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向左平移个单位长度
解析:选A 函数y=2sin=2sin,可由函数y=2sin 2x的图象向右平移
eq f(π,6)个单位长度得到.故选A.
5.用五点法作函数y=sin在一个周期内的图象时,主要确定的五个点是______、______、______、______、______.
答案:
6.函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则f的值为________.
解析:由图象可知A=2,T=-=,∴T=π,∴ω=2,
∵当x=时,函数f(x)取得最大值,
∴2×+φ=+2kπ(k∈Z),∴φ=+2kπ(k∈Z),
∵0<φ<π,∴φ=,∴f(x)=2sin,
则f=2sin=2cos=.
答案:
三角函数图象的变换多出现在选择题中,以y=sin x,y=cos x,y=tan x的图象为基础,进行横向伸缩变换及纵向伸缩变换,或者由正弦型、余弦型、正切型函数图象为基础进行逆向变换.属于必得分题.
[典题领悟]
(2017·全国卷Ⅰ)已知曲线C1:y=cos x,C2:y=sin,则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
解析:选D 易知C1:y=cos x=sin,把曲线C1上的各点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=sin的图象,再把所得函数的图象向左平移个单位长度,可得函数y=sin=sin的图象,即曲线C2.
[解题师说]
1.掌握三角函数的图象变换的2方法
(1)平移变换
沿x轴平移
由y=f(x)变为y=f(x+φ)时,“左加右减”,即φ>0,左移;φ<0,右移
沿y轴平移
由y=f(x)变为y=f(x)+k时,“上加下减”,即k>0,上移;k<0,下移
(2)伸缩变换
沿x轴伸缩
由y=f(x)变为y=f(ωx)时,点的纵坐标不变,横坐标变为原来的倍
沿y轴伸缩
由y=f(x)变为y=Af(x)时,点的横坐标不变,纵坐标变为原来的|A|倍
2.注意三角函数图象变换中的3问题
(1)变换前后,函数的名称要一致,若不一致,应先利用诱导公式转化为同名函数;
(2)要弄清变换的方向,即变换的是哪个函数的图象,得到的是哪个函数的图象,切不可弄错方向;
(3)要弄准变换量的大小,特别是平移变换中,函数y=Asin x到y=Asin(x+φ)的变换量是|φ|个单位,而函数y=Asin ωx到y=Asin(ωx+φ)时,变换量是个单位.
[冲关演练]
1.(2016·全国卷Ⅰ)将函数y=2sin的图象向右平移个周期后,所得图象对应的函数为( )
A.y=2sin B.y=2sin
C.y=2sin D.y=2sin
解析:选D 函数y=2sin的周期为π,将函数y=2sin的图象向右平移个周期即个单位长度,所得图象对应的函数为y=2sin=2sin,故选D.
2.(2018·昆明质检)已知函数f(x)=sin(0<ω<2)满足条件:f=0,为了得到函数y=f(x)的图象,可将函数g(x)=cos ωx的图象向右平移m(m>0)个单位长度,则m的最小值为( )
A.1 B.
C. D.
解析:选A 由题意,得sin=0,即-ω+=kπ(k∈Z),则ω=-2kπ(k∈Z),结合0<ω<2,得ω=,所以f(x)=sin=cos=cos,所以只需将函数g(x)=cosx的图象向右至少平移1个单位长度,即可得到函数y=f(x)的图象,故选A.
根据三角函数的图象(或性质)求解析式是高考对三角函数知识考查的一个重要方面,主要考查由图象(或性质)求解析式;由图象(或性质)求解析式中参数的值;由图象(或性质)解决相关的求值问题等.多以选择题、填空题的形式出现,有时也可能在解答题中出现,难度为中低档题.
[典题领悟]
1.函数f(x)=Asin(ωx+φ)A>0,ω>0,|φ|<的部分图象如图所示,则f的值为( )
A.- B.-
C.- D.-1
解析:选D 由图象可得A=,最小正周期T=4×=π,则ω==2.又f=sin=-,|φ|<,得φ=,则f(x)=sin,f=sin=sin
=-1,故选D.
2.(2017·天津高考)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f=2,f=0,且f(x)的最小正周期大于2π,则( )
A.ω=,φ= B.ω=,φ=-
C.ω=,φ=- D.ω=,φ=
解析:选A ∵f=2,f=0,
∴-=(2m+1),m∈N,
∴T=,m∈N,
∵f(x)的最小正周期大于2π,∴T=3π,
∴ω==,∴f(x)=2sin.
由2sin=2,得φ=2kπ+,k∈Z.
又|φ|<π,∴取k=0,得φ=.
[解题师说]
1.确定y=Asin(ωx+φ)+b(A>0,ω>0)中参数的方法
(1)求A,b:确定函数的最大值M和最小值m,则A=,b=;
(2)求ω:确定函数的周期T,则可得ω=;
(3)求φ:常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上).
②五点法:确定φ值时,往往以寻找“五点法”中的某一个点为突破口.具体如下:
第一点
图象上升时与x轴的交点
ωx+φ=0
第二点
图象的“峰点”
ωx+φ=
第三点
图象下降时与x
ωx+φ=π
轴的交点
第四点
图象的“谷点”
ωx+φ=
第五点
ωx+φ=2π
2.谨防1种失误
一般情况下,ω的值是唯一确定的,但φ的值是不确定的,它有无数个,如果求出的φ值不在指定范围内,可以通过加减的整数倍达到目的.
[冲关演练]
1.(2015·全国卷Ⅰ)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
解析:选D 由图象知,周期T=2=2,
∴=2,∴ω=π.
由π×+φ=+2kπ,得φ=+2kπ,k∈Z,
不妨取φ=,∴f(x)=cos.
由2kπ<πx+<2kπ+π,
得2k-<x<2k+,k∈Z,
∴f(x)的单调递减区间为,k∈Z.
2.(2018·西安八校联考)已知函数f(x)=sin(ωx+φ)的图象上的一个最高点和它相邻的一个最低点的距离为2,且过点,则函数f(x)=________.
解析:依题意得 =2,则=2,即ω=,所以f(x)=sin,由于该函数图象过点,因此sin(π+φ)=-,即sin φ=,而-≤φ≤,故φ=,所以f(x)=sin.
答案:sin
三角函数的图象与性质是高考的热点,常常利用其性质解决实际问题或与导数、不等式等综合构成较复杂的问题,此时题目难度大,综合性较强.,常见的命题角度有:
(1)三角函数模型的应用;
(2)函数零点(方程根)问题;
(3)三角函数图象与性质的综合应用.
[题点全练]
角度(一) 三角函数模型的应用
1.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+BA>0,ω>0,|φ|<的模型波动(x为月份),已知3月份达到最高价9千元,9月份价格最低为5千元.则7月份的出厂价格为________元.
解析:作出函数简图如图:
三角函数模型为:y=Asin(ωx+φ)+B,
由题意知:A=2 000,B=7 000,T=2×(9-3)=12,
∴ω==.
将(3,9 000)看成函数图象的第二个特殊点,
则有×3+φ=,∴φ=0,
故f(x)=2 000sinx+7 000(1≤x≤12,x∈N*).
∴f(7)=2 000×sin+7 000=6 000.
故7月份的出厂价格为6 000元.
答案:6 000
[题型技法]
三角函数模型在实际应用中体现的2个方面
(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与函数之间的对应法则;
(2)把实际问题抽象转化成数学问题,建立三角函数模型,再利用三角函数的有关知识解决问题,其关键是建模.
角度(二) 函数零点(方程根)问题
2.函数y=sin(ωx+φ)在同一个周期内,当x=时,y取得最大值1,当x=时,y取得最小值-1.
❶
若函数f(x)满足方程f(x)=a(0<a<1),则在[0,2π]内的
❷
所有实数根之和为( )
❸
A. B.
C. D.
[学审题]
①由在同一周期内给出y取得最大值、最小值时对应的x值,可推导出最小正周期T;
②在一个周期内有两个根满足f(x)=a,可结合图象推出两根关系;
③应想到在[0,2π]内有几个周期.
解析:选A 由题意可得=2×,所以ω=3.
又sin=1,所以+φ=2kπ+(k∈Z),
所以φ=2kπ-(k∈Z).
又|φ|<,所以φ=-,
所以函数f(x)=sin.
由于f(x)=sin的最小正周期为,
所以f(x)=sin在[0,2π]内恰有3个周期,
所以sin=a(0
0,ω>0);
(2)画出长度为一个周期的区间上的函数图象;
(3)利用图象解决有关三角函数的方程、不等式问题.
角度(三) 三角函数图象与性质的综合应用
3.(2018·湘中名校联考)已知函数f(x)=sin ωx-sin(ω>0).
(1)若f(x)在[0,π]上的值域为,求ω的取值范围;
(2)若f(x)在上单调,且f(0)+f=0,求ω的值.
解:f(x)=sin ωx-sin=sin ωx-sin ωx-cos ωx=sin ωx-cos ωx=sin.
(1)由x∈[0,π]⇒ωx-∈,又f(x)在[0,π]上的值域为,即最小值为-,最大值为1,则由正弦函数的图象可知≤ωπ-≤,解得≤ω≤.
∴ω的取值范围是.
(2)因为f(x)在上单调,
所以≥-0,则≥,
即ω≤3,又ω>0,所以0<ω≤3,
由f(0)+f=0且f(x)在上单调,得是f(x)图象的对称中心,
∴-=kπ,k∈Z⇒ω=6k+2,k∈Z,
又0<ω≤3,所以ω=2.
[题型技法]
解决三角函数图象与性质综合问题的步骤
(1)将f(x)化为asin x+bcos x的形式;
(2)构造f(x)=·sin x+·cos x;
(3)和角公式逆用,得f(x)=sin(x+φ)(其中φ为辅助角);
(4)利用f(x)=sin(x+φ)研究三角函数的性质;
(5)反思回顾,查看关键点、易错点和答题规范.
[冲关演练]
1.(2018·东北四市模拟)若关于x的方程2sin=m在上有两个不等实根,则m的取值范围是( )
A.(1,) B.[0,2]
C.[1,2) D.[1,]
解析:选C 2sin=m在上有两个不等实根等价于函数f(x)=2sin的图象与直线y=m有两个交点.在同一坐标系中作出y=f(x)与y=m的图象如图所示,由图可知m的取值范围是[1,2).
2.(2017·河北石家庄一模)若函数f(x)=sin(2x+θ)+cos(2x+θ)(0<θ<π)的图象关于点对称,则函数f(x)在上的最小值是( )
A.-1 B.-
C.- D.-
解析:选B f(x)=sin(2x+θ)+cos(2x+θ)=2sin,则由题意,知f=
2sin=0,又因为0<θ<π,所以<π+θ+<,所以π+θ+=2π,所以θ=,所以f(x)=-2sin 2x,又因为函数f(x)在上是减函数,所以函数f(x)在上的最小值为f=-2sin=-,故选B.
3.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-cost-sint,t∈[0,24),则实验室这一天的最大温差为________℃.
解析:因为f(t)=10-2=10-2sin,又0≤t<24,所以≤t+<,
所以-1≤sin≤1.
当t=2时,sin=1;
当t=14时,sin=-1.
于是f(t)在[0,24)上的最大值为12,最小值为8.
故实验室这一天最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃.
答案:4
(一)普通高中适用作业
A级——基础小题练熟练快
1.函数y=sin在区间上的简图是( )
解析:选A 令x=0,得y=sin=-,排除B、D.由f=0,f=0,排除C,故选A.
2.为了得到函数y=3sin 2x+1的图象,只需将y=3sin x的图象上的所有点( )
A.横坐标伸长2倍,再向上平移1个单位长度
B.横坐标缩短倍,再向上平移1个单位长度
C.横坐标伸长2倍,再向下平移1个单位长度
D.横坐标缩短倍,再向下平移1个单位长度
解析:选B 将y=3sin x的图象上的所有点的横坐标缩短倍得到y=3sin 2x的图象,再将y=3sin 2x的图象再向上平移1个单位长度即得y=3sin 2x+1的图象,故选B.
3.函数f(x)=tan ωx(ω>0)的图象的相邻两支截直线y=2所得线段长为,则f的值是( )
A.- B.
C.1 D.
解析:选D 由题意可知该函数的周期为,
∴=,ω=2,f(x)=tan 2x.
∴f=tan =.
4.若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω等于( )
A.5 B.4
C.3 D.2
解析:选B 由图象可知=x0+-x0=,即T==,故ω=4.
5.若函数f(x)=2sin ωx(ω>0)在(0,2π)上恰有两个极大值和一个极小值,则ω的取值范围是( )
A. B.
C. D.
解析:选A 因为函数f(x)在(0,2π)上恰有两个极大值和一个极小值,所以由正弦函数的图象可得T<2π≤T,即·<2π≤·,解得<ω≤.
6.将函数f(x)=cos 2x的图象向右平移个单位长度后得到函数g(x),则g(x)具有的性质是( )
A.最大值为1,图象关于直线x=对称
B.在上单调递增,为奇函数
C.在上单调递增,为偶函数
D.周期为π,图象关于点对称
解析:选B 将函数f(x)=cos 2x的图象向右平移个单位长度后得到函数g(x)=cos=sin 2x的图象,当x=时,g(x)=0,故A错,当x∈时,2x∈,故函数g(x)在上单调递增,为奇函数,故B正确,C错,当x=时,g(x)=,故D错,选B.
7.若函数f(x)=sin(ω>0)的最小正周期为,则f=________.
解析:由f(x)=sin(ω>0)的最小正周期为,得ω=4.所以f=sin=0.
答案:0
8.已知函数f(x)=2sin 的图象经过点(0,1),则该函数的振幅为____________,周期T为____________,频率为____________,初相φ为____________.
解析:振幅A=2,T==6,f=.
因为图象过点(0,1),
所以2sin φ=1,所以sin φ=,
又|φ|<,所以φ=.
答案:2 6
9.(2017·河南洛阳统考)函数f(x)=2sin(ωx+φ)的部分图象如图所示,已知图象经过点A(0,1),B,则f(x)=
____________.
解析:由已知得=,∴T=,
又T=,∴ω=3.
∵f(0)=1,∴sin φ=,又∵0<φ<,∴φ=,
∴f(x)=2sin(经检验满足题意).
答案:2sin
10.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+Acos(x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为________℃.
解析:依题意知,a==23,A==5,
所以y=23+5cos,
当x=10时,y=23+5cos=20.5.
答案:20.5
B级——中档题目练通抓牢
1.(2018·云南11校跨区调研)函数f(x)=sin ωx(ω>0)的图象向左平移个单位长度,所得图象经过点,则ω的最小值是( )
A. B.2
C.1 D.
解析:选C 依题意得,函数f=sin(ω>0)的图象过点,
于是有f=sinω=sin ωπ=0(ω>0),ωπ=kπ,k∈Z,即ω=k∈Z,
因此正数ω的最小值是1,选C.
2.(2018·安徽两校阶段性测试)将函数y=cos的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位长度,所得函数图象的一条对称轴为( )
A.x= B.x=
C.x= D.x=π
解析:选A 将函数y=cos的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=cos的图象;再将此函数的图象向左平移个单位长度后,得到函数y=cos=cos的图象.该函数图象的对称轴为-=kπ(k∈Z),即x=2kπ+(k∈Z).结合选项,只有A符合,故选A.
3.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,又x1,x2∈,且f(x1)=f(x2),则f(x1+x2)=( )
A. B.
C. D.1
解析:选B 由题图可知,=-=,则T=π,ω=2,又=,所以f(x)的图象过点,即sin=1,得+φ=+2kπ,k∈Z,即φ=+2kπ,k∈Z,又|φ|<,可得φ=,所以f(x)=sin.由f(x1)=f(x2),x1,x2∈,可得x1+x2=-+=,所以f(x1+x2)=f=sin=sin=.
4.若函数f(x)=sin(ωx+φ)的部分图象如图所示,直线x=是它的一条对称轴,则函数f(x)的解析式为________.
解析:由题意可知,=-=,
所以T==π,
所以ω=2.
又因为f=1,
所以sin=1,
所以+φ=+2kπ(k∈Z).
又φ∈,所以φ=,
所以f(x)=sin.
答案:f(x)=sin
5.已知函数f(x)=3sin(ω>0)和g(x)=3cos(2x+φ)的图象完全相同,若x∈,则f(x)的值域是________.
解析:f(x)=3sin=3cos=3cos,易知ω=2,则f(x)=3sin,
∵x∈,∴-≤2x-≤,
∴-≤f(x)≤3.
答案:
6.已知函数f(x)=2sin(其中0<ω<1),若点是函数f(x)图象的一个对称中心.
(1)求ω的值,并求出函数f(x)的增区间;
(2)先列表,再作出函数f(x)在区间[-π,π]上的图象.
解:(1)因为点是函数f(x)图象的一个对称中心,
所以-+=kπ(k∈Z),
所以ω=-3k+(k∈Z),因为0<ω<1,
所以当k=0时,可得ω=.
所以f(x)=2sin.
令2kπ-≤x+≤2kπ+(k∈Z),
解得2kπ-≤x≤2kπ+(k∈Z),
所以函数f(x)的增区间为(k∈Z).
(2)由(1)知,f(x)=2sin,x∈[-π,π].
列表如下:
x+
-
-
0
π
x
-π
-
-
π
y
-1
-2
0
2
0
-1
作出函数部分图象如图所示:
7.(2017·山东高考)设函数f(x)=sin+sin,其中0<ω<3.已知f=0.
(1)求ω;
(2)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在上的最小值.
解:(1)因为f(x)=sin+sin,
所以f(x)=sin ωx-cos ωx-cos ωx
=sin ωx-cos ωx
=
=sin.
因为f=0,
所以-=kπ,k∈Z.
故ω=6k+2,k∈Z.
又0<ω<3,所以ω=2.
(2)由(1)得f(x)=sin,
所以g(x)=sin=sin.
因为x∈,
所以x-∈,
当x-=-,即x=-时,g(x)取得最小值-.
C级——重难题目自主选做
1.(2018·湘中名校联考)已知函数f(x)=sin+,ω>0,x∈R,且f(α)=-,f(β)=.若|α-β|的最小值为,则函数的单调递增区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
解析:选B 由f(α)=-,f(β)=,|α-β|的最小值为,知=,即T=3π=,所以ω=,所以f(x)=sin+,令-+2kπ≤x-≤+2kπ(k∈Z),得-+3kπ≤x≤π+3kπ(k∈Z),故选B.
2.已知函数f(x)=Mcos(ωx+φ)(M >0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,AC=BC=,C=90°,则f的值为
________.
解析:依题意知,△ABC是直角边长为的等腰直角三角形,因此其边AB上的高是,函数f(x)的最小正周期是2,故M=,=2,ω=π,f(x)=cos(πx+φ).又函数f(x)是奇函数,于是有φ=kπ+(k∈Z).由0<φ<π,得φ=,故f(x)=-sin πx,f=-sin=-.
答案:-
(二)重点高中适用作业
A级——保分题目巧做快做
1.函数y=sin在区间上的简图是( )
解析:选A 令x=0,得y=sin=-,排除B、D.由f=0,f=0,排除C,故选A.
2.函数f(x)=tan ωx(ω>0)的图象的相邻两支截直线y=2所得线段长为,则f的值是( )
A.- B.
C.1 D.
解析:选D 由题意可知该函数的周期为,
∴=,ω=2,f(x)=tan 2x.
∴f=tan =.
3.(2018·洛阳调研)已知函数f(x)=Asin(ωx+φ)
的部分图象如图所示,则f(x)的解析式是( )
A.f(x)=sin B.f(x)=sin
C.f(x)=sin D.f(x)=sin
解析:选D 由图象可知=-=,
∴T=π,∴ω==2,故排除A、C;
把x=代入检验知,选项D符合题意.
4.(2016·全国卷Ⅱ)若将函数y=2sin 2x的图象向左平移个单位长度,则平移后图象的对称轴为( )
A.x=-(k∈Z) B.x=+(k∈Z)
C.x=-(k∈Z) D.x=+(k∈Z)
解析:选B 将函数y=2sin 2x的图象向左平移个单位长度,得到函数y=2sin =2sin的图象.由2x+=kπ+(k∈Z),得x=+(k∈Z),即平移后图象的对称轴为x=+(k∈Z).
5.将函数f(x)=2cos 2x的图象向右平移个单位得到函数g(x)的图象,若函数g(x)在区间和上均单调递增,则实数a的取值范围是( )
A. B.
C. D.
解析:选A 易得g(x)=2cos,由2kπ-π≤2x-≤2kπ,得kπ-≤x≤kπ+(k∈Z),即函数g(x)的单调增区间为(k∈Z).
当k=0时,函数的增区间为,
当k=1时,函数的增区间为.
又函数g(x)在区间和上均单调递增,所以解得≤a≤.
6.(2018·河南洛阳统考)函数f(x)=2sin(ωx+φ)的部分图象如图所示,已知图象经过点A(0,1),B,则f(x)=____________.
解析:由已知得=,∴T=,
又T=,∴ω=3.
∵f(0)=1,∴sin φ=,
又∵0<φ<,∴φ=,
∴f(x)=2sin(经检验满足题意).
答案:2sin
7.已知函数f(x)=3sin(ω>0)和g(x)=3cos(2x+φ)的图象完全相同,若x∈,则f(x)的值域是________.
解析:f(x)=3sin=3cos=3cos,易知ω=2,则f(x)=3sin,
∵x∈,∴-≤2x-≤,
∴-≤f(x)≤3.
答案:
8.(2018·山东师大附中模拟)设P为函数f(x)=sinx的图象上的一个最高点,Q为函数g(x)=cosx的图象上的一个最低点,则|PQ|的最小值是________.
解析:由题意知两个函数的周期都为T==4,由正、余弦函数的图象知,f(x)与g(x)的图象相差个周期,设P,Q分别为函数f(x),g(x)图象上的相邻的最高点和最低点,设P(
x0,1),则Q(x0+1,-1),则|PQ|min==.
答案:
9.已知函数f(x)=2sin(其中0<ω<1),若点是函数f(x)图象的一个对称中心.
(1)求ω的值,并求出函数f(x)的增区间;
(2)先列表,再作出函数f(x)在区间[-π,π]上的图象.
解:(1)因为点是函数f(x)图象的一个对称中心,
所以-+=kπ(k∈Z),
所以ω=-3k+(k∈Z),因为0<ω<1,
所以当k=0时,可得ω=.
所以f(x)=2sin.
令2kπ-≤x+≤2kπ+(k∈Z),
解得2kπ-≤x≤2kπ+(k∈Z),
所以函数的增区间为(k∈Z).
(2)由(1)知,f(x)=2sin,x∈[-π,π],
列表如下:
x+
-
-
0
π
x
-π
-
-
π
y
-1
-2
0
2
0
-1
作出函数部分图象如图所示:
10.(2018·黑龙江哈尔滨六中月考)已知函数f(x)=cos+2sinsin.
(1)求函数f(x)的单调递增区间;
(2)将y=f(x)的图象向左平移个单位长度,再将得到的图象横坐标变为原来的2倍(纵坐标不变),得到y=g(x)的图象.若函数y=g(x)在区间上的图象与直线y=a有三个交点,求实数a的取值范围.
解:(1)f(x)=cos+2sinsin
=cos 2x+sin 2x+(sin x-cos x)(sin x+cos x)
=cos 2x+sin 2x+sin2x-cos2x
=cos 2x+sin 2x-cos 2x
=sin.
令2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.
所以函数f(x)的单调递增区间是,k∈Z.
(2)将f(x)的图象向左平移个单位长度,得y=sin2)=sin=cos 2x的图象,再将得到的图象的横坐标变为原来的2倍(纵坐标不变),得g(x)=cos x的图象.
作函数g(x)=cos x在区间,上的图象,及直线y=a.根据图象知,实数a的取值范围是.
B级——拔高题目稳做准做
1.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,又x1,x2∈,且f(x1)=f(x2),则f(x1+x2)=( )
A. B.
C. D.1
解析:选B 由题图可知,=-=,则T=π,ω=2,又=,所以f(x)的图象过点,即sin=1,又|φ|<,可得φ=,所以f(x)=sin.由f(x1)=f(x2),x1,x2∈,可得x1+x2=-+=,所以f(x1+x2)=f=sin=sin=.
2.(2018·湘中名校联考)已知函数f(x)=sin+,ω>0,x∈R,且f(α)=-,f(β)=.若|α-β|的最小值为,则函数的单调递增区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
解析:选B 由f(α)=-,f(β)=,|α-β|的最小值为,知=,即T=3π=,所以ω=,所以f(x)=sin+,令-+2kπ≤x-≤+2kπ(k∈Z),得-+3kπ≤x≤π+3kπ(k∈Z),故选B.
3.已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤对x∈R恒成立,且f>f(π),则f(x)的单调递增区间是________.
解析:因为f(x)≤对x∈R恒成立,即==1,所以φ=kπ+
(k∈Z).因为f>f(π),所以sin(π+φ)>sin(2π+φ),即sin φ<0,所以φ=-+2kπ(k∈Z),所以f(x)=sin,所以由三角函数的单调性知2x-∈(k∈Z),
解得x∈(k∈Z).
答案:(k∈Z)
4.已知函数f(x)=2sin,g(x)=mcos-2m+3(m>0),若对∀x1∈,∃x2∈,使得g(x1)=f(x2)成立,则实数m的取值范围是________.
解析:当x∈时,2x+∈,sin∈,∴当x∈时,函数f(x)=2sin的值域为[1,2].当x∈时,2x-∈,cos∈,∴当x∈时,函数g(x)=mcos-2m+3(m>0)的值域为.∵对∀x1∈,∃x2∈,使得g(x1)=f(x2)成立,∴解得1≤m≤,即m∈.
答案:
5.已知函数f(x)=cos(πx+φ)的部分图象如图所示.
(1)求φ及图中x0的值;
(2)设g(x)=f(x)+f,求函数g(x)在区间上的最大值和最小值.
解:(1)由题图得f(0)=,所以cos φ=,
因为0<φ<,故φ=.
由于f(x)的最小正周期等于2,
所以由题图可知1<x0<2,
故<πx0+<.
由f(x0)=,得cos=,
所以πx0+=,x0=.
(2)因为f=cos=cos=-sin πx,
所以g(x)=f(x)+f=cos-sin πx
=cos πxcos-sin πxsin-sin πx
=cos πx-sin πx
=sin.
当x∈时,-≤-πx≤.
所以-≤sin≤1,
故-πx=,即x=-时,g(x)取得最大值;
当-πx=-,即x=时,g(x)取得最小值-.
6.如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC,另一侧修建一条休闲大道,它的前一段OD是函数y=k(k>0)图象的一部分,后一段DBC是函数y=AsinA>0,ω>0,|φ|<,x∈[4,8]的图象,图象的最高点为B,DF⊥OC,垂足为F.
(1)求函数y=Asin(ωx+φ)的解析式;
(2)若在草坪内修建如图所示的儿童游乐园,即矩形PMFE,问点P落在曲线OD上何处时,儿童游乐园的面积最大?
解:(1)对于函数y=Asin(ωx+φ),由图象可知,
A=,ω===,
将B代入y=sin中,
可得sin=1,
故+φ=2kπ+(k∈Z),φ=2kπ-(k∈Z).
因为|φ|<,所以φ=-.
故y=sin,x∈[4,8].
(2)在y=sin中,令x=4,得y=4,故D(4,4),从而得OD对应的函数为y=2(0≤x≤4).
设点P(0≤t≤4),
则矩形PMFE的面积S=t(0≤t≤4).
因为S′=4-,由S′=0,得t=,
当t∈时,S′>0,S单调递增;
当t∈时,S′<0,S单调递减.
所以当t=时,S最大,此时点P的坐标为.