六年级下册数学课件-2 圆柱和圆锥复习丨苏教版 (共37张PPT)

六年级下册数学课件-2 圆柱和圆锥复习丨苏教版 (共37张PPT)

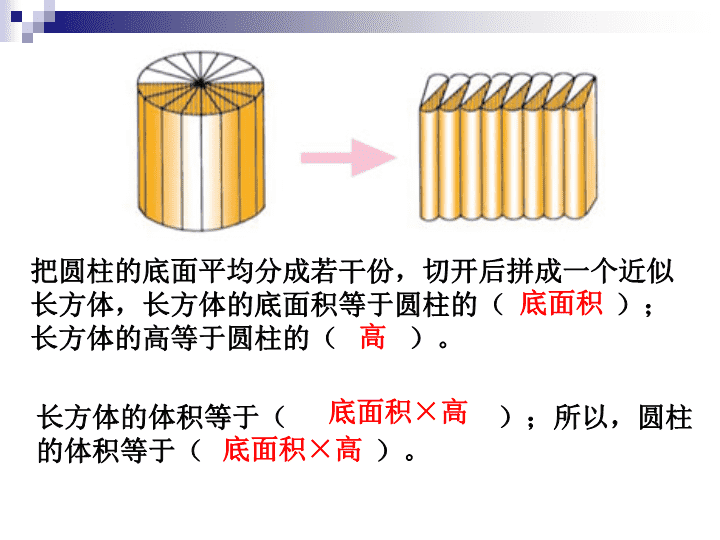
底面积 高 把圆柱的底面平均分成若干份，切开后拼成一个近似 长方体，长方体的底面积等于圆柱的（ ）； 长方体的高等于圆柱的（ ）。 长方体的体积等于（ ）；所以，圆柱 的体积等于（ ）。 底面积×高 底面积×高 圆 柱 圆 锥 特 征 底 面 两个大小相同的圆 一个圆 侧 面 一个曲面， 沿一条高展开是一个 长方形或正方形。 一个曲面； 展开是一个扇形。 高 两底面之间的距离； 有无数条，都相等。 从顶点到底面圆心的距离； 只有一条。 公 式 S侧=c h S表= S侧+2S底 V=S h V= S h 联 系 圆锥的体积等于与它等底等高的圆柱体积的 。 3 1 3 1 1.计算圆柱的表面积、体积和圆锥体的体积 （单位：厘米） 基础练习 圆柱：表面积：6 ╥ ×6+（6÷2）2 ╥ ×2 体积：（6÷2）2 ╥ ×6 圆锥： 体积： ×22 ╥ ×63 1 （只列式不计算） 2.口答，下面的问题各是求什么？ 一个圆柱形水桶，底面半径10分米， 高是20分米。 ①给这个水桶加个盖 ②给这个水桶加箍 ③给这个水桶的外面涂上油漆 ④这个水桶能装多少水 水桶的底面积 水桶的底面周长 水桶的侧面积和底面积 水桶的容积 基础练习 ①把一个圆柱的侧面展开，不可能是（ ） A.长方形   B.梯形   C.正方形   D.平行四边形 B ②一个圆柱的侧面展开以后正好是一个正方形，那么 圆柱的高等于它的底面（      ）。 A .半径     B.直径   C.周长    D.面积 c 基础练习 ③如下图，将一个底面直径4厘米，高5厘米的圆柱 切成两个完全相等的部分，（ ）切法表面积增 加的大。 A B B 3.选一选 一个圆柱和一个圆锥的底面积和体 积分别相等，已知圆柱体的高5厘米， 那么圆锥体的高是 ( )厘米。 一个圆柱和一个圆锥的高和体积分 别相等，已知圆锥的底面积是2.4平 方厘米，那么圆柱的底面积是 ( ) 平方厘米。 一个圆柱和一个圆锥等底等高，已 知圆锥的体积是18立方厘米，那么 圆柱的体积是 ( )立方厘米。54 15 0.8 基础练习 4.填一填 画一画 综合练习 ②一根长3米的圆木，截成三段，表面积增加0.48平 方米，这根圆木原来的体积是（ ）立方米。 0.8╥ 0.36 60 2 20 3 2 1.填一填 ③等底等高的一个圆柱和一个圆锥的体积的和是80立 方分米,这个圆柱的体积是( )立方分米,这个圆锥 的体积是( )立方分米。圆柱的体积比圆锥的体 积多（ ）倍，圆锥的体积比圆柱的体积少 。 ①圆锥形的一堆沙,绕沙堆走一圈是12.56米,高6分米, 这堆沙共( )立方米。 （ ） （ ） （3）如果每平方米种植番茄6棵，这个大棚可以种植番茄多少棵？ （4）每隔3米用一根竹竿做支撑，一个大棚需要多少根竹竿？ 综合练习 2.算一算 2 × 2╥ ×15 ÷ 2+22 ╥ =34 ╥（平方米） 22 ╥ ×15 ÷ 2=30 ╥ （立方米） 15 ÷ 3+1 =6（根） 2 × 2 ×15 × 6 =360（棵） 你知道吗？ 你知道吗？ 2 4 一根圆柱形木材长2米, 把它截成相等的 2个小圆柱后，表面积增加了62.8平方分 米，这个圆柱形木材原来的体积是多少 立方分米? 一根圆柱形木材长10分米, 沿底面直 径和高切开， 表面积增加80平方分米， 这个圆柱形木材原来的表面积是多少 平方分米? 拓展提升 一根圆柱形木材长2米, 把它截成相等的 2个小圆柱后，表面积增加了62.8平方分 米，这个圆柱形木材原来的体积是多少 立方分米? 一根圆柱形木材长10分米, 沿底面直 径和高切开， 表面积增加80平方分米， 这个圆柱形木材原来的表面积是多少 平方分米? 拓展提升 62.8÷2×20=628（立方分米） 2米=20分米 80÷2 ÷10=4（分米） 4 ╥ ×10+（4÷2）2 ╥ ×2=48 ╥（平方分米） 学校大厅有4根圆柱形柱子，每根柱子的底 面周长是25.12分米，高是5米。如果每平方 米需要油漆费0.5元，那么漆这4根柱子需要 油漆费多少元？ 有一种圆锥形容器，给里面装入1千 克水后，水面正好是圆锥高的一半，若要 将此容器装满水，还需注入多少千克水？ 拓展提升 提示：先求小圆锥的体积与大圆锥的体积的体积比 ●…… • … 知 识 要 点 圆 柱 圆 锥 底 面 两个大小相同的圆 一个圆 侧 面 一个曲面， 沿一条高展开是一个 长方形或正方形。 一个曲面； 展开是一个扇形。 高 两底面之间的距离； 有无数条，都相等。 从顶点到底面圆心的距离； 只有一条。 公 式 S侧=c h S表= S侧+2S底 V=S h V= S h 联 系 圆锥的体积等于与它等底等高的圆柱体积的 。 3 1 3 1 圆柱和圆锥的特征有什么相同点和不同点呢？ 名称 相同点 不同点 圆柱 底面都是圆 形，侧面是 曲面。 有两个底面；有无数条高； 侧面展开是一个长方形或 正方形 圆锥 只有一个底面、一条高；侧 面展开是一个扇形； 有一种饮料瓶的瓶身呈圆柱形，容积是4升， 瓶中有一些饮料，正放时饮料高为20厘米，倒 放时空余部分为5厘米，求瓶中的饮料为多少升？ 拓展提升 有一种饮料瓶的瓶身呈圆柱形，容积是4升， 瓶中有一些饮料，正放时饮料高为20厘米，倒 放时空余部分为5厘米，求瓶中的饮料为多少升？ 5 20 拓展提升 一根圆柱形木材长2米, 把它截成相等的 2个小圆柱后，表面积增加了62.8平方分 米，这个圆柱形木材原来的体积是多少 立方分米? 一根圆柱形木材长10分米, 沿底面直 径和高切开， 表面积增加80平方分米， 这个圆柱形木材原来的表面积是多少 平方分米? 拓展提升 1.计算下面圆柱的表面积和体积 2、计算下面圆锥体的体积 （单位：厘米） （单位：厘米 ） 基础练习 圆柱：表面积：6 ╥ ×6+（6÷2）2 ╥ ×2=54 ╥（平方厘米） 体积：（6÷2）2 ╥ ×6=54 ╥（立方厘米） 圆锥： 体积： ×22 ╥ ×6=8 ╥（立方厘米）3 1 4 8 6 求出下面图形的体积。( 单位:厘米) 拓展提升 （4÷2）2 ╥ ×（6+8）÷2 =4╥ ×14 ÷2 =28╥ （立方厘米） （4÷2）2 ╥ ×[（6+8） ÷2] =4╥ ×7 =28╥ （立方厘米） 一个圆柱体削成一个最大的圆锥体，这个圆锥体 的体积是12立方分米，削去部分的体积是（ ）立 方分米。 一个正方体体削成一个最大的圆锥体，这个正方 体的棱长是6分米，削去部分的体积是（ ） 立方分米。 24 216-18╥ 159.48 底 面 两个大小相同的圆 一个圆 侧 面 一个曲面， 沿一条高展开是一个 长方形或正方形。 一个曲面； 展开是一个扇形。 高 两个底面之间的距离； 有无数条，都相等。 从顶点到底面圆 心的距离；只有 一条。 把圆柱的底面平均分成若干份，切开后拼成一个近似 长方体，长方体的底面积等于圆柱的（ ）； 长方体的高等于圆柱的（ ）。 长方体的长等于圆柱（ ）；长方体 的宽等于圆柱的（ ）。 拼好之后，（ ）不变；（ ）变（ ）了。 底面积 高 体积 表面积 大 底面半径 底面周长的一半 ①圆锥形的一堆沙,底面周长是12.56米,高6分米,这 堆沙共( )立方分米。 综合练习 ②一根长3米的圆木，截成三段，表面积增加0.48平 方米，这根圆木原来的体积是（ ）立方米。 ③把一个棱长6分米的正方体体削成一个最大的圆柱 体，圆柱的体积是（ ）立方分米。再将圆柱削 成一个最大的圆锥，还要再削去（ ）立方分米。 800╥ 0.36 54╥ 36╥ 60 2 20 3 2 1.填一填 ④等底等高的一个圆柱和一个圆锥的体积的和是80立 方分米,这个圆柱的体积是( )立方分米,这个圆锥 的体积是( )立方分米。圆柱的体积比圆锥的体 积多（ ）倍，圆锥的体积比圆柱的体积少（ ）。