高考定积分分类汇总及答案
第十四节 定积分与微积分基本定理(理)
一、选择题1.(2013·江西卷)若S1=x2dx,S2=dx,S3=exdx,则S1,S2,S3的大小关系为( )
A.S1
3>S1>S2.故选B.
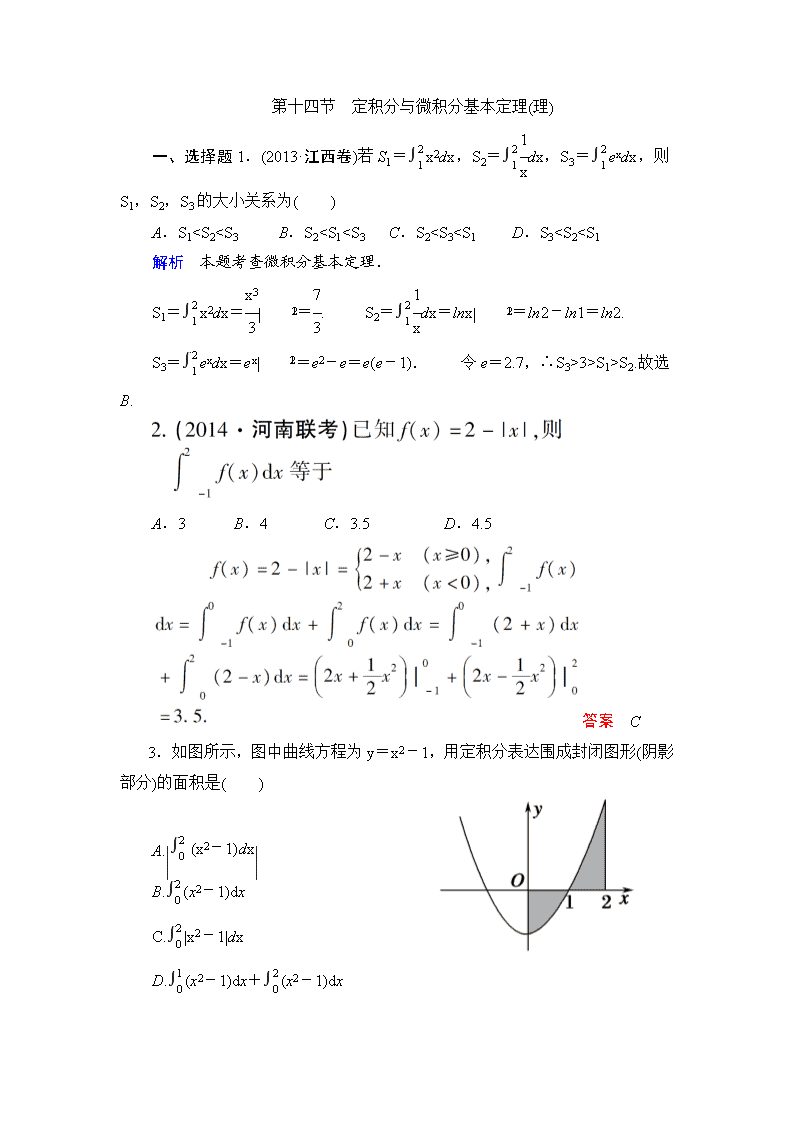
A.3 B.4 C.3.5 D.4.5
答案 C
3.如图所示,图中曲线方程为y=x2-1,用定积分表达围成封闭图形(阴影部分)的面积是( )
A.
B.(x2-1)dx
C.|x2-1|dx
D.(x2-1)dx+(x2-1)dx
解析 面积S=(1-x2)dx+(x2-1)dx=|x2-1|dx,故选C.
4.(2012·湖北卷)已知二次函数y=f(x)的图象如图所示,则它与x
轴所围图形的面积为( )
A. B. C. D.
5.(2013·湖北卷)一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7-3t+(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
A.1+25ln5 B.8+25ln
C.4+25ln5 D.4+50ln2
解析 令v(t)=0,7-3t+=0
∴3t2-4t-32=0,∴t=4,则汽车行驶的距离为v(t)dt=dt=
=7×4-×42+25ln5-0=4+25ln5,故选C.
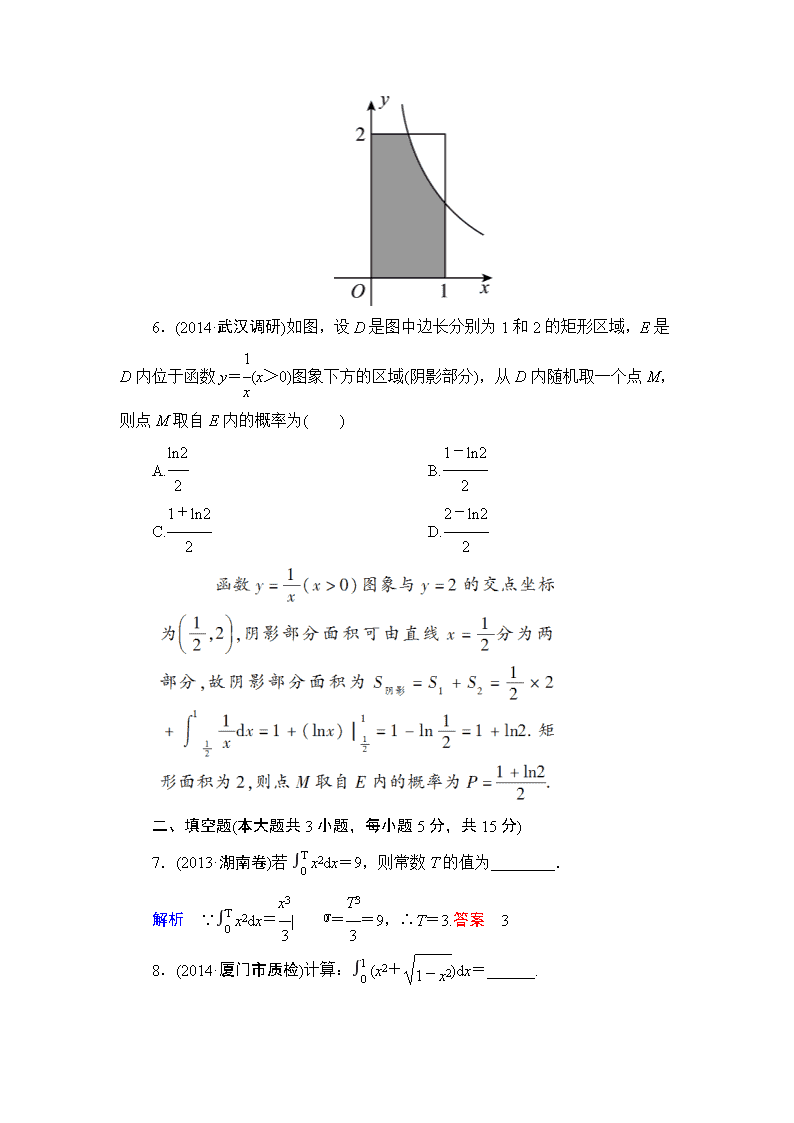
6.(2014·武汉调研)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
A. B.
C. D.
二、填空题(本大题共3小题,每小题5分,共15分)
7.(2013·湖南卷)若x2dx=9,则常数T的值为________.
解析 ∵x2dx===9,∴T=3.答案 3
8.(2014·厦门市质检)计算:(x2+)dx=______.
解析 (x2+)dx=x2dx+dx=+π=+.
9.已知函数y=f(x)的图象是折线段ABC,其中A(0,0)、B、C(1,0).函数y=xf(x)(0≤x≤1)的图象与x轴围成的图形的面积为________.
解析 设直线为y=kx+b,代入A,B两点,得y=10x.
代入B,C两点,则∴k=-10,b=10.
∴f(x)=∴y=xf(x)=
三、解答题(本大题共3小题,每小题10分,共30分)
10.若f(x)是一次函数,且f(x)dx=5,xf(x)dx=,求dx的值.
解 ∵f(x)是一次函数,∴设f(x)=ax+b(a≠0).
由(ax+b)dx=5,得=a+b=5.①
由xf(x)dx=,得(ax2+bx)dx=.
即=.
∴a+b=.②
解①②,得a=4,b=3.∴f(x)=4x+3.
于是dx=dx=(4+)dx
=(4x+3lnx)|=8+3ln2-4
=4+3ln2.
11.(2013·日照调研)如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.
解 抛物线y=x-x2与x轴两交点的横坐标x1=0,x2=1,
所以抛物线与x轴所围图形的面积
S=(x-x2)dx==-=.
又可得抛物线y=x-x2与y=kx两交点的横坐标为x′1=0,x′2=1-k,
所以=∫(x-x2-kx)dx
=
=(1-k)3.
又知S=,所以(1-k)3=.
于是k=1- =1-.
12.设函数f(x)=x3+ax2+bx在点x=1处有极值-2.
(1)求常数a,b的值;
(2)求曲线y=f(x)与x轴所围成的图形的面积.
解 (1)由题意知,f′(x)=3x2+2ax+b,f(1)=-2,且f′(1)=0,
即解得
(2)由(1)可知,f(x)=x3-3x.
作出曲线y=x3-3x的草图如图,
所求面积为阴影部分的面积,由x3-3x=0得曲线y=x3-3x与x轴的交点坐标是(-,0),(0,0)和(,0),而y=x3-3x是R上的奇函数,所以函数图象关于原点成中心对称.
所以所求图形的面积为