- 2021-04-12 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
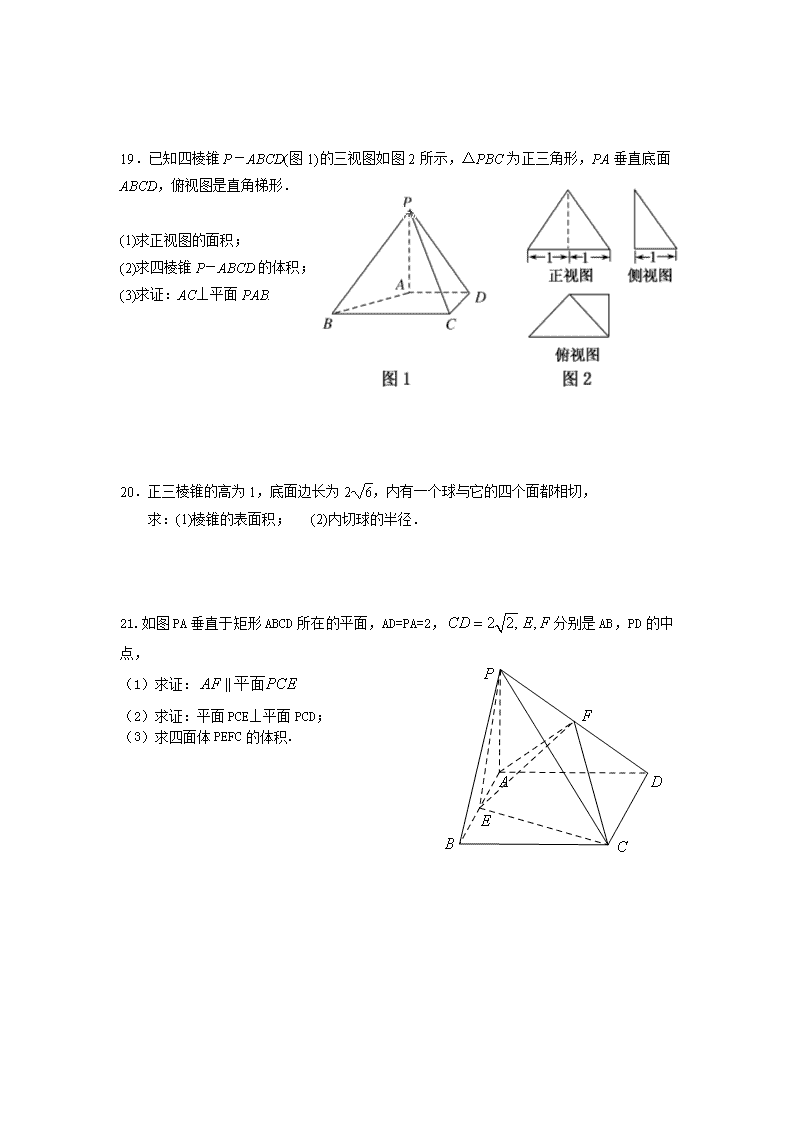
数学卷·2019届浙江省东阳中学高二10月阶段性检测(2017-10)
东阳中学2017-2018学年10月阶段测试考试卷 数学 命题人:李军红 审题人:李军红 一、 选择题:(每题4分,共40分) 1. 小明在上海世博会参观时,看到一个几何体,它的轴截面一定是圆面,则这个几何体是 A.圆柱 B.圆锥 C.球 D.圆台 2. 长方体的三个面的面积分别是,则长方体的对角线长是( ) A. B. C. D. 3.设l为直线,α,β是两个不同的平面,下列命题中正确的是( ) A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥β C.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β 4.下列说法中不正确的是( ) A.若一条直线垂直于一个三角形的两边,则一定垂直于第三边 B.同一个平面的两条垂线一定共面[来源] C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内 D.过一条直线有且只有一个平面与已知平面垂直 5. 若正四棱锥S-ABCD的三视图中,正视图、侧视图都是腰为,底边为2的等腰三角形,俯视图是边长为2的正方形,则正四棱锥S-ABCD的侧面积为( ) A. B. C. 1 D.2 6. 半径为的半圆卷成一个圆锥,则它的体积为( ) A. B. C . D. 7.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( ) A.若α⊥β,α∩β=n,m⊥n,则m⊥α B.若m⊂α,n⊂β,m∥n,则α∥β C.若m∥α,n∥β,m⊥n,则α⊥β D.若n⊥α,n⊥β, m⊥β,则m⊥α 8.小蚂蚁的家住在长方体ABCD—A1B1C1D1的A处,小蚂蚁的奶奶家住在C1处,三条棱长分别是AA1=1,AB=2,AD=4,小蚂蚁从A点出发,沿长方体的表面到小蚂蚁奶奶家C1的最短矩离是 ( ) A.5 B.7 C. D. 9. 一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为,,,则等于( ) A. B. C. D. 10.如图,正方体ABCD—A1B1C1D1的棱长为1,线段B1D1上有两个动点 E,F,且EF=,则下列结论错误的是( ) A.AC⊥BE B.EF∥平面ABCD C.三棱锥A—BEF的体积为定值 D.△AEF的面积与△BEF的面积相等 二、填空题:(每空4分,共36分) 11. 若直线a, b与直线c相交成等角,则a, b的位置关系是 . 12. 空间中三个平面最少把空间分成 部分;最多把空间分成 部分. 13. 等边三角形的边长为a,它绕其一边所在的直线旋转一周,则所得旋转体的体积为 ________. 14.在长方体ABCD-A1B1C1D1中,AB=BC=3,AA1=4,则异面直线AB1与 A1D所成的角的余弦值为 ;该长方体外接球的表面积为 . 15. 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图 是直角梯形(如图所示),, 则这块菜地的面积为_____________. 16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入 水中后,水面升高9厘米,则此球的半径为 . 17.已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起使二面角A-BD-C为120°,则点A到△BCD所在平面的距离为__________. 三、解答题:(18题14分,其余各题15分,共74分) 18.如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1中点. 求证:(1)平面ADE⊥平面BCC1B1; (2)直线A1F∥平面ADE. 19.已知四棱锥P-ABCD(图1)的三视图如图2所示,△PBC为正三角形,PA垂直底面ABCD,俯视图是直角梯形. [来源] (1)求正视图的面积; (2)求四棱锥P-ABCD的体积; (3)求证:AC⊥平面PAB. 20.正三棱锥的高为1,底面边长为2,内有一个球与它的四个面都相切, 求:(1)棱锥的表面积; (2)内切球的半径. 21.如图PA垂直于矩形ABCD所在的平面,AD=PA=2,分别是AB,PD的中点, (1)求证: (2)求证:平面PCE⊥平面PCD; (3)求四面体PEFC的体积. 22.已知四棱锥的底面为直角梯形,,底面 ,且,是的中点. (Ⅰ)证明:面面; (Ⅱ)求与所成角的余弦值; (Ⅲ)求面与面所成二面角的余弦值.查看更多