- 2021-04-12 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【三维设计】2017届高三数学(理)二轮复习(通用版)课余自主加餐训练 “12+4”限时提速练(七)
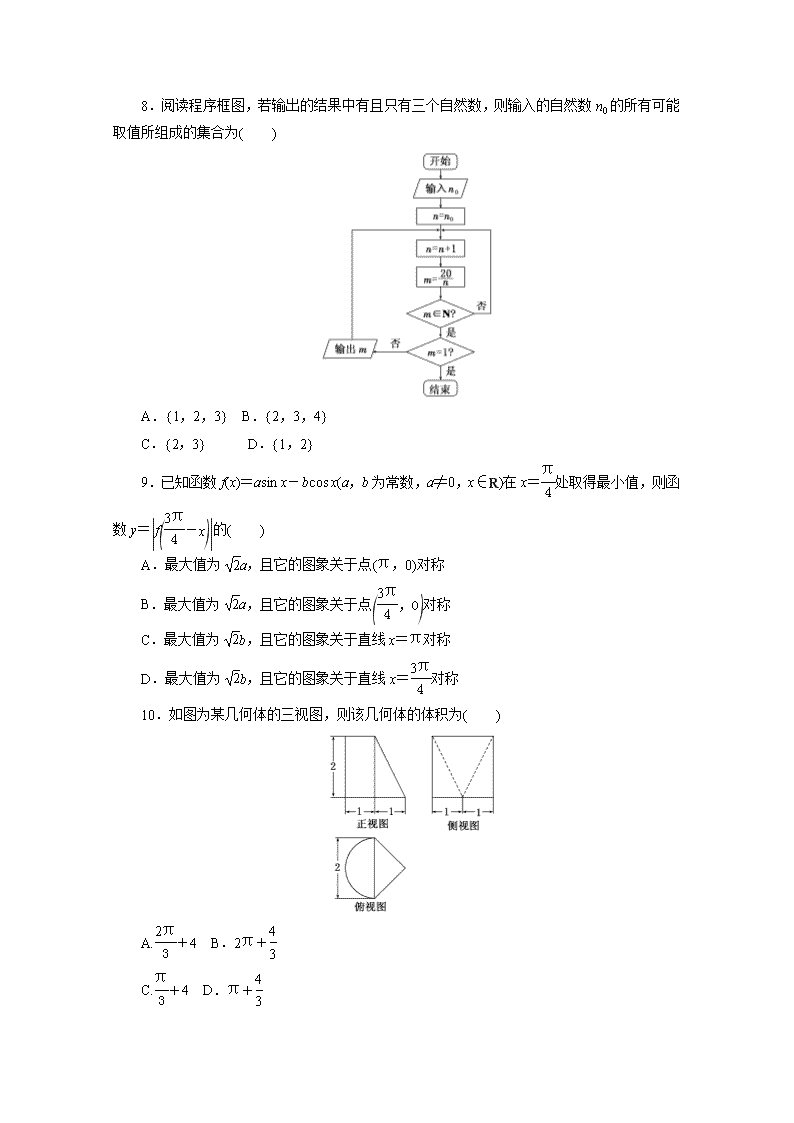
“12+4”限时提速练(七) 一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设全集U=R,集合A={x|x2-2x≥0},B={x|y=log2(x2-1)},则(∁UA)∩B=( ) A.[1,2) B.(1,2) C.(1,2] D.(-∞,-1)∪[0,2] 2.已知i为虚数单位,若复数z=的虚部为-3,则|z|=( ) A. B.2 C. D.5 3.若定义域为R的函数f(x)不是偶函数,则下列命题中一定为真命题的是( ) A.∀x∈R,f(-x)≠f(x) B.∀x∈R,f(-x)=-f(x) C.∃x0∈R,f(-x0)≠f(x0) D.∃x0∈R,f(-x0)=-f(x0) 4.已知sin=-,则2sin2-1=( ) A. B.- C. D.± 5.某学校为了提高学生的安全意识,防止安全事故的发生,拟在未来连续7天中随机选择3天进行紧急疏散演练,则选择的3天中恰好有2天连续的概率是( ) A. B. C. D. 6.已知双曲线-=1(a>0,b>0)的一条渐近线与直线3x-4y-5=0垂直,则双曲线的离心率为( ) A.或 B. C. D. 7.等比数列{an}的前n项和为Sn.已知S3 = a2 +10a1 ,a5=9,则a1=( ) A. B.- C. D.- 8.阅读程序框图,若输出的结果中有且只有三个自然数,则输入的自然数n0 的所有可能取值所组成的集合为( ) A.{1,2,3} B.{2,3,4} C.{2,3} D.{1,2} 9.已知函数f(x)=asin x-bcos x(a,b为常数,a≠0,x∈R)在x=处取得最小值,则函数y=的( ) A.最大值为a,且它的图象关于点(π,0)对称 B.最大值为a,且它的图象关于点对称 C.最大值为b,且它的图象关于直线x=π对称 D.最大值为b,且它的图象关于直线x=对称 10.如图为某几何体的三视图,则该几何体的体积为( ) A.+4 B.2π+ C.+4 D.π+ 11.设等比数列{an}的前n项和为Sn,M=S+S,N=Sn(S2n+S3n),则M与N的大小关系是( ) A.M≥N B.N≥M C.M=N D.不确定 12.已知函数f(x)=x2+ex-(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则实数a的取值范围是( ) A. B.(-∞,) C. D. 二、填空题(本大题共4小题,每小题5分) 13.已知向量的夹角为120°,且||=2,||=3,若,且,则实数λ的值为________. 14.(2-)6的展开式中x2的系数是________. 15.已知点P是抛物线C1:y2=4x上的动点,过点P作圆C2:(x-3)2+y2=2的两条切线,则两切线夹角的最大值为________. 16.在△ABC中,是2B与2C的等差中项,AB=,角B的平分线BD=,则BC=________. 答 案 一、选择题 1.解析:选B 由已知得A=(-∞,0]∪[2,+∞),∴∁UA=(0,2),又B=(-∞,-1)∪(1,+∞),∴(∁UA)∩B=(1,2),故选B. 2.解析:选C ∵z====-i, ∴-=-3,∴a=5,∴z=-2-3i,∴|z|==,故选C. 3.解析:选C 定义域为R的偶函数的定义:∀x∈R,f(-x)=f(x),这是一个全称命题,所以它的否定为特称命题:∃x0∈R,f(-x0)≠f(x0),故选C. 4.解析:选A 法一:∵sin=-,∴cos θ=-,∴2sin2-1=-cos θ=,故选A. 法二:特殊值法,取+θ=, ∴θ=,2sin2-1=2×-1=,故选A. 5.解析:选D 连续7天中随机选择3天,有C=35种情况,其中恰好有2天连续,有4+3+3+3+3+4=20种情况,所以所求的概率为=,故选D. 6.解析:选C 直线3x-4y-5=0的斜率为,∴双曲线的一条渐近线的斜率为-,即-=-,∴b=a,∴c==a,∴e==,故选C. 7. 解析:选C 由题知q≠1,则S3==a1q+10a1,得q2=9,又a5=a1q4=9,则a1=,故选C. 8.解析:选C 法一:要使输出的结果中有且只有三个自然数,只能是5,4,2,所以应使5≤<10,解得1<n0≤3,即n0=2,3,所以输入的自然数n0的所有可能值为2,3,故选C. 法二:代入验证法,当n0=1时,输出的结果是10,5,4,2,排除选项A,D,当n0=4时,输出的结果是4,2,排除选项B,故选C. 9.解析:选C 由条件得f=f(0),∴a=-b,∴f(x)=asin x+acos x=asin.又f(x)在x=处取得最小值,∴a<0,b>0,∴y===|asin x|=b|sin x|,故选C. 10.如图为某几何体的三视图,则该几何体的解析:选D 由三视图可知,该几何体是一个半圆柱与一个四棱锥的组合体,如图所示,其中四棱锥的底面ABCD为圆柱的轴截面,顶点P在半圆柱所在圆柱OO1的底面圆上,且点P在AB上的射影为底面圆的圆心O. 由三视图中的数据可得,半圆柱所在圆柱的底面半径r=1,母线长l=2, 故半圆柱的体积V1=πr2l=π×12×2=π; 四棱锥的底面ABCD是边长为2的正方形,PO⊥底面ABCD,且PO=r=1, 故其体积V2=S正方形ABCD×PO=×22×1=. 故该几何体的体积V=V1+V2=π+. 11.解析:选C 对于等比数列1,-1,1,-1,1,-1,…,S2k=0,S4k-S2k=0,S8k-S4k=0,令n=2k,此时有M=N=0;对于Sn,S2n-Sn,S3n-S2n,…,各项均不为零时, ∵等比数列{an}的前n项和为Sn,设{an}的公比为q,∴Sn,S2n-Sn,S3n-S2n是一个公比为qn的等比数列,∴S2n-Sn=Sn×qn,S3n-S2n=Sn×q2n,∴M=S+S=S×[1+(1+qn)2]=S×(2+2qn+q2n)=Sn×(S2n+S3n)=N,由上可知,M=N,选C. 12.解析:选B 法一:由题意可得,存在x<0,使得x2+ex-=(-x)2+ln(-x+a)成立,即ex-=ln(-x+a),ex--ln(-x+a)=0,令h(x)=ex--ln(-x+a),若a>0,则问题等价于h(x)=ex--ln(-x+a)在(-∞,0)上存在零点,易证h(x)在(-∞,0)上单调递增,当x趋近于-∞时,ex趋近于0,ln(-x+a)趋近于+∞,∴h(x)趋近于-∞,∴只需h(0)>0,即1--ln a>0⇒0<a<.若a≤0,则问题等价于h(x)=ex--ln(-x+a)在(-∞,a)上存在零点,易证h(x)在(-∞,a)上单调递增,当x趋近于-∞时,ex趋近于0,ln(-x+a)趋近于+∞,∴h(x)趋近于-∞,∴只需当x趋近于a时,h(x)>0,易得当x趋近于a时,h(x)趋近于+∞,∴a≤0符合题意.综上所述,实数a的取值范围是(-∞,),故选B. 法二:特殊值法和排除法,由题意可得,存在x<0,使得x2+ex-=(-x)2+ln(-x+a)成立,即ex-=ln(-x+a),ex--ln(-x+a)=0,令h(x)=ex--ln(-x+a),取a=1,h(0)=>0,h(-1)=--ln 2<0,∴由零点存在性定理可得a=1满足题意,排除选项A、C、D,故选B. 二、填空题 13.解析: ⇒-3λ-4λ+9+3=0⇒λ=. 答案: 14.解析:(2-)6展开式的通项为Tr+1=C·26-r·(-)r=(-1)r·26-r·C·x,分别取r=6,r=2,得(2-)6的展开式中含x2的项为·x3+x·24·C·x=243x2,故系数为243. 答案:243 15.解析:由已知得,圆心C2(3,0),半径为.设点P,两切点分别为A,B,要使两切线的夹角最大,只需|PC2|最小,|PC2|==,当y=4时,|PC2|min=2,∴∠APC2=∠BPC2=,∴∠APB=. 答案: 16.解析:在△ABC中,∵是2B与2C的等差中项,∴A=2(B+C),而A+B+C=180°,∴A=120°.在△ABD中,由正弦定理得=,∴sin∠ADB==, ∴∠ADB=45°,∴∠ABD=15°,∴∠ABC=30°,∴∠ACB=30°,∴AC=AB=, ∴在△ABC中,由余弦定理得BC==. 答案:查看更多