- 2021-04-12 发布 |
- 37.5 KB |
- 7页


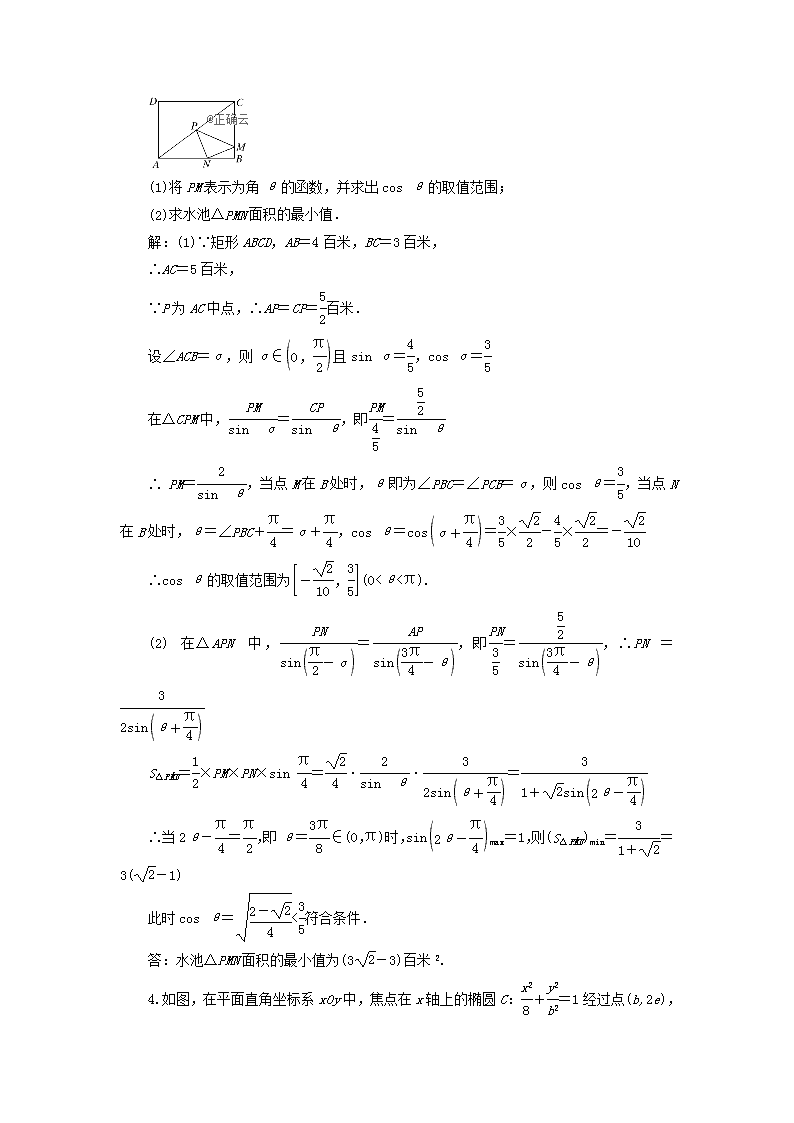
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届江苏省高考数学二轮复习综合仿真练(三)
综合仿真练(三) 1.已知向量m=(cos x,-1),n=(sin x,cos2x). (1)当x=时,求m·n的值; (2)若x∈,且m·n=-,求cos 2x的值. 解:(1)当x=时,m=,n=, 所以m·n=-=. (2)m·n=cos xsin x-cos2x=sin 2x-cos 2x-=sin-, 若m·n=-,则sin-=-, 即sin=, 因为x∈,所以-≤2x-≤, 所以cos=, 则cos 2x=cos=cos×cos-sinsin=×-×=. 2.如图,三棱柱ABCA1B1C1中,M,N分别为AB,B1C1的中点. (1)求证:MN∥平面AA1C1C; (2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB⊥平面CMN. 证明:(1)法一: 取A1C1的中点P,连结AP,NP. 因为C1N=NB1,C1P=PA1, 所以NP∥A1B1,NP=A1B1. 在三棱柱ABCA1B1C1中,A1B1∥AB,A1B1=AB. 所以NP∥AB,且NP=AB. 因为M为AB的中点,所以AM=AB. 所以NP=AM,且NP∥AM, 所以四边形AMNP为平行四边形,所以MN∥AP. 因为AP⊂平面AA1C1C,MN⊄平面AA1C1C, 所以MN∥平面AA1C1C. 法二: 取BC的中点Q,连结NQ,MQ. 由三棱柱可得,四边形BCC1B1为平行四边形. 又Q,N分别为BC,B1C1的中点, 所以CQ∥C1N,CQ=C1N, 所以四边形CQNC1为平行四边形. 所以NQ∥CC1. 因为NQ⊂平面MNQ,CC1⊄平面MNQ, 所以CC1∥平面MNQ. 因为AM=MB,CQ=QB,所以MQ∥AC. 同理可得AC∥平面MNQ. 因为AC⊂平面AA1C1C,CC1⊂平面AA1C1C,AC∩CC1=C,所以平面MNQ∥平面AA1C1C. 因为MN⊂平面MNQ,所以MN∥平面AA1C1C. (2)因为CA=CB,M为AB的中点,所以CM⊥AB. 因为CC1=CB1,N为B1C1的中点,所以CN⊥B1C1. 在三棱柱ABCA1B1C1中,BC∥B1C1,所以CN⊥BC. 因为平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC,CN⊂平面CC1B1B,所以CN⊥平面ABC. 因为AB⊂平面ABC,所以CN⊥AB. 因为CM⊂平面CMN,CN⊂平面CMN,CM∩CN=C, 所以AB⊥平面CMN. 3.(2019·海门中学模拟)某城市有一矩形街心广场ABCD,其中AB=4百米,BC=3百米,在其中心P处(AC中点)有一观景亭.现将挖掘一个三角形水池PMN种植荷花,其中M点在BC边上,N点在AB边上,满足∠MPN=45°.设∠PMC=θ. (1)将PM表示为角θ的函数,并求出cos θ的取值范围; (2)求水池△PMN面积的最小值. 解:(1)∵矩形ABCD,AB=4百米,BC=3百米, ∴AC=5百米, ∵P为AC中点,∴AP=CP=百米. 设∠ACB=α,则α∈且sin α=,cos α= 在△CPM中,=,即= ∴ PM=,当点M在B处时,θ即为∠PBC=∠PCB=α,则cos θ=,当点N在B处时,θ=∠PBC+=α+,cos θ=cos=×-×=- ∴cos θ的取值范围为(0<θ<π). (2)在△APN中,=,即=,∴PN= S△PMN=×PM×PN×sin =··= ∴当2θ-=,即θ=∈(0,π)时,sinmax=1,则(S△PMN)min==3(-1) 此时cos θ=<符合条件. 答:水池△PMN面积的最小值为(3-3)百米2. 4.如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:+=1经过点(b,2e),其中 e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方). (1)求椭圆C的标准方程; (2)过点O且平行于l的直线交椭圆C于点M,N,求的值; (3)记直线l与y轴的交点为P.若=,求直线l的斜率k. 解:(1)因为椭圆C:+=1经过点(b,2e), 所以+=1. 因为e2==,所以+=1, 又a2=b2+c2,+=1, 解得b2=4或b2=8(舍去). 所以椭圆C的方程为+=1. (2)设A(x1,y1),B(x2,y2). 因为T(1,0),则直线l的方程为y=k(x-1). 联立直线l与椭圆方程消去y, 得(2k2+1)x2-4k2x+2k2-8=0, 所以x1+x2=,x1x2=. 因为MN∥l,所以直线MN的方程为y=kx, 联立直线MN与椭圆方程消去y得(2k2+1)x2=8,解得x2=. 因为MN∥l,所以=, 因为(1-x1)·(x2-1)=-[x1x2-(x1+x2)+1]=,(xM-xN)2=4x2=. 所以=×=. (3)在y=k(x-1)中,令x=0,则y=-k,所以P(0,-k), 从而=(-x1,-k-y1),=(x2-1,y2), ∵=,∴-x1=(x2-1), 即x1+x2=,① 由(2)知x1+x2=,② 联立①②得x1=,x2=. 又x1x2=, ∴50k4-83k2-34=0, 解得k2=2或k2=-(舍去). 又因为k>0,所以k=. 5.数列{an}中,对任意给定的正整数n,存在不相等的正整数i,j(i查看更多