生活中的平面图形教案

生活中的平面图形教案

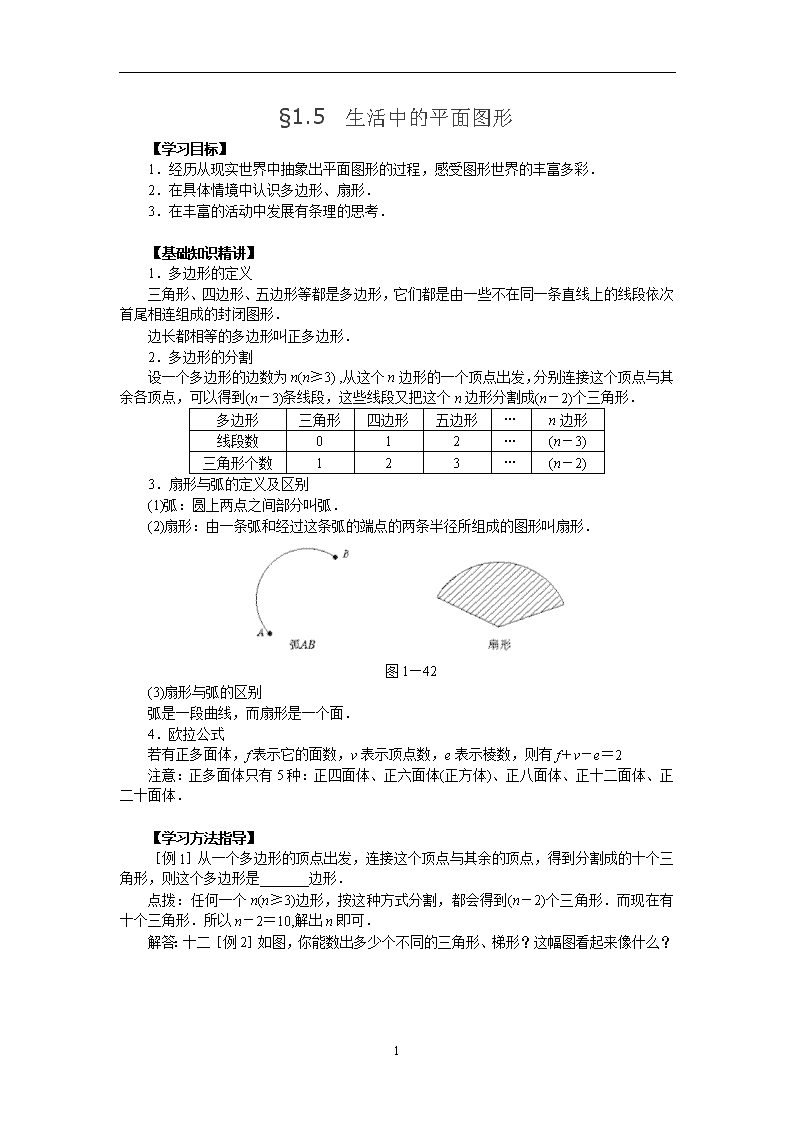
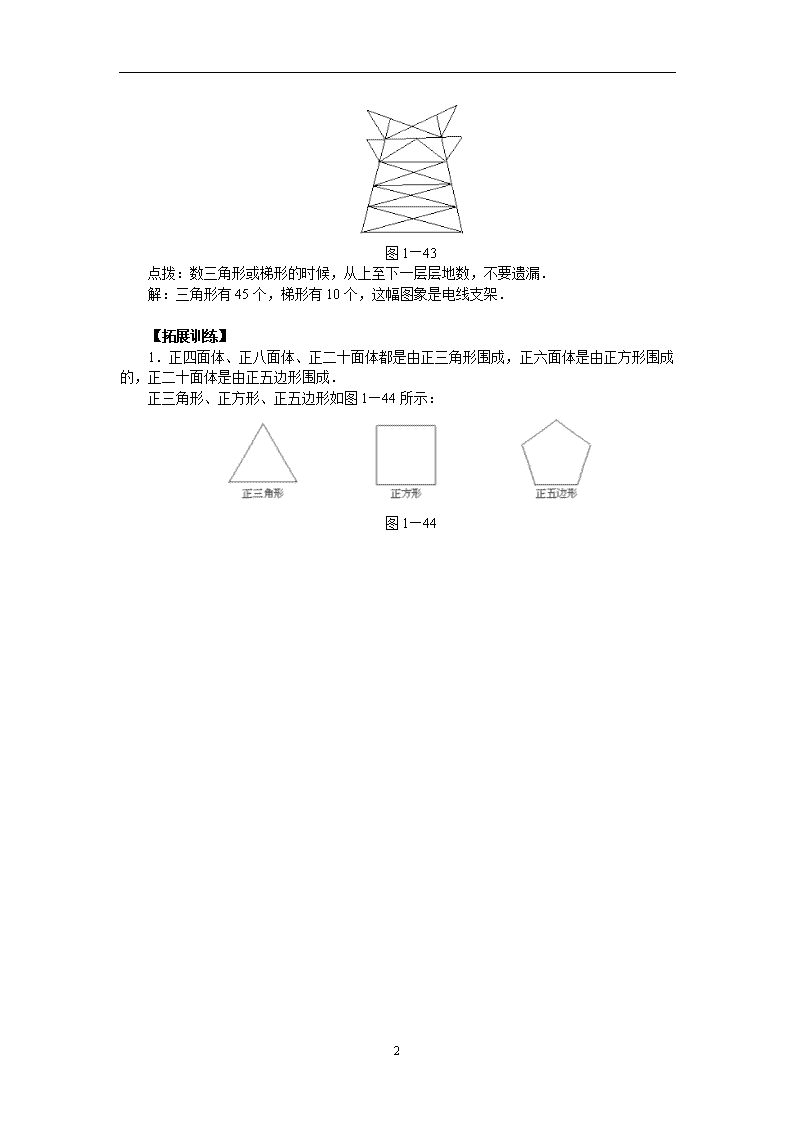
‎ ‎ ‎§1.5  生活中的平面图形 ‎【学习目标】‎ ‎1．经历从现实世界中抽象出平面图形的过程，感受图形世界的丰富多彩．‎ ‎2．在具体情境中认识多边形、扇形．‎ ‎3．在丰富的活动中发展有条理的思考．‎ ‎【基础知识精讲】‎ ‎1．多边形的定义 三角形、四边形、五边形等都是多边形，它们都是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形．‎ 边长都相等的多边形叫正多边形．‎ ‎2．多边形的分割 设一个多边形的边数为n(n≥3) ,从这个n边形的一个顶点出发，分别连接这个顶点与其余各顶点，可以得到(n－3)条线段，这些线段又把这个n边形分割成(n－2)个三角形．‎ 多边形 三角形 四边形 五边形 ‎…‎ n边形 线段数 ‎0‎ ‎1‎ ‎2‎ ‎…‎ ‎(n－3)‎ 三角形个数 ‎1‎ ‎2‎ ‎3‎ ‎…‎ ‎(n－2)‎ ‎3．扇形与弧的定义及区别 ‎(1)弧：圆上两点之间部分叫弧．‎ ‎(2)扇形：由一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形．‎ 图1—42‎ ‎(3)扇形与弧的区别 弧是一段曲线，而扇形是一个面．‎ ‎4．欧拉公式 若有正多面体，f表示它的面数，v表示顶点数，e表示棱数，则有f＋v－e＝2‎ 注意：正多面体只有5种：正四面体、正六面体(正方体)、正八面体、正十二面体、正二十面体．‎ ‎【学习方法指导】‎ ‎［例1］从一个多边形的顶点出发，连接这个顶点与其余的顶点，得到分割成的十个三角形，则这个多边形是_______边形．‎ 点拨：任何一个n(n≥3)边形，按这种方式分割，都会得到(n－2)个三角形．而现在有十个三角形．所以n－2＝10,解出n即可．‎ 解答：十二［例2］如图，你能数出多少个不同的三角形、梯形？这幅图看起来像什么？‎ 2‎ ‎ ‎ 图1—43‎ 点拨：数三角形或梯形的时候，从上至下一层层地数，不要遗漏．‎ 解：三角形有45个，梯形有10个，这幅图象是电线支架．‎ ‎【拓展训练】‎ ‎1．正四面体、正八面体、正二十面体都是由正三角形围成，正六面体是由正方形围成的，正二十面体是由正五边形围成．‎ 正三角形、正方形、正五边形如图1—44所示：‎ 图1—44‎ 2‎