- 2021-04-12 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北省卓越联盟2017-2018学年高二下学期第一次月考数学(文)试题(PDF版)
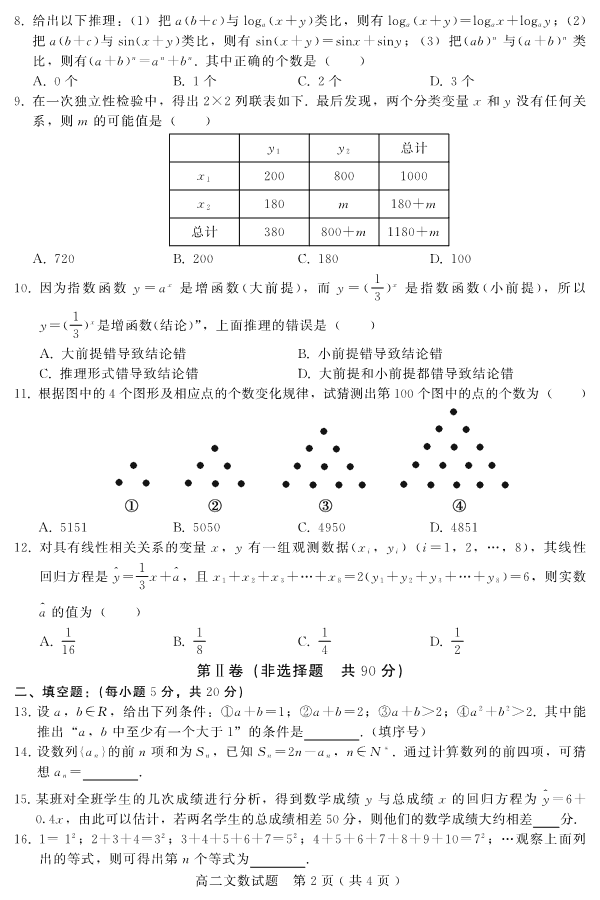
卓越联盟 2017~2018 学年第二学期第一次月考 高二文科数学试题 考试范围:选修 1-2 的 1ư1-2ư2 说明: 1. 本试卷共 4 页,考试时间 120 分钟,满分 150 分. 2. 请将所有答案填写在答题卡上,答在试卷上无效. 第 Ⅰ 卷 (选择题 共 60 分) 一、选择题:(每小题 5 分,共 60 分) 1.在一组样本数据(x1,y1),(x2,y2),ƺ,(xn ,yn )(n≥2,x1,x2,ƺ,xn 不全相等)的散 点图中,若所有样本点(xi,yi)(i=1,2,ƺ,n)都在直线y=1 2 x+1 上,则这组样本数 据的样本相关系数为 ( ) A.-1 B.0 C.1 2 D.1 2.在对两个变量x,y 进行线性回归分析时,有下列步骤:① 对所求出的回归直线方程作出 解释;② 收集数据(xi,yi),i=1,2,ƺ,n;③ 求线性回归方程;④ 求相关系数;⑤ 根 据所搜集的数据绘制散点图.如果根据可行性要求能够作出变量x,y 具有线性相关结论, 则在下列操作中正确的顺序是 ( ) A.①②⑤③④ B.③②④⑤① C.②④③①⑤ D.②⑤④③① 3.用反证法证明:“三角形的内角中至少有一个不大于 60 度”时,反设正确的是 ( ) A. 假设三内角都不大于 60 度 B. 假设三内角都大于 60 度 C. 假设三内角至多有一个大于 60 度 D. 假设三内角至多有两个大于 60 度 4.对于回归方程y^=2-3x,若变量x 增加一个单位,则 ( ) A.y 平均增加 3 个单位 B.y 平均增加 2 个单位 C.y 平均减少 3 个单位 D.y 平均减少 2 个单位 5.在两个变量y 与x 的回归模型中,分别选择了 4 个不同模型,它们的相关指数 R2 如下,其中拟和效果最好的模型是 ( ) A. 模型 4 的相关指数R2 为 0ư98 B. 模型 2 的相关指数R2 为 0ư50 C. 模型 3 的相关指数R2 为 0ư80 D. 模型 1 的相关指数R2 为 0ư25 6.观察式子:1+1 2 2 <3 2,1+1 2 2 +1 3 2 <5 3,1+1 2 2 +1 3 2 +1 4 2 <7 4,ƺ,则由此可以归纳出的式 子为 ( ) A.1+1 2 2 +1 3 2 +ƺ+1n2< 1 2n-1 B.1+1 2 2 +1 3 2 +ƺ+1n2< 1 2n+1 C.1+1 2 2 +1 3 2 +ƺ+1n2<2n-1n D.1+1 2 2 +1 3 2 +ƺ+1n2< 2n 2n+1 7.观察下列等高条形图,其中两个分类变量关系最强的是 ( ) )页 4 共(页 1 第 题试数文二高 8.给出以下推理:(1)把a(b+c)与 loga (x+y)类比,则有 loga (x+y)=logax+logay;(2) 把a(b+c)与 sin(x+y)类比,则有 sin(x+y)=sinx+siny; (3)把(ab) n 与(a+b) n 类 比,则有(a+b) n =an +bn .其中正确的个数是 ( ) A.0 个 B.1 个 C.2 个 D.3 个 9.在一次独立性检验中,得出 2×2 列联表如下.最后发现,两个分类变量x 和y 没有任何关 系,则 m 的可能值是 ( ) y1 y2 总计 x1 200 800 1000 x2 180 m 180+m 总计 380 800+m 1180+m A.720 B.200 C.180 D.100 10.因为指 数 函 数 y=ax 是 增 函 数 (大 前 提),而 y= (1 3) x 是 指 数 函 数 (小 前 提),所 以 y=(1 3) x 是增函数(结论)”,上面推理的错误是 ( ) A. 大前提错导致结论错 B. 小前提错导致结论错 C. 推理形式错导致结论错 D. 大前提和小前提都错导致结论错 11.根据图中的 4 个图形及相应点的个数变化规律,试猜测出第 100 个图中的点的个数为 ( ) A.5151 B.5050 C.4950 D.4851 12.对具有线性相关关系的变量x,y 有一组观测数据(xi,yi)(i=1,2,ƺ,8),其线性 回归方程是y^=1 3 x+a^,且x1+x2+x3+ƺ+x8=2(y1+y2+y3+ƺ+y8)=6,则实数 a^ 的值为 ( ) A.1 16 B.1 8 C.1 4 D.1 2第 Ⅱ 卷 (非选择题 共 90 分) 二、填空题:(每小题 5 分,共 20 分) 13.设a,b∈R,给出下列条件:①a+b=1;②a+b=2;③a+b>2;④a2 +b2 >2.其中能 推出 “a,b 中至少有一个大于 1”的条件是 .(填序号) 14.设数列{an }的前n 项和为Sn ,已知Sn =2n-an ,n∈N ∗ .通过计算数列的前四项,可猜 想an = . 15.某班对全班学生的几次成绩进行分析,得到数学成绩y 与总成绩x 的回归方程为y^=6+ 0ư4x,由此可以估计,若两名学生的总成绩相差 50 分,则他们的数学成绩大约相差 分. 16.1= 1 2;2+3+4=3 2;3+4+5+6+7=5 2;4+5+6+7+8+9+10=7 2;ƺ观察上面列 出的等式,则可得出第n 个等式为 . )页 4 共(页 2 第 题试数文二高 三、解答题:(本大题共 6 小题,共 70 分) 17.(本小题满分 10 分)请用适当的方法证明下列命题: (Ⅰ)求证: 6-2 2> 5- 7; (Ⅱ)已知x∈R,a=x2 -1,b=4x+5,求证:a,b 中至少有一个不小于 0. 18.某市春节期间 7 家超市的广告费用支出xi(万元)和销售额yi(万元)数据如下: 超市 A B C D E F G 广告费支出xi 1 2 4 6 11 13 19 销售额yi 19 32 40 44 52 53 54 (Ⅰ)若用线性回归模型拟合y 与x 的关系,求y 关于x 的线性回归方程; (Ⅱ)用二次函数回归模型拟合y 与x 的关系,可得回归方程:y^=-0ư17x2 +5x+20, 经计算二次函数回归模型和线性回归模型的 R2 分别约为 0ư93 和 0ư75,请用 R2 说 明选择哪个回归模型更合适,并用此模型预测 A 超市广告费用支出为 3 万元时的销 售额. 参考数据及公式:x=8,y=42,∑ 7 i=1 xiyi=2794,∑ 7 i=1 x2i =708, b^= ∑ n i=1 xiyi-nxy ∑ n i=1 x2i -nx2 ,a^=y-b^x. 19.(本小题满分 12 分)某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中 生中随机地抽取了 90 名学生调查,得到了如下列联表: 喜欢数学 不喜欢数学 总计 男 30 ① 45 女 ② 25 45 总计 ③ ④ 90 (Ⅰ)求 ①②③④ 处分别对应的值; (Ⅱ)根据列联表数据,能有多大把握认为 “高中生的性别与喜欢数学”有关? 附: P(K2 ≥k0) 0ư15 0ư10 0ư05 0ư025 0ư010 0ư005 0ư001 k0 2ư072 2ư706 3ư841 5ư024 6ư635 7ư879 10ư828 K2 = n(ad-bc)2 (a+b)(c+d)(a+c)(b+d) . )页 4 共(页 3 第 题试数文二高 20.(本小题满分 12 分)某地区某农产品近几年的产量统计如下表: 年份 2012 2013 2014 2015 2016 2017 年份代码t 1 2 3 4 5 6 年产量y(万吨) 6ư6 6ư7 7 7ư1 7ư2 7ư4 (Ⅰ)根据表中数据,建立y 关于x 的线性回归方程y^=b^t+a^; (Ⅱ)若近几年该农产品每千克的价格v (单位:元)与年产量y 满足的函数关系式为 v=4ư5-0ư3y,且每年该农产品都能售完. ① 根据 (Ⅰ)中所建立的回归方程预测该地区 2018(t=7)年该农产品的产量; ② 当t(1≤t≤7)为何值时,销售额S 最大? 附:对于一组数据(t1,y1),(t2,y2),ƺ,(tn ,yn )其回归直线y^=b^t+a^ 的斜率 和截距的最小二乘估计分别为:b^= ∑ n i=1(ti-t)(yi-y) ∑ n i=1(ti-t)2 ,a^=y-b^t. 21.(本小题满分 12 分)已知f(x)=3-x2 1+x2 . (Ⅰ)计算f(3),f(4),f(1 3)及f(1 4)的值; (Ⅱ)由 (1)的结果猜想一个普遍的结论,并加以证明; (Ⅲ)求值:f(1)+f(2)+ƺ+f(2018)+f(1 2)+f(1 3)+ƺ +f(1 2018). 22.(本小题满分 12 分) (Ⅰ)已知a>0,b>0,c>0,且a+b+c=1,求证:a2 +b2 +c2 ≥1 3; (Ⅱ)已知a>0,b>0,且a+b=1,求证:(a+1a )(b+1b )≥25 4 . )页 4 共(页 4 第 题试数文二高查看更多