【数学】2019届一轮复习人教A版 二次函数与幂函数 学案
第7讲 二次函数与幂函数
考纲要求
考情分析
命题趋势
1.掌握二次函数的图象与性质,会求二次函数的最值(值域)、单调区间.
2.了解幂函数的概念.
3.结合函数y=x,y=x2,y=x3,y=,y=x的图象,了解它们的变化情况.
2017·全国卷Ⅲ,11
2017·山东卷,10
2016·全国卷Ⅲ,6
2015·浙江卷,18
1.二次函数的图象和性质,经常与其他知识综合考查.
2.幂函数的图象和性质,很少单独出题.
3.二次函数的综合应用,经常与导数、不等式综合考查.
分值:5~8分
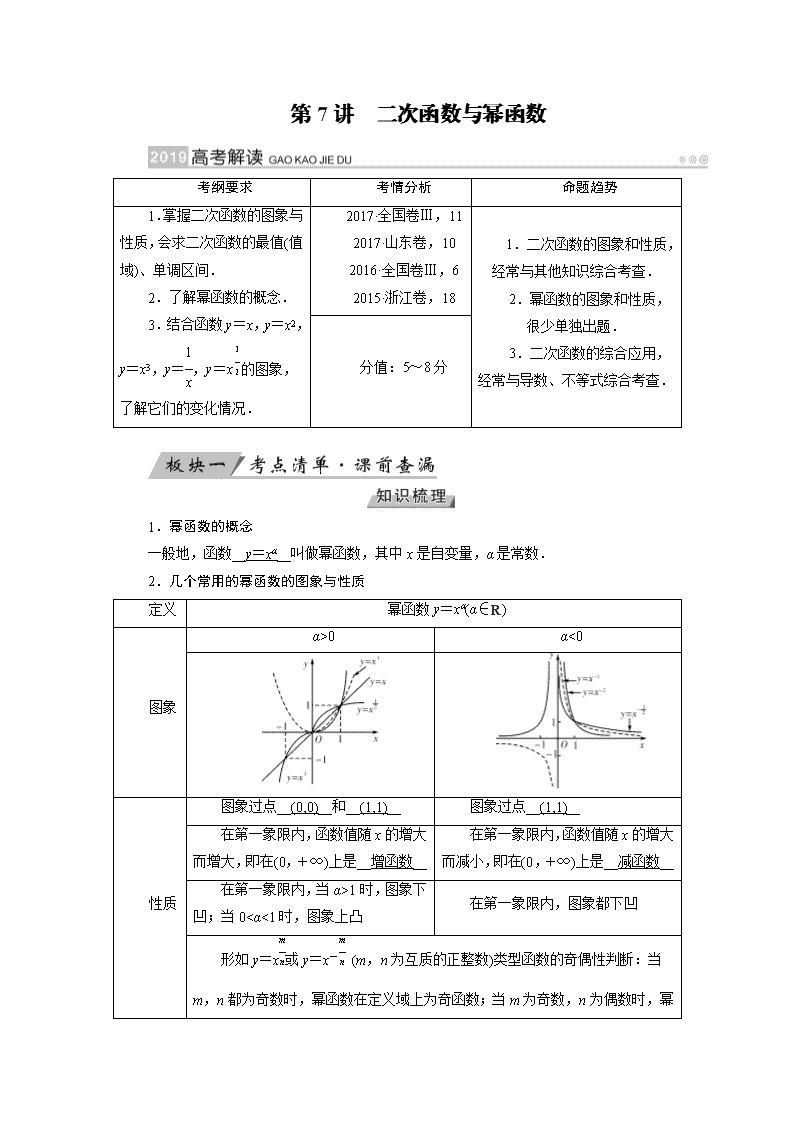
1.幂函数的概念
一般地,函数__y=xα__叫做幂函数,其中x是自变量,α是常数.
2.几个常用的幂函数的图象与性质
定义
幂函数y=xα(α∈R)
图象
α>0
α<0
性质
图象过点__(0,0)__和__(1,1)__
图象过点__(1,1)__
在第一象限内,函数值随x的增大而增大,即在(0,+∞)上是__增函数__
在第一象限内,函数值随x的增大而减小,即在(0,+∞)上是__减函数__
在第一象限内,当α>1时,图象下凹;当0<α<1时,图象上凸
在第一象限内,图象都下凹
形如y=x或y=x- (m,n为互质的正整数)类型函数的奇偶性判断:当m,n都为奇数时,幂函数在定义域上为奇函数;当m为奇数,n为偶数时,幂函数在定义域上为非奇非偶函数;当m为偶数,n
为奇数时,幂函数在定义域上为偶函数
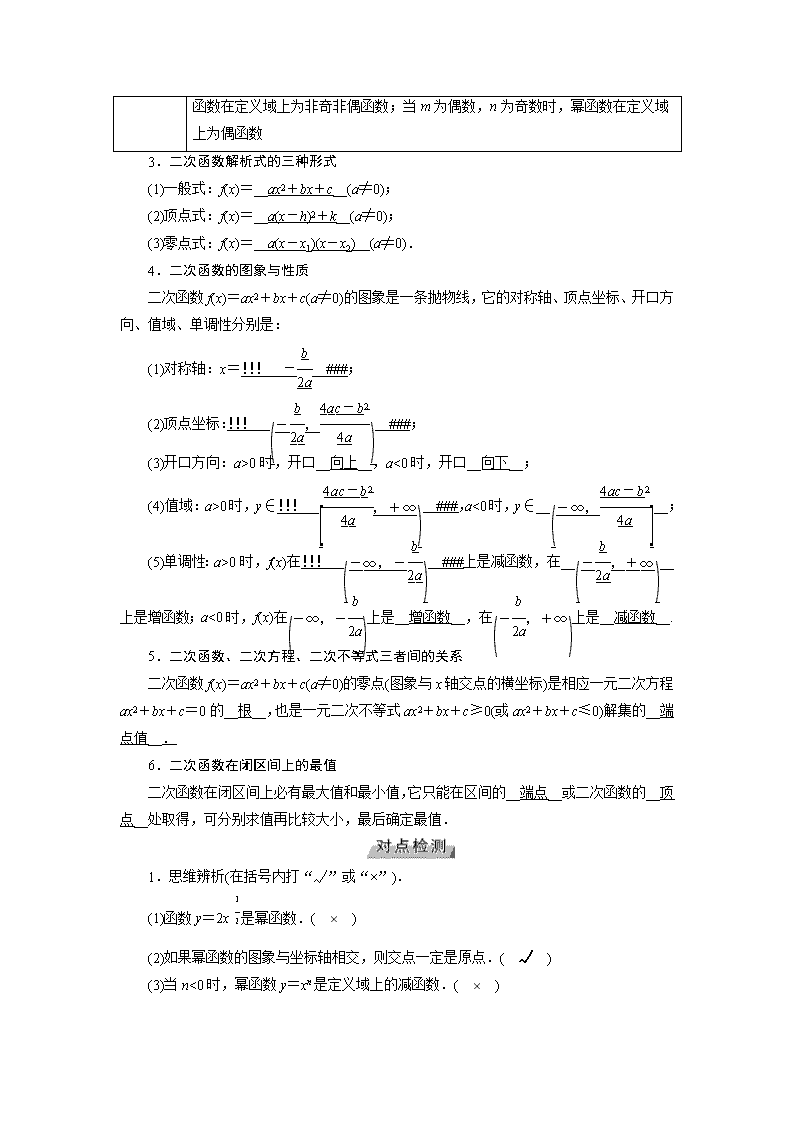
3.二次函数解析式的三种形式
(1)一般式:f(x)=__ax2+bx+c__(a≠0);
(2)顶点式:f(x)=__a(x-h)2+k__(a≠0);
(3)零点式:f(x)=__a(x-x1)(x-x2)__(a≠0).
4.二次函数的图象与性质
二次函数f(x)=ax2+bx+c(a≠0)的图象是一条抛物线,它的对称轴、顶点坐标、开口方向、值域、单调性分别是:
(1)对称轴:x=!!! - ###;
(2)顶点坐标:!!! ###;
(3)开口方向:a>0时,开口__向上__,a<0时,开口__向下__;
(4)值域:a>0时,y∈!!! ###,a<0时,y∈____;
(5)单调性:a>0时,f(x)在!!! ###上是减函数,在____上是增函数;a<0时,f(x)在上是__增函数__,在上是__减函数__.
5.二次函数、二次方程、二次不等式三者间的关系
二次函数f(x)=ax2+bx+c(a≠0)的零点(图象与x轴交点的横坐标)是相应一元二次方程ax2+bx+c=0的__根__,也是一元二次不等式ax2+bx+c≥0(或ax2+bx+c≤0)解集的__端点值__.
6.二次函数在闭区间上的最值
二次函数在闭区间上必有最大值和最小值,它只能在区间的__端点__或二次函数的__顶点__处取得,可分别求值再比较大小,最后确定最值.
1.思维辨析(在括号内打“√”或“×”).
(1)函数y=2x是幂函数.( × )
(2)如果幂函数的图象与坐标轴相交,则交点一定是原点.( √ )
(3)当n<0时,幂函数y=xn是定义域上的减函数.( × )
(4)二次函数y=ax2+bx+c,x∈[m,n]的最值一定是.( × )
解析 (1)错误.不符合幂函数的定义.
(2)正确.因为图象与坐标轴相交,则由x=0得y=0,若y=0,则得x=0.
(3)错误.幂函数y=x-1在定义域上不单调.
(4)错误.当-∉[m,n]时,二次函数的最值,在区间端点取得,而非.
2.函数y=x的图象(图中虚线为直线y=x)是( B )
解析 因为函数y=x是幂函数,幂函数在第一象限内恒过点(1,1),排除A项,D项;当x>1,0
0时图象经过点(0,0)和点(1,1),在第一象限的部分“上升”;α<0时图象不过点(0,0),经过点(1,1),在第一象限的部分“下降”;
(2)曲线在第一象限的“凹凸性”:α>1时曲线下凹,0<α<1时曲线上凸,α<0时曲线下凹;
(3)函数的奇偶性:一般先将函数式化为正指数幂或根式形式,再根据函数的定义域和奇偶性定义判断其奇偶性.
【例1】 (1)已知函数f(x)=(m2-m-1)xm2+m-3是幂函数,且x∈(0,+∞)时,f(x)是增函数,则m的值为( B )
A.-1 B.2
C.-1或2 D.3
(2)幂函数y=f(x)的图象过点(4,2),则幂函数y=f(x)的图象是( C )
(3)已知f(x)=x,若00,∴m=2.
(2)∵幂函数y=f(x)的图象过点(4,2),∴f(x)=x.
(3)∵0-2x的解集为(1,3).若方程f(x)+6a=0有两个相等的根,则f(x)的单调递增区间为__(-∞,-3]__.
解析 (1)设f(x)=ax2+bx+c(a≠0).
由题意得解得
所以所求二次函数为f(x)=-4x2+4x+7.
(2)因为f(x)+2x>0的解集为(1,3),
设f(x)+2x=a(x-1)(x-3),且a<0,
所以f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a.①
由方程f(x)+6a=0,得ax2-(2+4a)x+9a=0.②
因为方程②有两个相等的根,
所以Δ=[-(2+4a)]2-4a·9a=0,解得a=1或a=-.
由于a<0,舍去a=1.将a=-代入①式得
f(x)=-x2-x-=-(x+3)2+,
所以函数f(x)的单调递增区间是(-∞,-3].
三 二次函数的图象和性质
二次函数在闭区间上的最大值和最小值可能在三个地方取到:区间的两个端点处,或对称轴处.也可以作出二次函数在该区间上的图象,由图象来判断最值.解题的关键是讨论对称轴与所给区间的相对位置关系.
【例3】 (1)已知二次函数f(x)=ax2-2x(0≤x≤1),求f(x)的最小值.
(2)已知a是实数,记函数f(x)=x2-2x+2在[a,a+1]上的最小值为g(a),求g(a)的解析式.
解析 (1)①当a>0时,f(x)=ax2-2x图象的开口方向向上,且对称轴为x=.
当≤1,即a≥1时,f(x)=ax2-2x图象的对称轴在[0,1]内,
∴f(x)在上递减,在上递增.
∴f(x)min=f=-=-.
当>1,即01时,函数图象如图(3),函数f(x)在区间[a,a+1]上为增函数,所以最小值为f(a)=a2-2a+2.
综上可知,g(a)=
【例4】 (1)若函数f(x)=x2+2ax+3在区间[-4,6]上是单调函数,则实数a的取值范围为__(-∞,-6]∪[4,+∞)__.
(2)若函数f(x)=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是!!! ###.
解析 (1)由于函数f(x)的图象开口向上,对称轴是x=-a,所以要使f(x)在[-4,6]上是单调函数,应有-a≤-4或-a≥6,即a≤-6或a≥4.
(2)函数f(x)图象的对称轴为x=,且f=-,f(3)=f(0)=-4,由二次函数的图象知m的取值范围为.
1.若幂函数f(x)=mxα的图象经过点A,则它在点A处的切线方程是( C )
A.2x-y=0 B.2x+y=0
C.4x-4y+1=0 D.4x+4y+1=0
解析 根据函数f(x)=mxα为幂函数,所以m=1,根据图象经过点A,则有α=
eq f(1,2),所以f(x)=x,f′(x)=,f′=1,故所求切线方程是4x-4y+1=0.
2.已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( B )
A.[2-,2+] B.(2-,2+)
C.[1,3] D.(1,3)
解析 由题意可知,f(x)=ex-1>-1,g(x)=-x2+4x-3=-(x-2)2+1≤1.若有f(a)=g(b),则g(b)∈(-1,1],
即-b2+4b-3>-1,解得2-2x+m在[-1,1]上恒成立.
即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)=x2-3x+1-m,因为g(x)的图象开口向上,对称轴为x=,所以g(x)在[-1,1]上是减函数,
故g(x)min=g(1)=12-3×1+1-m>0,解得m<-1.
故实数m的取值范围为(-∞,-1).
易错点 忽视一元二次方程中对Δ的讨论
错因分析:忽略已知一元二次方程有根时,便隐含了Δ≥0以及韦达定理的内容.
【例1】 已知关于x的方程x2-2mx+4m2-6=0的两根为α,β,试求(α-1)2+(β-1)2的最小值.
解析 由题意得
∴(α-1)2+(β-1)2=(α+β)2-2αβ-2(α+β)+2=(2m)2-2(4m2-6)-4m+2=-4m2-4m+14=-42+15,
又∵Δ≥0,即(-2m)2-4(4m2-6)≥0,∴-≤m≤,
∴当m=时,(α-1)2+(β-1)2的最小值为6-4.
【跟踪训练1】 已知函数f(x)=x2+2mx+2m+3(m∈R),若关于x的方程f(x)=0有实数根,且两根分别为x1,x2,则(x1+x2)·x1x2的最大值为( B )
A.1 B.2
C.3 D.4
解析 ∵x1+x2=-2m,x1x2=2m+3,
∴(x1+x2)·x1x2=-2m(2m+3)=-42+.
又Δ=4m2-4(2m+3)≥0,∴m≤-1或m≥3.
∵t=-42+在m∈(-∞,-1)上单调递增,在m∈[3,+∞)上单调递减,m=-1时最大值为2.
∴(x1+x2)·x1x2的最大值为2,故选B.
课时达标 第7讲
[解密考纲]本考点考查幂函数的图象与性质、二次函数的单调性与最值、二次函数恒成立问题以及二次方程的根的分布问题,一般以选择题、填空题的形式呈现,排在中间靠前的位置,难度中等.
一、选择题
1.(2018·河南南阳模拟)已知幂函数f(x)=k·xa的图象过点,则k+a=( C )
A. B.1
C. D.2
解析 因为f(x)=k·xa是幂函数,所以k=1.又f(x)的图象过点,所以a=,所以a=,所以k+a=1+=.
2.(2018·天津模拟)抛物线y=ax2+bx+c的顶点在第一象限与x轴的两个交点分别位于原点两侧,则a,b,c的符号为( B )
A.a<0,b<0,c<0 B.a<0,b>0,c>0
C.a<0,b<0,c>0 D.a<0,b>0,c<0
解析 由题意知,抛物线开口向下,故a<0.由抛物线与x轴的两个交点分别位于原点两侧,得ac<0,所以c>0.再由顶点在第一象限得->0,所以b>0.
3.对任意的x∈[-2,1],不等式x2+2x-a≤0恒成立,则实数a的取值范围是( D )
A.(-∞,0] B.(-∞,3]
C.[0,+∞) D.[3,+∞)
解析 设f(x)=x2+2x-a(x∈[-2,1]),由二次函数的图象知,当x=1时,f(x)取得最大值3-a,所以3-a≤0,解得a≥3,故选D.
4.对于幂函数f(x)=x,若0
C.f= D.无法确定
解析 根据幂函数的性质:当00),已知f(m)<0,则( C )
A.f(m+1)≥0 B.f(m+1)≤0
C.f(m+1)>0 D.f(m+1)<0
解析 因为f(x)的对称轴为x=-,f(0)=a>0,所以f(x)的大致图象如图所示.
由f(m)<0,得-10,所以f(m+1)>f(0)>0,故选C.
6.(2017·山东卷)已知当x∈[0,1]时,函数y=(mx-1)2的图象与y=+m的图象有且只有一个交点,则正实数m的取值范围是( B )
A.(0,1]∪[2,+∞) B.(0,1]∪[3,+∞)
C.(0,]∪[2,+∞) D.(0,]∪[3,+∞)
解析 在同一直角坐标系中,分别作出函数f(x)=(mx-1)2=
m22与g(x)=+m的大致图象.
分两种情形:
(1)当01时,0<<1,如图②,要使f(x)与g(x)的图象在[0,1]上只有一个交点,只需g(1)≤f(1),即1+m≤(m-1)2,解得m≥3或m≤0(舍去).
综上所述,m∈(0,1]∪[3,+∞).
故选B.
二、填空题
7.已知函数f(x)=x,且f(2x-1)0时,f(x)在[2,3]上为增函数,
故⇒⇒
当a<0时,f(x)在[2,3]上为减函数,
故⇒⇒
∴或
(2)∵b<1,∴a=1,b=0,即f(x)=x2-2x+2.
g(x)=x2-2x+2-mx=x2-(2+m)x+2,
∵g(x)在[2,4]上单调,∴≤2或≥4.
∴m≤2或m≥6.故m的取值范围为(-∞,2]∪[6,+∞).
12.(2018·河北唐山调研)设a为实数,函数f(x)=x2+|x-a|+1,x∈R.求f(x)的最小值.
解析 (1)①当x≤a时,函数f(x)=x2-x+a+1=2+a+.
若a≤,则函数f(x)在(-∞,a]上单调递减,从而函数f(x)在(-∞,a]上的最小值为f(a)=a2+1;
若a>,则函数f(x)在(-∞,a]上的最小值为f=+a,且f≤f(a).
②当x≥a时,函数f(x)=x2+x-a+1=2-a+.
若a≤-,则函数f(x)在[a,+∞)上的最小值为f=-a,且f≤f(a);
若a>-,则函数f(x)在[a,+∞)上单调递增,从而函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
综上,f(x)min=