- 2021-04-12 发布 |
- 37.5 KB |
- 3页


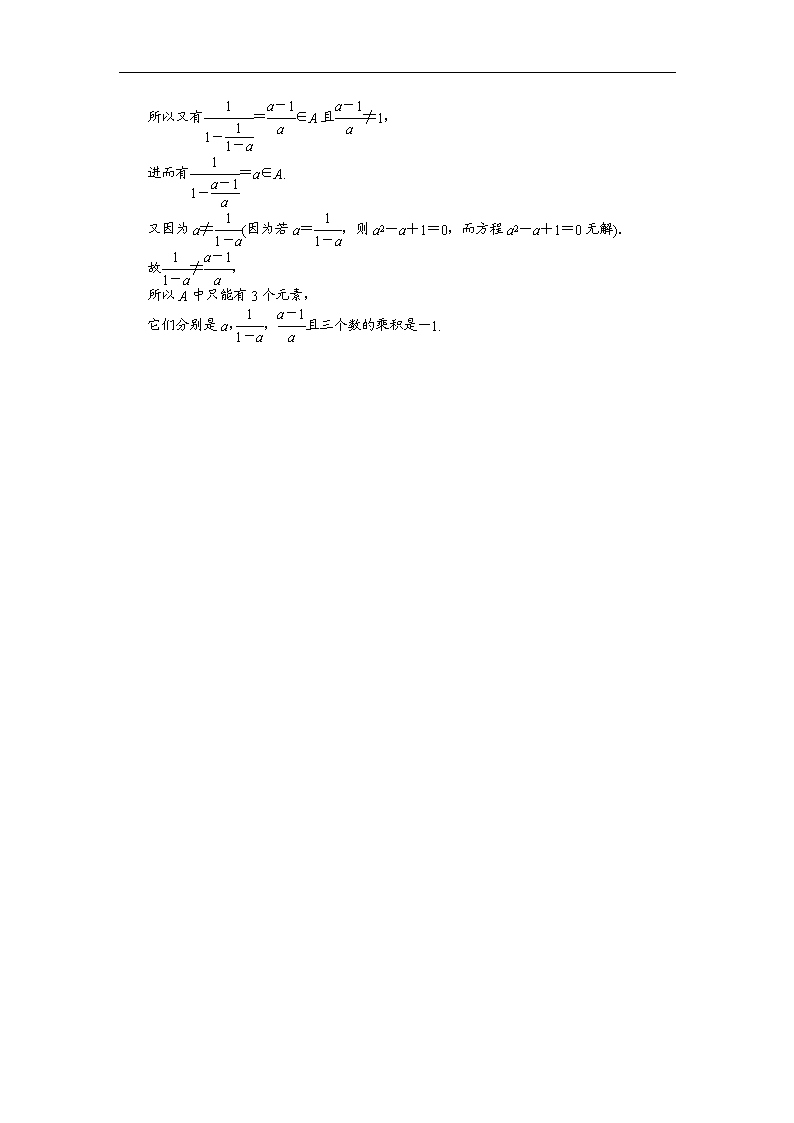
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学人教A版必修一教学训练(教师版)1_1_1_1
(本栏目内容,在学生用书中以活页形式分册装订!) 一、选择题(每小题5分,共20分) 1.考察下列每组对象,能构成一个集合的是( ) ①某校高一年级成绩优秀的同学; ②直角坐标系中横、纵坐标相等的点; ③不小于3的自然数; ④2008年北京奥运会比赛金牌获得者. A.③④ B.②③④ C.②③ D.②④ 解析: ①中“成绩优秀”没有明确的标准,所以不能构成一个集合.②③④中的对象都满足确定性与整体性,所以能构成集合. 答案: B 2.由a,a,b,b,a2,b2构成集合A,则集合A中的元素最多有( ) A.6个 B.5个 C.4个 D.3个 解析: 根据集合中元素的互异性可知,集合A中的元素最多有4个,故选C. 答案: C[来源:学科网ZXXK] 3.已知集合A是由0,m,m2-3m+2三个元素组成的集合,且2∈A,则实数m的值为( ) A.2 B.3 C.0或3 D.0,2,3均可[来源:学科网] 解析: 因为2∈A,所以m=2或m2-3m+2=2,解得m=0或m=2或m=3.又集合中的元素要满足互异性,对m的所有取值进行一一验证可得m=3,故选B. 答案: B 4.已知集合A由x<1的数构成,则有( ) A.3∈A B.1∈A C.0∈A D.-1∉A 解析: 很明显3,1不满足不等式,而0,-1满足不等式. 答案: C 二、填空题(每小题5分,共10分) 5.已知集合A由元素1和a2构成,实数a不能取的值的集合是________. 解析: 由互异性知a2≠1,即a≠±1, 故实数a不能取的值的集合是{1,-1}. 答案: {1,-1} 6.如果具有下述性质的x都是集合M中的元素,其中:x=a+b(a,b∈Q),则下列元素中不属于集合M的元素个数是______个. ①x=0,②x=,③x=3-2π, ④x=,⑤x=+. 解析: ①当a=b=0时,x=0;①正确; ②当a=0,b=1时,x=,②正确;[来源:Zxxk.Com] ③当a=3,b=-2π时,b∉Q,x=3-2π∉M,③不正确; ④当x=3,b=2时,x=3+2=,④正确; ⑤x=+=2-+2+=4 当a=4,b=0时,x=4,⑤正确. 答案: 1[来源:学|科|网] 三、解答题(每小题10分,共20分) 7.已知集合A由元素a-3,2a-1,a2-4构成,且-3∈A,求实数a的值. 解析: ∵-3∈A,A={a-3,2a-1,a2-4}, ∴a-3=-3或2a-1=-3或a2-4=-3. 若a-3=-3, 则a=0,此时集合A={-3,-1,-4},符合题意. 若2a-1=-3,则a=-1,此时集合A={-4,-3,-3}, 不满足集合中元素的互异性. 若a2-4=-3,则a=1或a=-1(舍去), 当a=1时,集合A={-2,1,-3},符合题意. 综上可知,a=0,或a=1. 8.已知集合M中含有三个元素2,a,b,集合N中含有三个元素2a,2,b2,且M=N,求a,b的值. 解析: 方法一:根据集合中元素的互异性, 有或, 解得或或. 再根据集合中元素的互异性,得或. 方法二:∵两个集合相同,则其中的对应元素相同. ∴,[来源:学_科_网Z_X_X_K] 即 ∵集合中的元素互异,∴a,b不能同时为零. 当b≠0时,由②得a=0,或b=. 当a=0时,由①得b=1,或b=0(舍去). 当b=时,由①得a=. 当b=0时,a=0(舍去). ∴或 ☆☆☆ 9.(10分)数集A满足条件:若a∈A,则∈A(a≠1). (1)若2∈A,试求出A中其他所有元素; (2)自己设计一个数属于A,然后求出A中其他所有元素; (3)从上面的解答过程中,你能悟出什么道理?并大胆证明你发现的“道理”. 解析: (1)2∈A,则∈A, 即-1∈A,则∈A,即∈A,则∈A, 即2∈A,所以A中其他所有元素为-1,. (2)如:若3∈A,则A中其他所有元素为-,. (3)分析以上结果可以得出:A中只能有3个元素,它们分别是a,,, 且三个数的乘积为-1. 证明如下:若a∈A,a≠1,则有∈A且≠1, 所以又有=∈A且≠1, 进而有=a∈A. 又因为a≠(因为若a=,则a2-a+1=0,而方程a2-a+1=0无解). 故≠, 所以A中只能有3个元素, 它们分别是a,,且三个数的乘积是-1.查看更多