- 2021-04-12 发布 |
- 37.5 KB |
- 11页
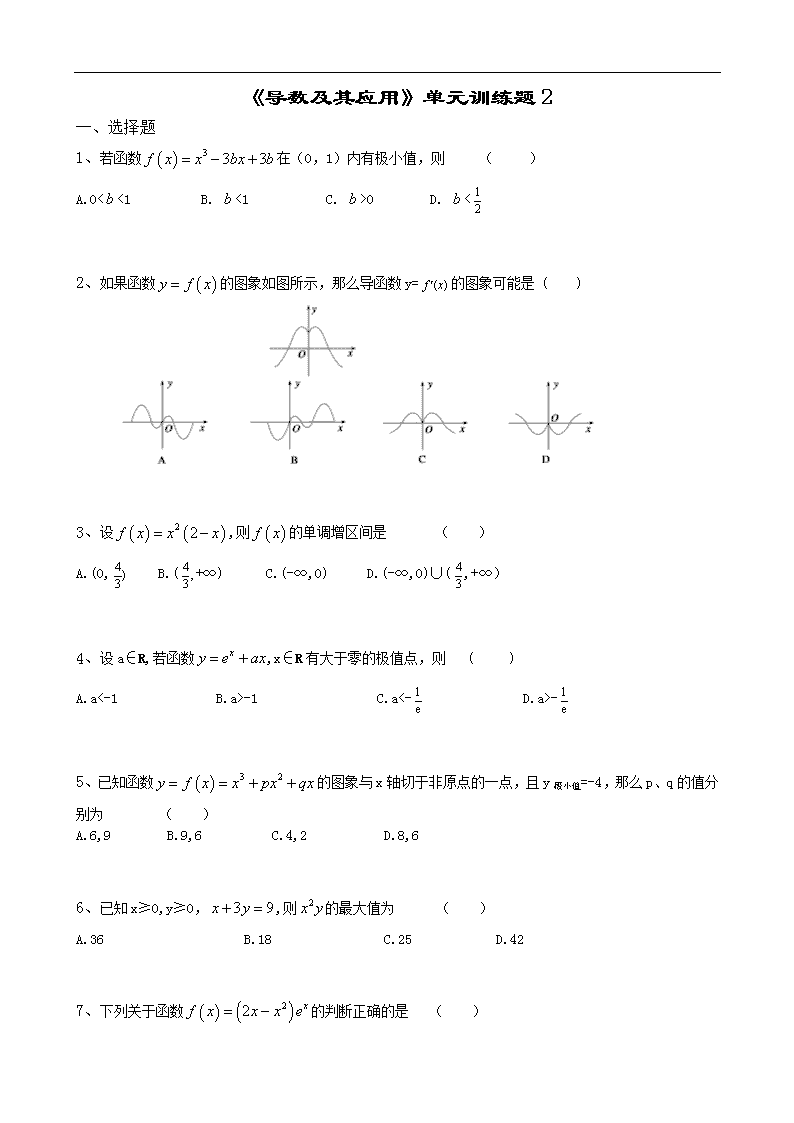

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:《导数及其应用》单元训练题2
《导数及其应用》单元训练题2 一、选择题 1、若函数在(0,1)内有极小值,则 ( ) A.0<<1 B. <1 C. >0 D. < 2、如果函数的图象如图所示,那么导函数y=的图象可能是 ( ) 3、设,则的单调增区间是 ( ) A.(0, B.(+∞) C.(-∞,0) D.(-∞,0)∪(,+∞) 4、设a∈R,若函数,x∈R有大于零的极值点,则 ( ) A.a<-1 B.a>-1 C.a<- D.a>- 5、已知函数的图象与x轴切于非原点的一点,且y极小值=-4,那么p、q的值分别为 ( ) A.6,9 B.9,6 C.4,2 D.8,6 6、已知x≥0,y≥0,,则的最大值为 ( ) A.36 B.18 C.25 D.42 7、下列关于函数的判断正确的是 ( ) ①f(x)>0的解集是{x|0查看更多