2016届高考数学(理)大一轮复习达标训练试题:课时跟踪检测(五十二) 圆的方程
课时跟踪检测(五十二) 圆的方程
一、选择题
1.(2015·北京西城期末)若坐标原点在圆(x-m)2+(y+m)2=4 的内部,则实数 m 的取值
范围是( )
A.(-1,1) B.(- 3, 3)
C.(- 2, 2) D. - 2
2
, 2
2
2.圆 x2+y2-4x-4y-10=0 上的点到直线 x+y-14=0 的最大距离与最小距离的和是
( )
A.30 B.18
C.10 2 D.5 2
3.设圆的方程是 x2+y2+2ax+2y+(a-1)2=0,若 0
0).若
圆 C 上存在点 P,使得 ∠APB=90°,则 m 的最大值为( )
A.7 B.6
C.5 D.4
二、填空题
7.已知圆 C 关于 y 轴对称,经过点(1,0)且被 x 轴分成两段,弧长比为 1∶2,则圆 C 的
方程为 __________________________________________________________________.
8.(2015·绍兴模拟)点 P(1,2)和圆 C:x2+y2+2kx+2y+k2=0 上的点的距离的最小值是
________.
9.若圆 C:x2-2mx+y2-2 my+2=0 与 x 轴有公共点,则 m 的取值范围是________.
10.已知两点 A(-2,0),B(0,2),点 C 是圆 x2+y2-2x=0 上任意一点,则△ABC 面积
的最小值是________.
三、解答题
11.已知圆的方程是 x2+y2-2ax+2(a-2)y+2=0,其中 a≠1,且 a∈R.
(1)求证:a 取不为 1 的实数时,上述圆过定点;
(2)求圆心的轨迹方程.
12. 已知以点 P 为圆心的圆经过点 A(-1,0)和 B(3,4),线段 AB 的垂直平分线交圆 P 于
点 C 和 D,且|CD|=4 10.
(1)求直线 CD 的方程;
(2)求圆 P 的方程.
答案
1.选 C ∵(0,0)在(x-m)2+(y+m)2=4 的内部,则有(0-m)2+(0+m)2<4,解得-
20,即 0+a2+0+12> 2a,所以原点在圆外.
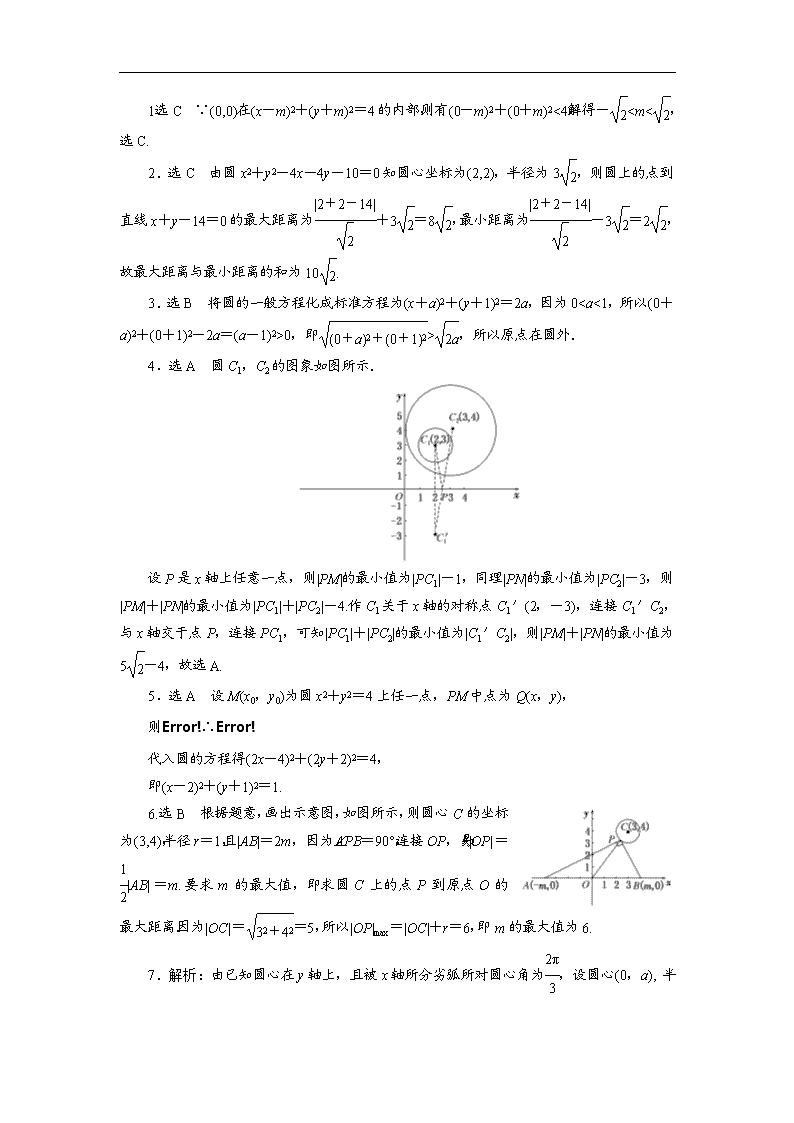
4.选 A 圆 C1,C2 的图象如图所示.
设 P 是 x 轴上任意一点,则|PM|的最小值为|PC1|-1,同理|PN|的最小值为|PC2|-3,则
|PM|+|PN|的最小值为|PC1|+|PC2|-4.作 C1 关于 x 轴的对称点 C1′(2,-3),连接 C1′C2,
与 x 轴交于点 P,连接 PC1,可知|PC1|+|PC2|的最小值为|C1′C2|,则|PM|+|PN|的最小值为
5 2-4,故选 A.
5.选 A 设 M(x0,y0)为圆 x2+y2=4 上任一点,PM 中点为 Q(x,y),
则
x=x0+4
2
,
y=y0-2
2
,
∴ x0=2x-4,
y0=2y+2.
代入圆的方程得(2x-4)2+(2y+2)2=4,
即(x-2)2+(y+1)2=1.
6.选 B 根据题意,画出示意图,如图所示,则圆心 C 的坐
标为(3,4),半径 r=1,且|AB|=2m,因为∠APB=90°,连接 OP,
易知|OP|=1
2|AB|=m.要求 m 的最大值,即求圆 C 上的点 P 到原
点 O 的最大距离.因为|OC|= 32+42=5,所以|OP|max=|OC|+r
=6,即 m 的最大值为 6.
7.解析:由已知圆心在 y 轴上,且被 x 轴所分劣弧所对圆心角为2π
3
,设圆心(0,a), 半
径为 r,则 rsinπ
3
=1,rcosπ
3
=|a|,解得 r= 2
3
,即 r2=4
3
,|a|= 3
3
,
即 a=± 3
3
,故圆 C 的方程为 x2+ y± 3
3 2=4
3.
答案:x2+ y± 3
3 2=4
3
8.解析:圆的方程化为标准式为(x+k)2+(y+1)2=1.
∴圆心 C(-k,-1),半径 r=1.
易知点 P(1,2)在圆外.
∴点 P 到圆心 C 的距离为:
|PC|= k+12+32= k+12+9≥3.
∴|PC|min=3.
∴点 P 和圆 C 上点的最小距离 dmin=|PC|min-r=3-1=2.
答案:2
9 . 解 析 : 圆 C 的 标 准 方 程 为 (x - m)2 + (y - m )2 = m2 + m - 2 , 依 题 意 有
m2+m-2>0,
m≤ m2+m-2,
m≥0.
得 m≥ 2.
答案:[ 2,+∞)
10.解析:lAB:x-y+2=0,圆心(1,0)到 l 的距离 d= 3
2
,
则 AB 边上的高的最小值为 3
2
-1.
故△ABC 面积的最小值是1
2
×2 2×
3
2
-1 =3- 2.
答案:3- 2
11.解:(1)证明:将方程 x2+y2-2ax+2(a-2)y+2=0 整理得 x2+y2-4y+2-a(2x-
2y)=0(a≠1,且 a∈R),
令 x2+y2-4y+2=0,
2x-2y=0,
解得 x=1,
y=1.
所以 a 取不为 1 的实数时,上述圆过定点(1,1).
(2)由题意知圆心坐标为(a,2-a),且 a≠1,
又设圆心坐标为(x,y),则有 x=a,
y=2-a,
消去参数 a,得 x+y-2=0(x≠1),即为所
求圆心的轨迹方程.
12.解:(1)∵直线 AB 的斜率 k=1,AB 的中点坐标为(1,2).
∴直线 CD 的方程为 y-2=-(x-1),即 x+y-3=0.
(2)设圆心 P(a,b),则由 P 在 CD 上得 a+b-3=0. ①
又∵直径|CD|=4 10,∴|PA|=2 10.
∴(a+1)2+b2=40. ②
由①②解得 a=-3,
b=6,
或 a=5,
b=-2.
∴圆心 P(-3,6)或 P(5,-2).
∴圆 P 的方程为(x+3)2+(y-6)2=40 或(x-5)2+(y+2)2=40.