高一数学（人教A版）必修4能力提升：第一章综合检测题

高一数学（人教A版）必修4能力提升：第一章综合检测题

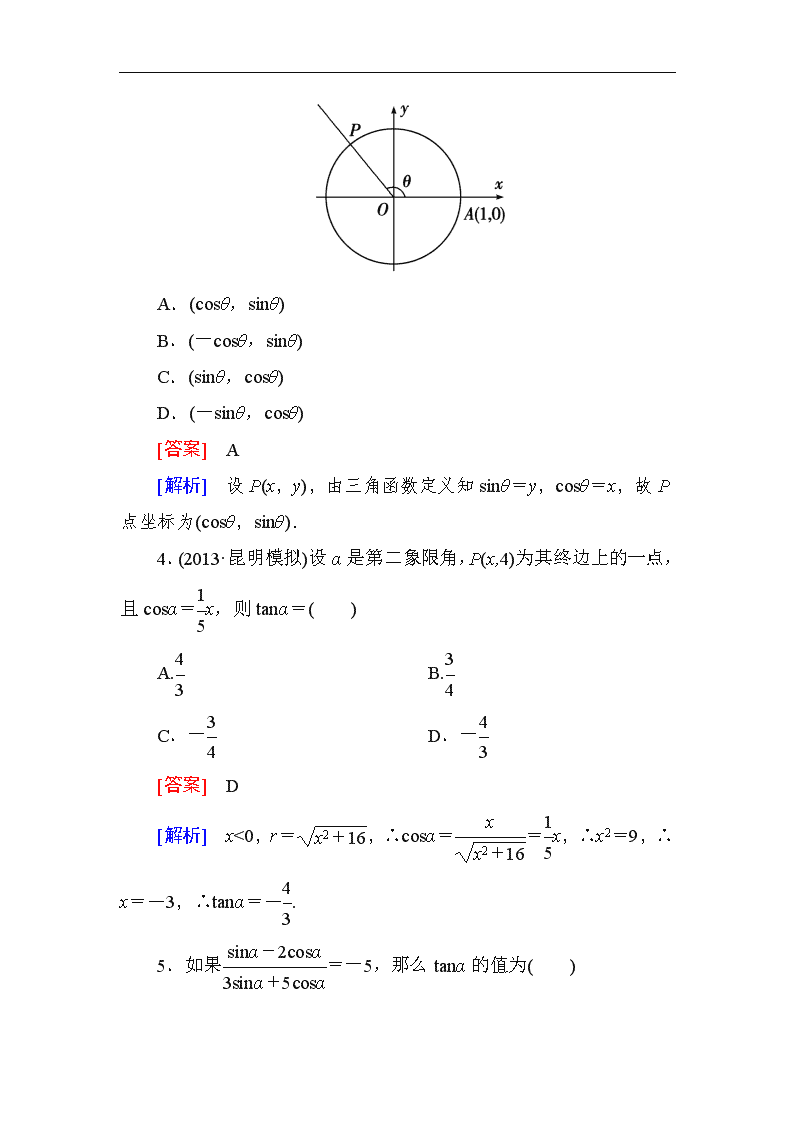
第一章综合检测题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)‎ ‎1．若α是第二象限角，则180°－α是(　　)‎ A．第一象限角　　　　　　 B．第二象限角 C．第三象限角 D．第四象限角 ‎[答案]　A ‎[解析]　α为第二象限角，不妨取α＝120°，则180°－α为第一象限角．‎ ‎2．已知2弧度的圆心角所对的弦长为2，则这个圆心角所对的弧长是(　　)‎ A．2 B．sin2‎ C. D．2sin1‎ ‎[答案]　C ‎[解析]　由题设，圆弧的半径r＝，∴圆心角所对的弧长l＝2r＝.‎ ‎3．(2013·宁波模拟)如图，在直角坐标系xOy中，射线OP交单位圆O于点P，若∠AOP＝θ，则点P的坐标是(　　)‎ A．(cosθ，sinθ)‎ B．(－cosθ，sinθ)‎ C．(sinθ，cosθ)‎ D．(－sinθ，cosθ)‎ ‎[答案]　A ‎[解析]　设P(x，y)，由三角函数定义知sinθ＝y，cosθ＝x，故P点坐标为(cosθ，sinθ)．‎ ‎4．(2013·昆明模拟)设α是第二象限角，P(x,4)为其终边上的一点，且cosα＝x，则tanα＝(　　)‎ A.　　 　 B.　 　　‎ C．－　　　 D．－ ‎[答案]　D ‎[解析]　x<0，r＝，∴cosα＝＝x，∴x2＝9，∴x＝－3，∴tanα＝－.‎ ‎5．如果＝－5，那么tanα的值为(　　)‎ A．－2 B．2 ‎ C. D．－ ‎[答案]　D ‎[解析]　∵sinα－2cosα＝－5(3sinα＋5cosα)，‎ ‎∴16sinα＝－23cosα，∴tan＝－.‎ ‎6．如果sinα＋cosα＝，那么|sin3α－cos3α|的值为(　　)‎ A. B．－ C.或－ D．以上全错 ‎[答案]　C ‎[解析]　由已知，两边平方得sinαcosα＝－.‎ ‎∴|sin3α－cos3α|＝|(sinα－cosα)(sin2α＋cos2α＋sinαcosα)|＝·|1＋sinαcosα|＝.∴sin3α－cos3α＝±.‎ ‎7．(2013·普宁模拟)若＝2，则＋的值为(　　)‎ A．－ B. C. D．－ ‎[答案]　C ‎[解析]　∵＝2，∴sinθ＝3cosθ ‎∴＋＝＋＝ 由得cos2θ＝ ‎∴＋＝.‎ ‎8．若sinα是5x2－7x－6＝0的根，‎ 则＝(　　)‎ A. B. ‎ C. D. ‎[答案]　B ‎[解析]　方程5x2－7x－6＝0的两根为x1＝－，‎ x2＝2.则sinα＝－ 原式＝＝－＝.‎ ‎9．函数y＝sin的一个单调递减区间为(　　)‎ A. B. C. D. ‎[答案]　A ‎[解析]　令＋2kπ≤2x＋≤＋2kπ(k∈Z)，整理得＋kπ≤x≤＋kπ，所以仅有是单调递减区间．‎ ‎10．将函数y＝sin(x－)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再将所得的图象向右平移个单位，得到的图象对应的解析式是(　　)‎ A．y＝sinx B．y＝sin(x－)‎ C．y＝sin(x－) D．y＝sin(2x－)‎ ‎[答案]　B ‎[解析]　‎ ‎11．已知函数f(x)＝sin(x∈R)，下面结论错误的是(　　)‎ A．函数f(x)的最小正周期为2π B．函数f(x)在区间上是增函数 C．函数f(x)的图象关于直线x＝0对称 D．函数f(x)是奇函数 ‎[答案]　D ‎[解析]　∵f(x)＝sin＝－cosx(x∈R)，‎ ‎∴T＝2π，在上是增函数．‎ ‎∵f(－x)＝－cos(－x)＝－cosx＝f(x)．‎ ‎∴函数f(x)是偶函数，图象关于y轴即直线x＝0对称．‎ ‎12．已知某帆船中心比赛场馆区的海面上每天海浪高度y(米)可看作是时间t(0≤t≤24，单位：小时)的函数，记作y＝f(t)，经长期观测，y＝f(t)的曲线可近似地看成是函数y＝Acosωt＋b，下表是某日各时的浪高数据：‎ t/时 ‎0‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎15‎ ‎18‎ ‎21‎ ‎24‎ y/米 ‎2‎ ‎1‎ ‎2‎ ‎0.99‎ ‎2‎ 则最能近似地表示表中数据间对应关系的函数是(　　)‎ A．y＝cost＋1 B．y＝cost＋ C．y＝2cost＋ D．y＝cos6πt＋ ‎[答案]　B ‎[解析]　∵T＝12－0＝12，∴ω＝＝＝.‎ 又最大值为2，最小值为1，‎ 则解得A＝，b＝，‎ ‎∴y＝cost＋.‎ 第Ⅱ卷(非选择题　共90分)‎ 二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．若cos(75°＋α)＝，其中α为第三象限角，则cos(105°－α)＋sin(α－105°)＝________.‎ ‎[答案]　 ‎[解析]　cos(105°－α)＋sin(α－105°)＝－cos(75°＋α)－sin(α＋75°)．∵180°<α<270°，∴255°<α＋75°<345°.又∵cos(α＋75°)＝，∴sin(α＋75°)＝－.∴原式＝－＋＝.‎ ‎14．函数y＝lg(sinx)＋的定义域为________________．‎ ‎[答案]　[－4，－π)∪(0，π)‎ ‎[解析]　由已知，得解得 即x∈[－4，－π)∪(0，π)．‎ ‎15．据市场调查，某种商品每件的售价按月呈f(x)＝Asin(ωx＋φ)＋B(A>0，ω>0，|φ|<)的模型波动(x为月份)，已知3月份达到最高价8千元，7月份价格最低为4千元，则f(x)＝________.‎ ‎[答案]　2sin＋6‎ ‎[解析]　由题意得解得A＝2，B＝6.‎ 周期T＝2(7－3)＝8，∴ω＝＝.‎ ‎∴f(x)＝2sin＋6.‎ 又当x＝3时，y＝8，‎ ‎∴8＝2sin＋6.‎ ‎∴sin＝1，取φ＝－.‎ ‎∴f(x)＝2sin＋6.‎ ‎16．关于函数f(x)＝4sin(2x＋)(x∈R)，有下列命题：‎ ‎①函数y＝f(x)的表达式可改写为y＝4cos(2x－)；‎ ‎②函数y＝f(x)是以2π为最小正周期的周期函数；‎ ‎③函数y＝f(x)的图象关于点(－，0)对称；‎ ‎④函数y＝f(x)的图象关于直线x＝－对称．‎ 其中，正确的是________．(填上你认为正确命题的序号)‎ ‎[答案]　①③‎ ‎[解析]　①f(x)＝4sin(2x＋)＝4cos(－2x－)＝4cos(－2x＋)＝4cos(2x－)．②T＝＝π，最小正周期为π.③∵2x＋＝kπ，当k＝0时，x＝－，函数f(x)关于点(－，0)对称．④2x＋＝＋kπ，当x＝－时，k＝－，与k∈Z矛盾．∴①③正确．‎ 三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．(本题满分10分)(1)已知角α的终边经过点P(4，－3)，求2sinα＋cosα的值；‎ ‎(2)已知角α的终边经过点P(‎4a，－‎3a)(a≠0)，求2sinα＋cosα的值；‎ ‎(3)已知角α终边上一点P与x轴的距离与y轴的距离之比为34，求2sinα＋cosα的值．‎ ‎[解析]　(1)∵r＝＝5，∴sinα＝＝－，cosα＝＝，∴2sinα＋cosα＝－＋＝－.‎ ‎(2)∵r＝＝5|a|，∴当a>0时，r＝‎5a，∴sinα＝＝－，cosα＝，∴2sinα＋cosα＝－；当a<0时，r＝－‎5a，∴sinα＝＝，cosα＝－，‎ ‎∴2sinα＋cosα＝.‎ ‎(3)当点P在第一象限时，sinα＝，cosα＝，‎ ‎2sinα＋cosα＝2；当点P在第二象限时，sinα＝，‎ cosα＝－，2sinα＋cosα＝；当点P在第三象限时，sinα＝－，cosα＝－，2sinα＋cosα＝－2；‎ 当点P在第四象限时，sinα＝－，cosα＝，2sinα＋cosα＝－.‎ ‎18．(本题满分12分)已知tanα、是关于x的方程x2－kx＋k2－3＝0的两实根，且3π<α<π，求cos(3π＋α)－sin(π＋α)的值．‎ ‎[解析]　由题意，根据韦达定理，得tanα＝k2－3＝1，∴k ‎＝±2.又∵3π<α<π，∴tanα>0，>0，‎ ‎∴tanα＋＝k>0，即k＝2，而k＝－2舍去，∴tanα＝＝1，∴sinα＝cosα＝－，∴cos(3π＋α)－sin(π＋α)＝sinα－cosα＝0.‎ ‎19．(本题满分12分)已知x∈[－，]，‎ ‎(1)求函数y＝cosx的值域；‎ ‎(2)求函数y＝－3sin2x－4cosx＋4的值域．‎ ‎[解析]　(1)∵y＝cosx在[－，0]上为增函数，在[0，]上为减函数，‎ ‎∴当x＝0时，y取最大值1；‎ x＝时，y取最小值－.‎ ‎∴y＝cosx的值域为[－，1]．‎ ‎(2)原函数化为：y＝3cos2x－4cosx＋1，‎ 即y＝3(cosx－)2－，‎ 由(1)知，cosx∈[－，1]，故y的值域为[－，]．‎ ‎20．(本题满分12分)已知函数f(x)＝3sin－1，x∈R.‎ 求：(1)函数f(x)的最小值及此时自变量x的取值集合；‎ ‎(2)函数y＝sinx的图象经过怎样的变换得到函数f(x)＝3sin－1的图象？‎ ‎[解析]　(1)函数f(x)的最小值是3×(－1)－1＝－4，此时有x＋＝2kπ－，解得x＝4kπ－(k∈Z)，‎ 即函数f(x)的最小值是－4，此时自变量x的取值集合是.‎ ‎(2)步骤是：‎ ‎①将函数y＝sinx的图象向左平移个单位长度，得到函数y＝sin的图象；‎ ‎②将函数y＝sin的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变)，得到函数y＝sin的图象；‎ ‎③将函数y＝sin的图象上所有点的纵坐标伸长为原来的3倍(横坐标不变)，得到函数y＝3sin的图象；‎ ‎④将函数y＝3sin的图象向下平移1个单位长度，得函数y＝3sin－1的图象．‎ ‎21．(本题满分12分)如图，某市拟在长为‎8 km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y＝Asinωx(A>0，ω>0)，x∈[0,4]的图象，且图象的最高点为S(3,2)；赛道的后一部分为折线段MNP.试求A、ω的值和M、P两点间的距离．‎ ‎[解析]　∵函数y＝Asinωx(A>0，ω>0)图象的最高点为S(3,2)，‎ ‎∴A＝2.由图象，得＝3，∴T＝12.‎ 又T＝，∴ω＝，即y＝2sinx.‎ 当x＝4时，y＝2sin＝3.‎ ‎∴M(4,3)．又P(8,0)．‎ ‎∴|MP|＝＝5，‎ 即MP的长是5.‎ ‎22．(本题满分12分)已知函数f(x)＝Asin(ωx＋φ)＋B(A>0，ω>0)的一系列对应值如下表：‎ x ‎－ y ‎－1‎ ‎1‎ ‎3‎ ‎1‎ ‎－1‎ ‎1‎ ‎3‎ ‎(1)根据表格提供的数据求函数f(x)的一个解析式；‎ ‎(2)根据(1)的结果，若函数y＝f(kx)(k>0)的周期为，当x∈[0，]时，方程f(kx)＝m恰有两个不同的解，求实数m的取值范围．‎ ‎[解析]　(1)设f(x)的最小正周期为T，则T＝－(－)＝2π，‎ 由T＝，得ω＝1，又，‎ 解得，令ω·＋φ＝，‎ 即＋φ＝，‎ 解得φ＝－，‎ ‎∴f(x)＝2sin(x－)＋1.‎ ‎(2)∵函数y＝f(kx)＝2sin(kx－)＋1的周期为，又k>0，∴k＝3，令t＝3x－，‎ ‎∵x∈[0，]，∴t∈[－，]，‎ 如图，sint＝s在[－，]上有两个不同的解，则s∈[，1]，‎ ‎∴方程 f(kx)＝m在x∈[0，]时恰好有两个不同的解，则m∈[＋1,3]，即实数m的取值范围是[＋1,3]．‎