【数学】2019届一轮复习人教A版(文)第一章第1讲集合学案
第一章 集合与常用逻辑用语
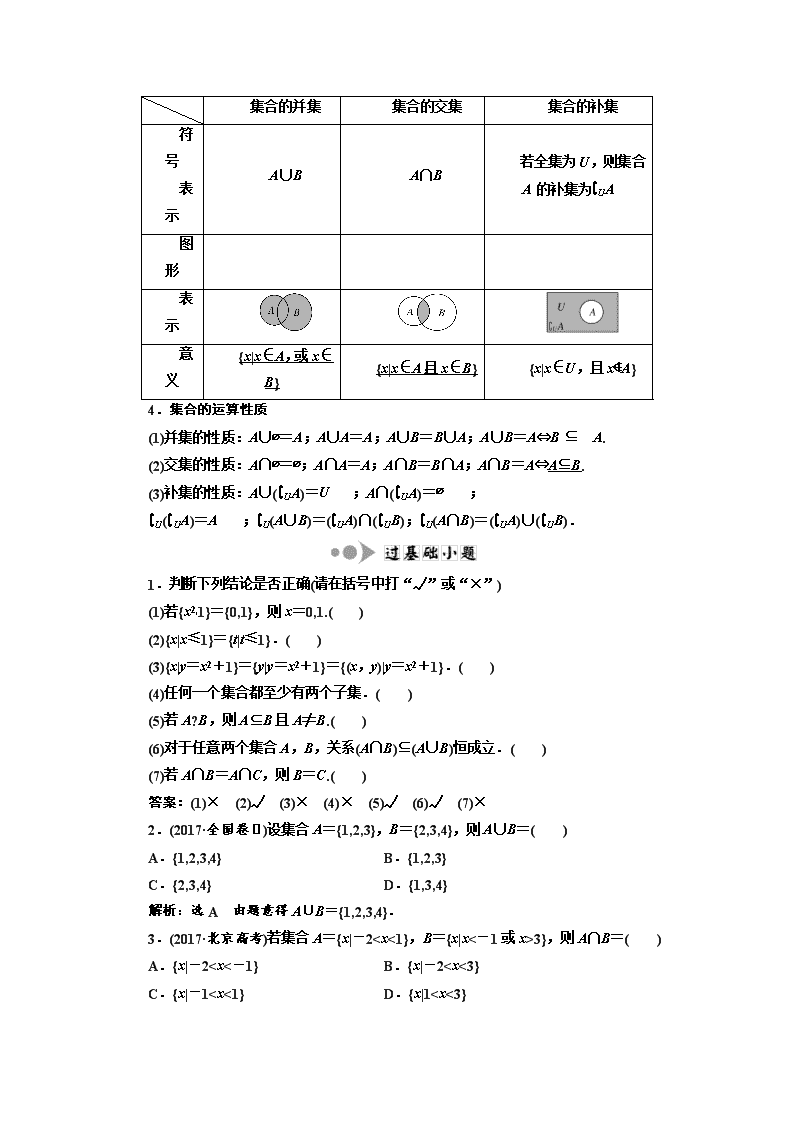
第一节集__合
1.集合的相关概念
(1)集合元素的三个特性:确定性、无序性、互异性.
(2)元素与集合的两种关系:属于,记为;不属于,记为.
(3)集合的三种表示方法:列举法、描述法、图示法.
(4)五个特定的集合:
集合
自然数集
正整数集
整数集
有理数集
实数集
符号
或N+
2.集合间的基本关系
表示
关系
文字语言
符号语言
记法
基本关系
子集
集合A的元素都是集合B的元素
x∈A⇒
x∈B
A⊆B或B⊇A
真子集
集合A是集合B的子集,且集合B中至少有一个元素不属于A
A⊆B,且
∃x0∈B,
x0∉A
A?B或
B?A
相等
集合A,B的元素完全相同
A⊆B,
B⊆A
A=B
空集
不含任何元素的集合.空集是任何集合A的子集,是任何非空集合B的真子集
∀x,x∉∅,∅⊆A,∅?B(B≠∅)
∅
3.集合的基本运算
集合的并集
集合的交集
集合的补集
符号
表示
A∪B
A∩B
若全集为U,则集合A的补集为∁UA
图形
表示
意义
{x|x∈A,或x∈B}
{x|x∈A,且x∈B}
{x|x∈U,且x∉A}
4.集合的运算性质
(1)并集的性质:A∪∅=A;A∪A=A;A∪B=B∪A;A∪B=A⇔BA.
(2)交集的性质:A∩∅=∅;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆B.
(3)补集的性质:A∪(∁UA)=;A∩(∁UA)=;
∁U(∁UA)=;∁U(A∪B)=(∁UA)∩(∁UB);∁U(A∩B)=(∁UA)∪(∁UB).
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)若{x2,1}={0,1},则x=0,1.( )
(2){x|x≤1}={t|t≤1}.( )
(3){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( )
(4)任何一个集合都至少有两个子集.( )
(5)若A?B,则A⊆B且A≠B.( )
(6)对于任意两个集合A,B,关系(A∩B)⊆(A∪B)恒成立.( )
(7)若A∩B=A∩C,则B=C.( )
答案:(1)× (2)√ (3)× (4)× (5)√ (6)√ (7)×
2.(2017·全国卷Ⅱ)设集合A={1,2,3},B={2,3,4},则A∪B=( )
A.{1,2,3,4} B.{1,2,3}
C.{2,3,4} D.{1,3,4}
解析:选A 由题意得A∪B={1,2,3,4}.
3.(2017·北京高考)若集合A={x|-2
3},则A∩B=( )
A.{x|-20},则集合A与B的关系是( )
A.B⊆A B.B⊇A
C.B∈A D.A∈B
解析:选A 因为A={x|-x2-x+2<0}={x|x>1或x<-2},B={x|2x-5>0}=.
在数轴上标出集合A与集合B,如图所示,
可知,B⊆A.
[题型技法]
判断集合间关系的3种方法
列举法
根据题中限定条件把集合元素表示出来,然后比较集合元素的异同,从而找出集合之间的关系.(如第1题)
结构法
从元素的结构特点入手,结合通分、化简、变形等技巧,从元素结构上找差异进行判断.(如第2题)
数轴法
在同一个数轴上表示出两个集合,比较端点之间的大小关系,从而确定集合与集合之间的关系.(如第3题)
(二)迁移考——利用集合间关系求参数
4.(2018·云南师大附中模拟)集合A={x|x2-a≤0},B={x|x<2},若A⊆B,则实数a的取值范围是( )
A.(-∞,4] B.(-∞,4)
C.[0,4] D.(0,4)
解析:选B 集合A就是不等式x2-a≤0,即x2≤a的解集.①当a<0时,不等式无解,故A=∅.此时显然满足A⊆B.②当a=0时,不等式为x2≤0,解得x=0,所以A={0}.显然{0}⊆{x|x<2},即满足A⊆B.③当a>0时,解不等式x2≤a,得-≤x≤.所以A=[-, ].由A⊆B可得,<2,解得00,解得x>2,故B=(2,+∞).把两个集合A,B在数轴上表示出来,如图,可知A∩B=(2,5].
2.(2018·湖南湘潭模拟)已知全集U=R,集合M={x||x|<1},N={y|y=2x,x∈R},则集合∁U(M∪N)=( )
A.(-∞,-1] B.(-1,2)
C.(-∞,-1]∪[2,+∞) D.[2,+∞)
解析:选A 解|x|<1,得-10},B={x|-2≤x≤2},则如图所示阴影部分所表示的集合为( )
A.{x|-2≤x<4} B.{x|x≤2或x≥4}
C.{x|-2≤x≤-1} D.{x|-1≤x≤2}
解析:选D 依题意得A={x|x<-1或x>4},因此∁RA={x|-1≤x≤4},题中的阴影部分所表示的集合为(∁RA)∩B={x|-1≤x≤2},选D.
[解题师说]
1.掌握“4种技巧”
(1)先“简”后“算”:进行集合的基本运算之前要先对其进行化简,化简时要准确把握元素的性质特征,区分数集与点集等.如求集合P=的补集,要先进行化简,若直接否定集合P中元素的性质特征,就会误以为∁RP=,导致漏解.
(2)遵“规”守“矩”:定义是进行集合基本运算的依据,交集的运算要抓住“公共元素”,补集的运算要关注“你有我无”的元素.
(3)活“性”减“量”:灵活利用交集与并集以及补集的运算性质,特别是摩根定律,即∁U(M∩N)=(∁UM)∪(∁UN),∁U(M∪N)=(∁UM)∩(∁UN)等简化运算,减少运算量.
(4)借“形”助“数”:在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化,用数轴表示时要注意端点值的取舍.(如典题领悟第1题)
2.谨防“2种失误”
(1)进行集合基本运算时要注意对应不等式端点值的处理,尤其是求解集合补集的运算,一定要注意端点值的取舍.(如典题领悟第2题)
(2)求集合的补集时,既要注意全集是什么,又要注意求补集的步骤,一般先求出原来的集合,然后求其补集,否则容易漏解.(如典题领悟第3题、冲关演练第3题)
[冲关演练]
1.(2017·天津高考)设集合A={1,2,6},B={2,4},C={x∈R|-1≤x≤5},则(A∪B)∩C=( )
A.{2} B.{1,2,4}
C.{1,2,4,6} D.{x∈R|-1≤x≤5}
解析:选B A∪B={1,2,4,6},又C={x∈R|-1≤x≤5},则(A∪B)∩C={1,2,4}.
2.(2018·合肥质量检测)已知集合A=[1,+∞),B=,若A∩B≠∅,则实数a的取值范围是( )
A.[1,+∞) B.
C. D.(1,+∞)
解析:选A 因为A∩B≠∅,所以解得a≥1.
3.(2018·皖北协作区联考)已知集合A={y|y=},B={x|y=lg(x-2x2)},则∁R(A∩B)=( )
A. B.(-∞,0)∪
C. D.(-∞,0]∪
解析:选D 因为A={y|y=}=[0,+∞),B={x|y=lg(x-2x2)}=,所以A∩B=,所以∁R(A∩B)=(-∞,0]∪.
以集合为载体的新定义问题,是高考命制创新型试题的一个热点,常见的命题形式有新概念、新性质、新法则等,一般以选择题或填空题形式出现,难度中等或偏上.
[典题领悟]
1.设集合A={-1,0,1},集合B={-1,1,2,3},定义A#B=,则A#B中元素的个数是( )
A.5 B.7
C.10 D.15
解析:选B 因为x∈A,所以x可取-1,0,1;
因为y∈B,所以y可取-1,1,2,3.
则z=的结果如下表所示:
y
x
-1
1
2
3
-1
1
-1
-
-
0
0
0
0
0
1
-1
1
故A#B中元素有-1,-,-,0,,,1,共7个,故选B.
2.已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,都存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M=;
②M={(x,y)|y=log2x};
③M={(x,y)|y=ex-2};
④M={(x,y)|y=sin x+1}.
其中是“垂直对点集”的序号是( )
A.①④ B.②③
C.③④ D.②④
解析:选C 记A(x1,y1),B(x2,y2),则由x1x2+y1y2=0得OA⊥OB.对于①,对任意A∈M,不存在B∈M,使得OA⊥OB.对于②,当A为点(1,0)时,不存在B∈M满足题意.对于③④,对任意A∈M,过原点O可作直线OB⊥OA,它们都与函数y=ex-2及y=sin x+1的图象相交,即③④满足题意,故选C.
3.设集合A={-1,0,1},集合B={0,1,2,3},定义A*B={(x,y)|x∈A∩B,y∈A∪B},则A*B中元素的个数是( )
A.7 B.10
C.25 D.52
解析:选B 因为A={-1,0,1},B={0,1,2,3},
所以A∩B={0,1},A∪B={-1,0,1,2,3}.
由x∈A∩B,可知x可取0,1;
由y∈A∪B,可知y可取-1,0,1,2,3.
所以元素(x,y)的所有结果如下表所示:
y
x
-1
0
1
2
3
0
(0,-1)
(0,0)
(0,1)
(0,2)
(0,3)
1
(1,-1)
(1,0)
(1,1)
(1,2)
(1,3)
所以A*B中的元素共有10个.
[解题师说]
与集合相关的新定义问题的解题思路
(1)紧扣“新”定义:分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题的关键所在.
(2)把握“新”性质:集合的性质(概念、元素的性质、运算性质等)是破解新定义型集合问题的基础,也是突破口,在解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之处用好集合的性质.
(3)遵守“新”法则:准确把握新定义的运算法则,将其转化为集合的交集、并集与补集的运算即可.
[冲关演练]
1.定义集合的商集运算为=,已知集合A={2,4,6},B=
,则集合∪B中的元素个数为( )
A.6 B.7
C.8 D.9
解析:选B 由题意知,B={0,1,2},=0,,,,1,,则∪B=,共有7个元素,故选B.
2.(2018·武昌调研)设A,B是两个非空集合,定义集合A-B={x|x∈A,且x∉B},若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=( )
A.{0,1} B.{1,2}
C.{0,1,2} D.{0,1,2,5}
解析:选D 因为A={x∈N|0≤x≤5},所以A={0,1,2,3,4,5}.解不等式x2-7x+10<0,即(x-2)(x-5)<0,得20时,∵A={x|-10},Q={x|x2+ax+b≤0}.若P∪Q=R,且P∩Q=(2,3],则a+b=( )
A.-5 B.5
C.-1 D.1
解析:选A P={y|y2-y-2>0}={y|y>2或y<-1}.由P∪Q=R及P∩Q=(2,3],得Q=[-1,3],所以-a=-1+3,b=-1×3,即a=-2,b=-3,a+b=-5,故选A.
6.设集合A={x|(x-a)2<1},且2∈A,3∉A,则实数a的取值范围是________.
解析:由题意得
即所以1<a≤2.
答案:(1,2]
7.设集合A={x|x2-x-2≤0},B={x|x<1,且x∈Z},则A∩B=________.
解析:依题意得A={x|(x+1)(x-2)≤0}={x|-1≤x≤2},因此A∩B={x|-1≤x<1,x∈Z}={-1,0}.
答案:{-1,0}
8.设全集为R,集合A={x|x2-9<0},B={x|-1<x≤5},则A∩(∁RB)=______________.
解析:由题意知,A={x|x2-9<0}={x|-3<x<3},
∵B={x|-1<x≤5},∴∁RB={x|x≤-1或x>5}.
∴A∩(∁RB)={x|-3<x<3}∩{x|x≤-1或x>5}={x|-3<x≤-1}.
答案:{x|-3<x≤-1}
9.(2018·江西玉山一中月考)已知集合A={x|3≤3x≤27},B={x|log2x>1}.
(1)分别求A∩B,(∁RB)∪A;
(2)已知集合C={x|11,即log2x>log22,
∴x>2,∴B={x|x>2}.∴A∩B={x|2m+2},
因为A⊆∁RB,
所以m-2>3或m+2<-1,
即m>5或m<-3.
因此实数m的取值范围是(-∞,-3)∪(5,+∞).
6.若集合M={x|-3≤x≤4},集合P={x|2m-1≤x≤m+1}.
(1)证明M与P不可能相等;
(2)若集合M与P中有一个集合是另一个集合的真子集,求实数m的取值范围.
解:(1)证明:若M=P,则-3=2m-1且4=m+1,
解得m=-1且m=3,不成立.
故M与P不可能相等.
(2)若P?M,当P≠∅时,有
或解得-1≤m≤2;
当P=∅时,有2m-1>m+1,解得m>2,即m≥-1;
若M?P,则或无解.
综上可知,当有一个集合是另一个集合的真子集时,只能是P?M,此时必有m≥-1,
即实数m的取值范围为[-1,+∞).