- 2021-02-27 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河南省六市(南阳市、驻马店市、信阳市等)2020届高三第一次模拟调研数学(理)试题 Word版含解析
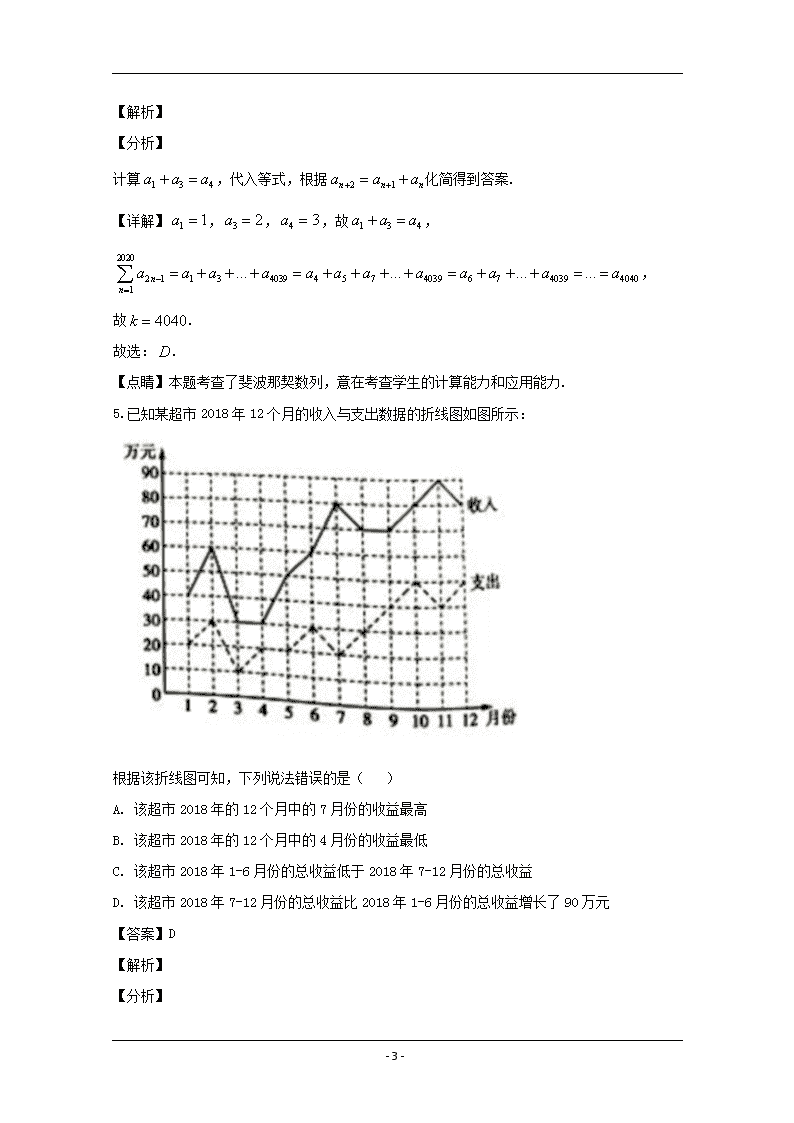
www.ks5u.com 2020年河南省六市高三第一次模拟调研试题理科数学 第Ⅰ卷选择题(共60分) 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若复数满足,则( ) A. B. C. D. 【答案】C 【解析】 【分析】 化简得到,,再计算复数模得到答案. 【详解】,故, 故,. 故选:. 【点睛】本题考查了复数的化简,共轭复数,复数模,意在考查学生的计算能力. 2.集合真子集的个数为( ) A. 7 B. 8 C. 31 D. 32 【答案】A 【解析】 【分析】 计算,再计算真子集个数得到答案. 【详解】,故真子集个数为:. 故选:. 【点睛】本题考查了集合的真子集个数,意在考查学生的计算能力. - 22 - 3.五行学说是华夏民族创造的哲学思想,是华夏文明重要组成部分.古人认为,天下万物皆由金、木、水、火、土五类元素组成,如图,分别是金、木、水、火、土彼此之间存在的相生相克的关系.若从5类元素中任选2类元素,则2类元素相生的概率为( ) A. B. C. D. 【答案】A 【解析】 【分析】 列举出金、木、水、火、土任取两个的所有结果共10种,其中2类元素相生的结果有5种,再根据古典概型概率公式可得结果. 【详解】金、木、水、火、土任取两类,共有: 金木、金水、金火、金土、木水、木火、木土、水火、水土、火土10种结果, 其中两类元素相生的有火木、火土、木水、水金、金土共5结果, 所以2类元素相生的概率为,故选A. 【点睛】本题主要考查古典概型概率公式的应用,属于基础题,利用古典概型概率公式求概率时,找准基本事件个数是解题的关键,基本亊件的探求方法有 (1)枚举法:适合给定的基本事件个数较少且易一一列举出的;(2)树状图法:适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时,一定要按顺序逐个写出:先,…. ,再,…..依次….… 这样才能避免多写、漏写现象的发生. 4.著名的斐波那契数列:1,1,2,3,5,8,…,满足,,,若,则( ) A. 2020 B. 4038 C. 4039 D. 4040 【答案】D - 22 - 【解析】 【分析】 计算,代入等式,根据化简得到答案. 【详解】,,,故, , 故. 故选:. 【点睛】本题考查了斐波那契数列,意在考查学生的计算能力和应用能力. 5.已知某超市2018年12个月的收入与支出数据的折线图如图所示: 根据该折线图可知,下列说法错误的是( ) A. 该超市2018年的12个月中的7月份的收益最高 B. 该超市2018年的12个月中的4月份的收益最低 C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益 D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元 【答案】D 【解析】 【分析】 - 22 - 用收入减去支出,求得每月收益,然后对选项逐一分析,由此判断出说法错误的选项. 【详解】用收入减去支出,求得每月收益(万元),如下表所示: 月份 1 2 3 4 5 6 7 8 9 10 11 12 收益 20 30 20 10 30 30 60 40 30 30 50 30 所以月收益最高,A选项说法正确;月收益最低,B选项说法正确;月总收益万元,月总收益万元,所以前个月收益低于后六个月收益,C选项说法正确,后个月收益比前个月收益增长万元,所以D选项说法错误.故选D. 【点睛】本小题主要考查图表分析,考查收益的计算方法,属于基础题. 6.设函数,则函数的图像可能为( ) A. B. C. D. 【答案】B 【解析】 【分析】 根据函数为偶函数排除,再计算排除得到答案. 【详解】定义域为: ,函数为偶函数,排除 ,排除 故选 - 22 - 【点睛】本题考查了函数图像,通过函数的单调性,奇偶性,特殊值排除选项是常用的技巧. 7.设,满足约束条件,若最大值为,则的展开式中项的系数为( ) A. 60 B. 80 C. 90 D. 120 【答案】B 【解析】 【分析】 画出可行域和目标函数,根据平移得到,再利用二项式定理计算得到答案. 【详解】如图所示:画出可行域和目标函数, ,即,故表示直线与截距的倍, 根据图像知:当时,的最大值为,故. 展开式的通项为:, 取得到项的系数为:. 故选:. 【点睛】本题考查了线性规划求最值,二项式定理,意在考查学生 - 22 - 计算能力和综合应用能力. 8.已知圆锥的高为3,底面半径为,若该圆锥的顶点与底面的圆周都在同一个球面上,则这个球的体积与圆锥的体积的比值为( ) A. B. C. D. 【答案】B 【解析】 【分析】 计算求半径为,再计算球体积和圆锥体积,计算得到答案. 【详解】如图所示:设球半径为,则,解得. 故求体积为:,圆锥的体积:,故. 故选:. 【点睛】本题考查了圆锥,球体积,圆锥的外接球问题,意在考查学生的计算能力和空间想象能力. 9.已知抛物线:的焦点为,准线为,是上一点,直线与抛物线交于,两点,若,则为( ) A. B. 40 C. 16 D. 【答案】D - 22 - 【解析】 【分析】 如图所示,过分别作于,于,利用和,联立方程组计算得到答案. 【详解】如图所示:过分别作于,于. ,则, 根据得到:,即, 根据得到:,即, 解得,,故. 故选:. 【点睛】本题考查了抛物线中弦长问题,意在考查学生的计算能力和转化能力. 10.已知为圆:上任意一点,,若线段的垂直平分线交直线于点,则点的轨迹方程为( ) A. B. - 22 - C. () D. () 【答案】B 【解析】 【分析】 如图所示:连接,根据垂直平分线知,,故轨迹为双曲线,计算得到答案. 【详解】如图所示:连接,根据垂直平分线知, 故,故轨迹为双曲线, ,,,故,故轨迹方程为. 故选:. 【点睛】本题考查了轨迹方程,确定轨迹方程为双曲线是解题的关键. 11.已知是等差数列的前项和,若,设,则数列的前项和取最大值时的值为( ) - 22 - A. 2020 B. 20l9 C. 2018 D. 2017 【答案】B 【解析】 【分析】 根据题意计算,,,计算,,,得到答案. 【详解】是等差数列的前项和,若, 故,,,,故, 当时,,,, , 当时,,故前项和最大. 故选:. 【点睛】本题考查了数列和的最值问题,意在考查学生对于数列公式方法的综合应用. 12.方程在区间内的所有解之和等于( ) A. 4 B. 6 C. 8 D. 10 【答案】C 【解析】 【分析】 画出函数和的图像,和均关于点中心对称,计算得到答案. 【详解】,验证知不成立,故, - 22 - 画出函数和的图像, 易知:和均关于点中心对称,图像共有8个交点, 故所有解之和等于. 故选:. 【点睛】本题考查了方程解的问题,意在考查学生的计算能力和应用能力,确定函数关于点中心对称是解题的关键. 第Ⅱ卷非选择题(共90分) 二、填空题:本大题共4小题,每小题5分,共20分. 13.已知向量,,若,则________. 【答案】10 【解析】 【分析】 根据垂直得到,代入计算得到答案. 【详解】,则,解得, 故,故. 故答案为:. 【点睛】本题考查了根据向量垂直求参数,向量模,意在考查学生的计算能力. - 22 - 14.设函数,则满足的的取值范围为________. 【答案】 【解析】 【分析】 当时,函数单调递增,当时,函数为常数,故需满足,且,解得答案. 【详解】,当时,函数单调递增,当时,函数为常数, 需满足,且,解得. 故答案为:. 【点睛】本题考查了根据函数单调性解不等式,意在考查学生对于函数性质的灵活运用. 15.六位同学坐在一排,现让六位同学重新坐,恰有两位同学坐自己原来的位置,则不同的坐法有________种(用数字回答). 【答案】135 【解析】 【分析】 根据题意先确定2个人位置不变,共有种选择,再确定4个人坐4个位置,但是不能坐原来的位置,计算得到答案. 【详解】根据题意先确定2个人位置不变,共有种选择. 再确定4个人坐4个位置,但是不能坐原来的位置,共有种选择, 故不同的坐法有. 故答案为:. 【点睛】本题考查了分步乘法原理,意在考查学生的计算能力和应用能力. 16.若方程有两个不等实根,则实数的取值范围是_____________. 【答案】 - 22 - 【解析】 【详解】由知x>0,故. 令,则. 当时,;当时,. 所以在(0,e)上递增,在(e,+)上递减. 故,即. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分. 17.如图中,为的中点,,,. (1)求边的长; (2)点在边上,若是的角平分线,求的面积. 【答案】(1)10;(2). 【解析】 【分析】 (1)由题意可得cos∠ADB=﹣cos∠ADC,由已知利用余弦定理可得:9+BD2﹣52+9+BD2﹣16=0,进而解得BC的值.(2)由(1)可知△ADC为直角三角形,可求S△ADC6,S△ABC=2S△ADC=12,利用角平分线的性质可得,根据S△ABC=S△BCE+S△ACE可求S△BCE的值. 【详解】(1)因在边上,所以, 在和中由余弦定理,得, - 22 - 因为,,,, 所以,所以,. 所以边的长为10. (2)由(1)知为直角三角形,所以,. 因为是的角平分线, 所以. 所以,所以. 即的面积为. 【点睛】本题主要考查了余弦定理,三角形的面积公式,角平分线的性质在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题. 18.在四棱椎中,四边形为菱形,,,,,,分别为,中点.. (1)求证:; (2)求平面与平面所成锐二面角的余弦值. 【答案】(1)证明见解析;(2). 【解析】 【分析】 (1)证明,得到平面,得到证明. (2)以点为坐标原点,建立如图所示的空间直角坐标系,平面的一个法向量为,平面的一个法向量为,计算夹角得到答案. - 22 - 【详解】(1)因为四边形是菱形,且,所以是等边三角形, 又因为是的中点,所以,又因为,,所以, 又,,,所以, 又,,所以平面,所以, 又因为是菱形,,所以,又, 所以平面,所以. (2)由题意结合菱形的性质易知,,, 以点为坐标原点,建立如图所示空间直角坐标系, 则,,,,, 设平面的一个法向量为,则:, 据此可得平面的一个法向量为, 设平面的一个法向量为,则:, 据此可得平面的一个法向量为, , 平面与平面所成锐二面角的余弦值. 【点睛】本题考查了线线垂直,二面角,意在考查学生的计算能力和空间想象能力. - 22 - 19.设椭圆的左右焦点分别为,离心率是,动点在椭圆上运动,当轴时,. (1)求椭圆的方程; (2)延长分别交椭圆于点(不重合).设,求的最小值. 【答案】(1);(2) 【解析】 【分析】 (1)根据题意直接计算得到,,得到椭圆方程. (2)不妨设,且,设,代入 数据化简得到 ,故,得到答案. 【详解】(1),所以,,化简得, 所以,,所以方程为; (2)由题意得,不在轴上,不妨设,且,设, 所以由,得, 所以, - 22 - 由,得,代入, 化简得:, 由于,所以,同理可得, 所以,所以当时,最小为 【点睛】本题考查了椭圆方程,椭圆中的向量运算和最值,意在考查学生的计算能力和综合应用能力. 20.已知函数()在定义域内有两个不同的极值点. (1)求实数的取值范围; (2)若有两个不同的极值点,,且,若不等式恒成立.求正实数的取值范围. 【答案】(1);(2). 【解析】 【分析】 (1)求导得到有两个不相等实根,令,计算函数单调区间得到值域,得到答案. (2),是方程的两根,故,化简得到,设函数,讨论范围,计算最值得到答案. 【详解】(1)由题可知有两个不相等的实根, 即:有两个不相等实根,令, ,, ,;,, - 22 - 故在上单增,在上单减,∴. 又,时,;时,, ∴,即. (2)由(1)知,,是方程的两根, ∴,则 因为在单减,∴,又,∴ 即,两边取对数,并整理得: 对恒成立, 设,, , 当时,对恒成立, ∴在上单增,故恒成立,符合题意; 当时,,时, ∴在上单减,,不符合题意. 综上,. 【点睛】本题考查了根据极值点求参数,恒成立问题,意在考查学生的计算能力和综合应用能力. 21.某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次 - 22 - 普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.方案①:将每个人的血分别化验,这时需要验1000次.方案②:按个人一组进行随机分组,把从每组个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这个人的血只需检验一次(这时认为每个人的血化验次);否则,若呈阳性,则需对这个人的血样再分别进行一次化验,这样,该组个人的血总共需要化验次.假设此次普查中每个人的血样化验呈阳性的概率为,且这些人之间的试验反应相互独立. (1)设方案②中,某组个人的每个人的血化验次数为,求的分布列; (2)设,试比较方案②中,分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数) 【答案】(1)分布列见解析;(2)406. 【解析】 【分析】 (1)计算个人的血混合后呈阴性反应的概率为,呈阳性反应的概率为,得到分布列. (2)计算,代入数据计算比较大小得到答案. 【详解】(1)设每个人的血呈阴性反应的概率为,则. 所以个人的血混合后呈阴性反应的概率为,呈阳性反应的概率为. 依题意可知,,所以的分布列为: (2)方案②中. 结合(1)知每个人的平均化验次数为: - 22 - 时,,此时1000人需要化验的总次数为690次, 时,,此时1000人需要化验的总次数为604次, 时,,此时1000人需要化验的次数总为594次, 即时化验次数最多,时次数居中,时化验次数最少,而采用方案①则需化验1000次, 故在这三种分组情况下,相比方案①, 当时化验次数最多可以平均减少次. 【点睛】本题考查了分布列,数学期望,意在考查学生的计算能力和应用能力. (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分. 选修4-4:坐标系与参数方程 22.心形线是由一个圆上的一个定点,当该圆在绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名,在极坐标系中,方程()表示的曲线就是一条心形线,如图,以极轴所在的直线为轴,极点为坐标原点的直角坐标系中.已知曲线的参数方程为(为参数). (1)求曲线的极坐标方程; (2)若曲线与相交于、、三点,求线段的长. 【答案】(1)();(2). 【解析】 【分析】 - 22 - (1)化简得到直线方程为,再利用极坐标公式计算得到答案. (2)联立方程计算得到,,计算得到答案 . 【详解】(1)由消得,即, 是过原点且倾斜角为的直线,∴的极坐标方程为(). (2)由得,∴, 由得∴,∴. 【点睛】本题考查了参数方程,极坐标方程,意在考查学生的计算能力和应用能力. 选修4-5:不等式选讲 23.已知函数. (1)当时,求不等式的解集; (2)若的解集包含,求的取值范围. 【答案】(1);(2). 【解析】 【分析】 (1)对范围分类整理得:,分类解不等式即可. (2)利用已知转化为“当时,”恒成立,利用绝对值不等式的性质可得:,问题得解. - 22 - 【详解】当时,, 当时,由得,解得; 当时,无解; 当时,由得,解得, 所以的解集为 (2)的解集包含等价于在上恒成立, 当时,等价于恒成立, 而,∴, 故满足条件的的取值范围是 【点睛】本题主要考查了含绝对值不等式的解法,还考查了转化能力及绝对值不等式的性质,考查计算能力,属于中档题. - 22 - - 22 -查看更多