- 2021-02-27 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册第12章全等三角形12
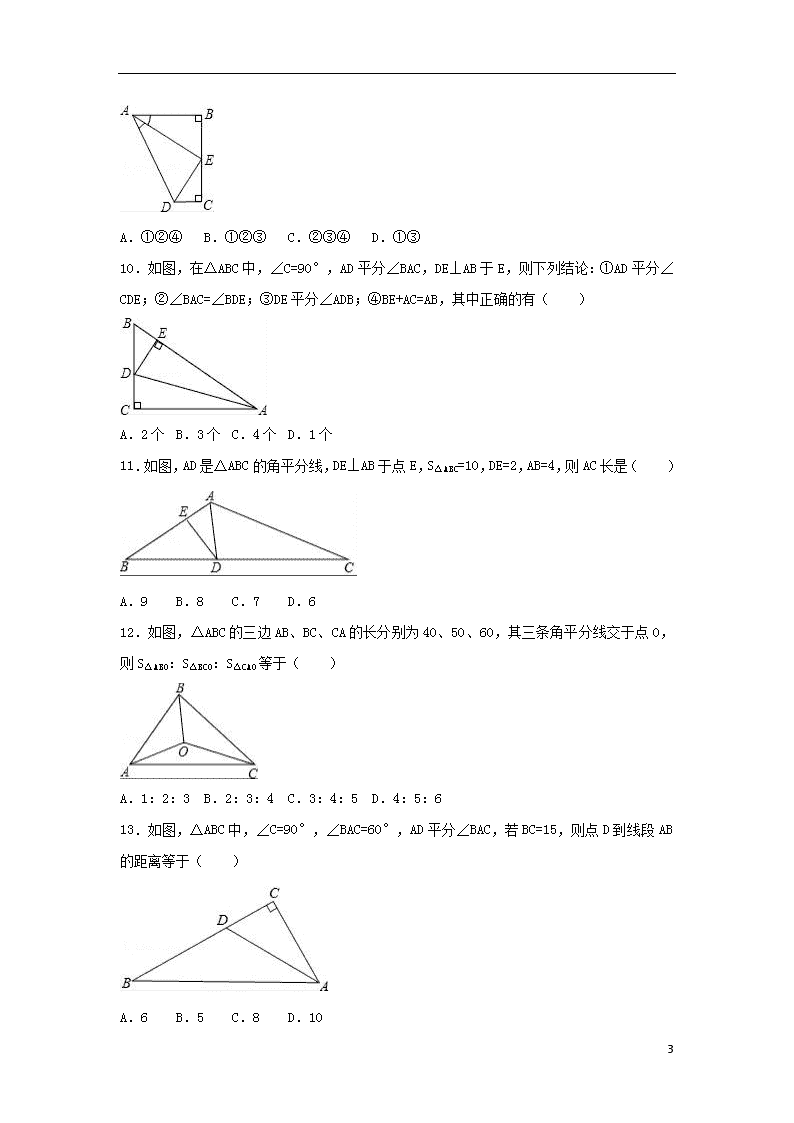
12.3 角的平分线的性质 学校:___________姓名:___________班级:___________ 一.选择题(共15小题) 1.如图,△ABC中,DE⊥AB,DF⊥AC,AD平分∠BAC,则下列结论中正确有( )个. (1)DE=DF;(2)AD⊥BC;(3)AE=AF;(4)∠EDA=∠FDA;(5)AB=AC;(6)∠B=∠C;(7)BD=CD. A.3 B.4 C.6 D.7 2.如图,∠1=∠2,PD⊥AB,PE⊥BC,垂足分别为D、E,则下列结论中错误的是( ) A.PD=PE B.BD=BE C.∠BPD=∠BPE D.BP=BE 3.点D到△ABC的两边AB、AC的距离相等,则点D在( ) A.BC的中线上 B.BC边的垂直平分线上 C.BC边的高线上 D.∠A的平分线所在的直线上 4.如图,有三条公路l1、l2、l3两两相交,要选择一地点建一座加油站,使加油站到三条公路的距离相等,不考虑其他因素,则符合条件的地点有( )个 A.1 B.2 C.3 D.4 5.观察图中尺规作图痕迹,下列说法错误的是( ) 17 A.OE是∠AOB的平分线 B.OC=OD C.点C、D到OE的距离不相等 D.∠AOE=∠BOE 6.如图,OP平分∠AOB,PC⊥OA于C,点D是OB上的动点,若PC=6cm则PD的长可以是( ) A.3cm B.4cm C.5cm D.7 cm 7.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论: ①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE; 其中正确的是( )个. A.1 B.2 C.3 D.4 8.下列画图的语句中,正确的为( ) A.画直线AB=10cm B.画射线OB=10cm C.延长射线BA到C,使BA=BC D.过直线AB外一点画一条直线和直线AB相交 9.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论: ①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD, 四个结论中成立的是( ) 17 A.①②④ B.①②③ C.②③④ D.①③ 10.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有( ) A.2个 B.3个 C.4个 D.1个 11.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=4,则AC长是( ) A.9 B.8 C.7 D.6 12.如图,△ABC的三边AB、BC、CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于( ) A.1:2:3 B.2:3:4 C.3:4:5 D.4:5:6 13.如图,△ABC中,∠C=90°,∠BAC=60°,AD平分∠BAC,若BC=15,则点D到线段AB的距离等于( ) A.6 B.5 C.8 D.10 17 14.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( ) A.3 B.4 C.5 D.6 15.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线. 如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A.角的内部到角的两边的距离相等的点在角的平分线上 B.角平分线上的点到这个角两边的距离相等 C.三角形三条角平分线的交点到三条边的距离相等 D.以上均不正确 二.填空题(共5小题) 16.把命题“角平分线上的点到这个角两边的距离相等”改写成“如果…,那么…、”的形式:如果 ,那么 . 17.如图,PM⊥OA,PN⊥OB,PM=PN,∠BOC=20°,则∠AOB= . 17 18.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是 . 19.如图l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有 处. 20.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是 . 三.解答题(共5小题) 21.阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据. 已知:如图,AM,BN,CP是△ABC的三条角平分线. 求证:AM、BN、CP交于一点. 证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F. ∵O是∠BAC角平分线AM上的一点( ), ∴OE=OF( ). 同理,OD=OF. ∴OD=OE( ). ∵CP是∠ACB的平分线( ), 17 ∴O在CP上( ). 因此,AM,BN,CP交于一点. 22.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长. 23.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N. 求证:∠OAB=∠OBA. 24.已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC. 17 求证:AB=AC. 25.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD于点F. 求证:DE=BF. 17 参考答案与试题解析 一.选择题(共15小题) 1. 解:∵在△ADE和△ADF中AD为公共边, 又∵DE⊥AB,DF⊥AC,AD平分∠BAC, ∴△AED≌△ADF, ∴DE=DF,AE=AF,∠EDA=∠FDA, 故(1)(3)(4)正确. 要想证得(2)(5)(6)(7)那就要求△ABC为等腰三角形,但是已知条件没有,从已知条件中也不能证得. ∴只有三个答案是正确的. 故选:A. 2. 解:由题意可得,∵∠1=∠2,PD⊥AB,PE⊥BC,∴∠BPD=∠BPD, 又BP为公共边,∴Rt△BPE≌Rt△BPD, ∴PD=PE,BD=BE, 所以D错, 故选:D. 3. 解:∵由角平分线上点到角两边距离相等的性质, ∴点D应在∠A的平分线上. 故选:D. 4. 解:如图所示: 符合条件的地点有4个, 故选:D. 17 5. 解:根据尺规作图的画法可知:OE是∠AOB的角平分线. A、OE是∠AOB的平分线,A正确; B、OC=OD,B正确; C、点C、D到OE的距离相等,C不正确; D、∠AOE=∠BOE,D正确. 故选:C. 6. 解:作PD⊥OA于D, ∵OP平分∠AOB,PC⊥OA,PD⊥OA, ∴PD=PC=6cm, 则PD的最小值是6cm, 故选:D. 7. 解:∵∠C=90°,AD平分∠BAC,DE⊥AB, ∴CD=DE,故①正确; 在Rt△ACD和Rt△AED中, , ∴Rt△ACD≌Rt△AED(HL), ∴AC=AE,∠ADC=∠ADE, ∴AC+BE=AE+BE=AB,故②正确; AD平分∠CDE,故④正确; 17 ∵∠B+∠BAC=90°, ∠B+∠BDE=90°, ∴∠BDE=∠BAC,故③正确; 综上所述,结论正确的是①②③④共4个. 故选:D. 8. 解:A、错误.直线没有长度; B、错误.射线没有长度; C、错误.射线有无限延伸性,不需要延长; D、正确. 故选:D. 9. 解:过E作EF⊥AD于F,如图, ∵AB⊥BC,AE平分∠BAD, ∴Rt△AEF≌Rt△AEB ∴BE=EF,AB=AF,∠AEF=∠AEB; 而点E是BC的中点, ∴EC=EF=BE,所以③错误; ∴Rt△EFD≌Rt△ECD, ∴DC=DF,∠FDE=∠CDE,所以②正确; ∴AD=AF+FD=AB+DC,所以④正确; ∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确. 故选:A. 17 10. 解:∵AD平分∠BAC ∴∠DAC=∠DAE ∵∠C=90°,DE⊥AB ∴∠C=∠E=90° ∵AD=AD ∴△DAC≌△DAE ∴∠CDA=∠EDA ∴①AD平分∠CDE正确; 无法证明∠BDE=60°, ∴③DE平分∠ADB错误; ∵BE+AE=AB,AE=AC ∴BE+AC=AB ∴④BE+AC=AB正确; ∵∠BDE=90°﹣∠B,∠BAC=90°﹣∠B ∴∠BDE=∠BAC ∴②∠BAC=∠BDE正确. 故选:B. 11. 解:过D作DF⊥AC于F, ∵AD是△ABC的角平分线,DE⊥AB, ∴DE=DF=2, ∵S△ADB=AB×DE=×4×2=4, ∵△ABC的面积为10, ∴△ADC的面积为10﹣4=6, ∴AC×DF=6, 17 ∴AC×2=6, ∴AC=6 故选:D. 12. 解:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F, ∵三条角平分线交于点O,OD⊥AB,OE⊥AC,OF⊥BC, ∴OD=OE=OF, ∴S△ABO:S△BCO:S△CAO=AB:BC:CA=4:5:6, 故选:D. 13. 解:作DE⊥AB于E, ∵AD平分∠BAC,DE⊥AB,∠C=90°, ∴DE=DC, ∵∠C=90°,∠BAC=60°, ∴∠B=30°, ∴DE=BD, ∴CD=BC=5, 故选:B. 17 14. 解:如图,过点P作PF⊥AD于F,作PG⊥BC于G, ∵AP是∠BAD的平分线,PE⊥AB, ∴PF=PE, 同理可得PG=PE, ∵AD∥BC, ∴点F、P、G三点共线, ∴FG的长即为AD、BC间的距离, ∴平行线AD与BC间的距离为3+3=6, 故选:D. 15. 解:(1)如图所示:过两把直尺的交点C作CE⊥AO,CF⊥BO, ∵两把完全相同的长方形直尺, ∴CE=CF, ∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上), 故选:A. 17 二.填空题(共5小题) 16. 解:如果一个点在角平分线上,那么它到角两边的距离相等. 17. 解:∵PM⊥OA,PN⊥OB,PM=PN, ∴∠AOC=∠BOC=20°, ∴∠AOB=40° 故答案为40°. 18. 解:作DE⊥AB于E, 由基本尺规作图可知,AD是△ABC的角平分线, ∵∠C=90°,DE⊥AB, ∴DE=DC=4, ∴△ABD的面积=×AB×DE=30, 故答案为:30. 17 19. 解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等. 故答案为:4 20. 解:作DF⊥AC于F, ∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC, ∴DF=DE=2, ∴△ADC的面积=×AC×DF=3, 故答案为:3. 三.解答题(共5小题) 21. 证明:设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F. ∵O是∠BAC角平分线AM上的一点(已知), ∴OE=OF(角平分线上的一点到这个角的两边的距离相等). 同理,OD=OF. ∴OD=OE(等量代换). ∵CP是∠ACB的平分线(已知), 17 ∴O在CP上(角的内部到角的两边距离相等的点在这个角的平分线上). 因此,AM,BN,CP交于一点; 故答案为:已知;角平分线上的一点到这个角的两边的距离相等;等量代换;已知;角的内部到角的两边距离相等的点在这个角的平分线上. 22. 解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC, ∴DE=DF, ∵S△ABC=28,AB=6,BC=8, ∴×6×DE+×8×DF=28, ∴7DE=28. ∴DE=4. 23. 证明:∵OM平分∠POQ,MA⊥OP,MB⊥OQ, ∴AM=BM, 在Rt△AOM和Rt△BOM中,, ∴Rt△AOM≌Rt△BOM(HL), ∴OA=OB, ∴∠OAB=∠OBA. 24. 证明:在Rt△BOF和Rt△COE中, , ∴Rt△BOF≌Rt△COE, ∴∠FBO=∠ECO, ∵OB=OC, ∴∠CBO=∠BCO, ∴∠ABC=∠ACB, 17 ∴AB=AC. 25. 证明:∵CD平分∠ACB, ∴∠1=∠2, ∵DE⊥AC,∠ABC=90° ∴DE=BD,∠3=∠4, ∵BF∥DE, ∴∠4=∠5, ∴∠3=∠5, ∴BD=BF, ∴DE=BF. 17查看更多