- 2021-02-27 发布 |
- 37.5 KB |
- 5页


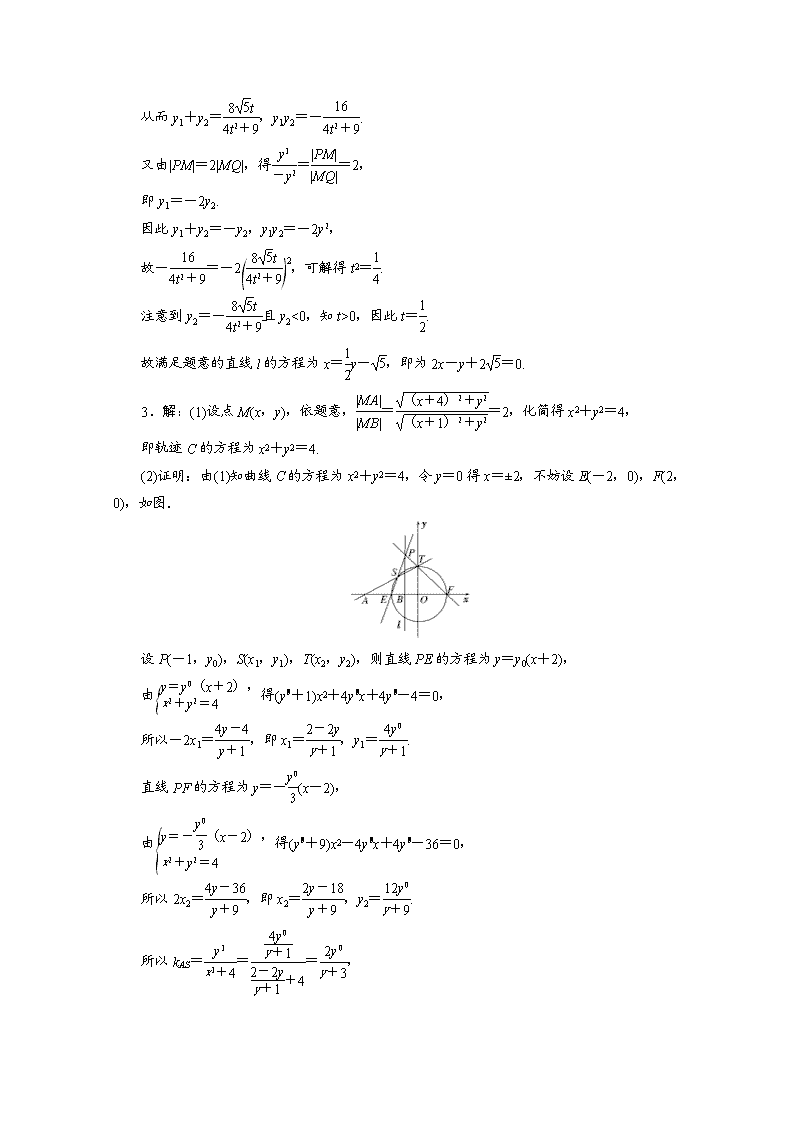
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【三维设计】2017届高三数学(理)二轮复习(通用版)课余自主加餐训练 (五)直线与圆锥曲线专练
(五)直线与圆锥曲线专练 1.过点Q(-2,)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4. (1)求r的值; (2)设P是圆O上位于第一象限内的任意一点,过点P作圆O的切线l,且l交x轴于点A,交y轴于点B,设,求||的最小值(O为坐标原点). 2.如图,F是椭圆+=1(a>b>0)的右焦点,O是坐标原点,|OF|=,过F作OF的垂线交椭圆于P0,Q0两点,△OP0Q0的面积为. (1)求该椭圆的标准方程; (2)若过点M(-,0)的直线l与上、下半椭圆分别交于点P,Q,且|PM|=2|MQ|,求直线l的方程. 3.已知点A(-4,0),直线l:x=-1与x轴交于点B,动点M到A,B两点的距离之比为2. (1)求点M的轨迹C的方程; (2)设C与x轴交于E,F两点,P是直线l上一点,且点P不在C上,直线PE,PF分别与C交于另一点S,T,证明:A,S,T三点共线. 4.(2016·四川高考)已知椭圆E:+=1(a>b>0)的 两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=-x+3与椭圆E有且只有一个公共点T. (1)求椭圆E的方程及点T的坐标; (2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值. 答 案 1.解:(1)由题可知,圆O的圆心为(0,0),半径为r. ∵过点Q(-2,)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4, ∴r=|OD|= ==3. (2)设直线l的方程为+=1(a>0,b>0), 即bx+ay-ab=0,则A(a,0),B(0,b), ∵, ∴=(a,b), ∴||=. ∵直线l与圆O相切,∴=3, ∴3=ab≤, ∴≥6,∴||≥6,当且仅当a=b=3时,等号成立. ∴||的最小值为6. 2.解:(1)由题设条件,|P0F|===. 易知|P0F|=, 从而=. 又c=|OF|=,即a2-b2=5, 因此a2-a-5=0, 解得a=3或a=-, 又a>0,故a=3,从而b=2. 故所求椭圆的标准方程为+=1. (2)设P(x1,y1),Q(x2,y2),由题意y1>0,y2<0,并可设直线l:x=ty-,代入椭圆方程得+=1,即(4t2+9)y2-8ty-16=0. 从而y1+y2=,y1y2=-. 又由|PM|=2|MQ|,得==2, 即y1=-2y2. 因此y1+y2=-y2,y1y2=-2y, 故-=-2,可解得t2=. 注意到y2=-且y2<0,知t>0,因此t=. 故满足题意的直线l的方程为x=y-,即为2x-y+2=0. 3.解:(1)设点M(x,y),依题意,==2,化简得x2+y2=4, 即轨迹C的方程为x2+y2=4. (2)证明:由(1)知曲线C的方程为x2+y2=4,令y=0得x=±2,不妨设E(-2,0),F(2,0),如图. 设P(-1,y0),S(x1,y1),T(x2,y2),则直线PE的方程为y=y0(x+2), 由得(y+1)x2+4yx+4y-4=0, 所以-2x1=,即x1=,y1=. 直线PF的方程为y=-(x-2), 由得(y+9)x2-4yx+4y-36=0, 所以2x2=,即x2=,y2=. 所以kAS===, kAT===, 所以kAS=kAT,所以A,S,T三点共线. 4.解:(1)由已知,a=b,则椭圆E的方程为+=1. 由方程组得3x2-12x+18-2b2=0. 由题意Δ=24(b2-3)=0,得b2=3, 则直线l与椭圆E的交点坐标为(2,1) 所以椭圆E的方程为+=1. 点T的坐标为(2,1). (2)证明:由已知可设直线l′的方程为y=x+m(m≠0), 由方程组可得 所以P点坐标为,|PT|2=m2. 设点A,B的坐标分别为A(x1,y1),B(x2,y2). 由方程组可得3x2+4mx+4m2-12=0. 由Δ=16(9-2m2)>0,解得-<m<. 则由根与系数的关系得x1+x2=-,x1x2=. 所以|PA|= =, 同理|PB|=. 所以|PA|·|PB|= = = =m2. 故存在常数λ=,使得|PT|2=λ|PA|·|PB|.查看更多