- 2021-02-26 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届内蒙古赤峰市宁城县高三10月月考(2017
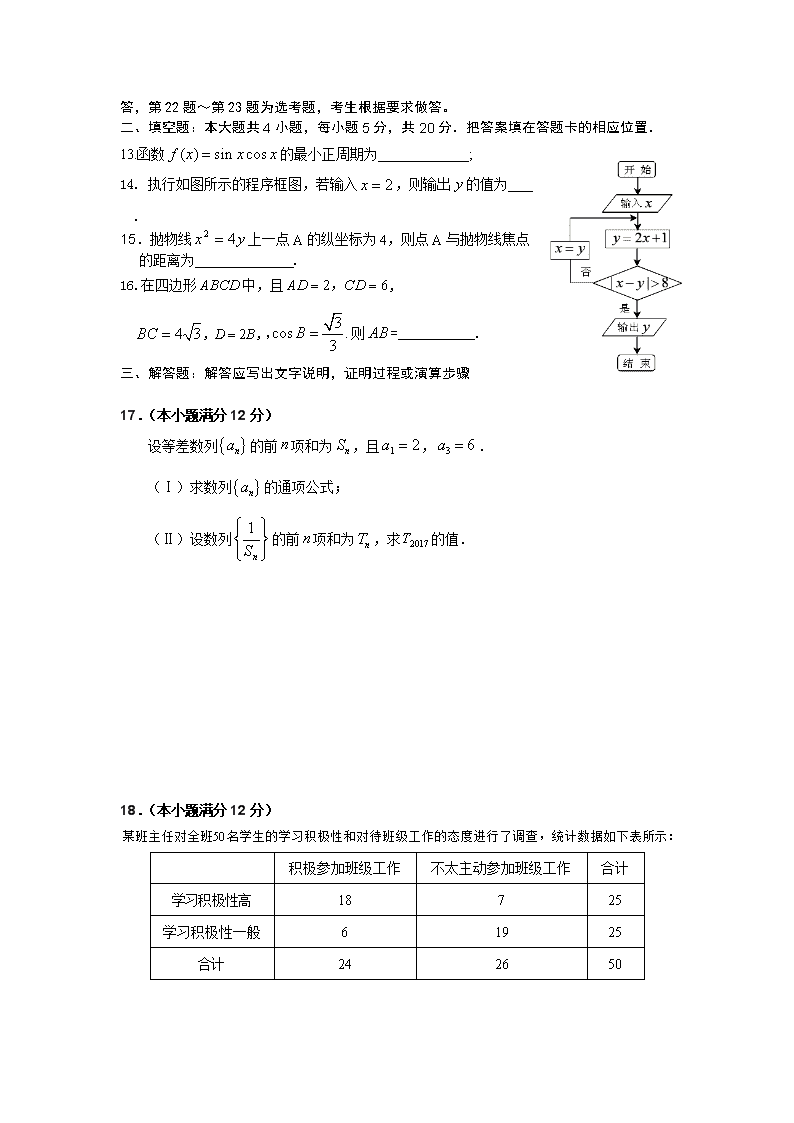
宁城县高三年级统一考试(2017.10.20) 数学试题(文科) 注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分 150 分,考试时间 120 分钟。答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应 位置上。 2.回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑。 如需改动,用橡皮擦干净后,再选涂其它答案标号。写在本试卷上无效。 3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。 4.考试结束后,将本试卷和答题卡一并交回。 第Ⅰ卷 一、选择题(本大题共 12 小题,每小题 5 分,满分 60 分.在每小题给出的四个选项中,只 有一项是符合题目要求的.) 1. 设集合 0 6A x x ,集合 2 2 8 0,B x x x x Z ,则 A B 错误! 未找到引用源。【来源:全,品…中&高*考+网】 (A) 4,2 错误!未找到引用源。 (B) 4 6 , 错误!未找到引用源。 ( C) 01, 错误!未找到引用源。 (D) 0,1,2 错误!未找到引用源。 2. i 是虚数单位,若复数 z 满足 1 3i i z ,则复数 z 的模是 (A) 2 (B) 2 (C) 4 (D) 3 3.某单位共有职工 150 名,其中高级职称 45 人,中级职称 90 人,初级职称 15 人,现采用 分层抽样方法从中抽取容量为 30 的样本,则各职称人数分别为 (A)9,16,5 (B) 10,15,5 (C) 10,17,3 (D)9,18,3 2 4 6log 3, log 3, log 3, , ,a b c a b c 4. 已知 则 的大小关系为 ( ) ( ) ( ) ( )A a b c B a c b C a b c D a c b 5.某路口的红绿灯,红灯时间为 30 秒,黄灯时间为 5 秒,绿灯时间为 40 秒,假设你在任 何时间到达该路口是等可能的,则当你到达该路口时,看见不是..黄灯的概率是 (A) 3 5 (B) 4 5 (C)14 15 (D) 1 15 6. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难, 次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一 个人走 378 里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了 6 天后到达目的地,请问第三天走了 (A)96 里 (B)48 里 (C) 192 里 (D)24 里 7.某空间几何体的三视图如图所示(图中小正方形的边长为 1), 则这个几何体的外接球的面积是 (A)36 (B)16 (C) 48 (D)32 3 8.若实数 x , y 满足不等式组 1, 2, 0, y x y x y 则 yxz 2 的最小值为 (A)1 (B) 2 (C) 2 5 (D) 2 7 9. 2 | | 2 3( ) ( ) ( ) ( )6 4 3 4 a b a b a a b A B C D 已知 , , ,则 , 10.若双曲线 2 2 2 2 1( 0, 0)x y a ba b 的一条渐近线与圆 2 2( 3) ( 1) 3x y 相切,则 此双曲线的离心率为 (A)2 (B) 7 2 (C) 2 3 3 (D) 7 11.函数 y= x xa x (a>1)的图象的大致形状是 (A) (B) (C) (D) 12.已知函数 21 ,f x g x xx .若直线 l 与曲线 ,f x g x 都相切,则直线 l 的方程为 (A) 2 4 0x y (B) 2 4 0x y (C) 4 4 0x y (D) 4 4 0x y 宁城县高三年级统一考试(2017.10.20) 数学试题(文科) 第Ⅱ卷(非选择题共 90 分) 本卷包括必考题和选考题两部分,第 13 题~第 21 题为必考题,每个试题考生都必须做 答,第 22 题~第 23 题为选考题,考生根据要求做答。 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.把答案填在答题卡的相应位置. 13.函数 ( ) sin cosf x x x 的最小正周期为_____________; 14. 执行如图所示的程序框图,若输入 2x ,则输出 y 的值 为 . 15.抛物线 yx 42 上一点 A 的纵坐标为 4,则点 A 与抛物线焦点 的距离为 . 16.在四边形 ABCD 中,且 2 6AD CD , , 4 3BC , 2D B , 3cos .3B , 则 AB =___________. 三、解答题:解答应写出文字说明,证明过程或演算步骤 17.(本小题满分 12 分) 设等差数列 na 的前 n 项和为 nS ,且 1 2a , 3 6a . (Ⅰ)求数列 na 的通项公式; (Ⅱ)设数列 1 nS 的前 n 项和为 nT ,求 2017T 的值. 18.(本小题满分 12 分) 50某班主任对全班 名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示: 积极参加班级工作 不太主动参加班级工作 合计 学习积极性高 18 7 25 学习积极性一般 6 19 25 合计 24 26 50 2 2 0,1 n ad bcK a b c d a c b d Ⅰ 按照分层抽样从积极参加班级工作中抽取4人,再从这4人中任选2人参加某项活动,求这两人 学习积极性都高的概率; Ⅱ 试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作态度是否有关? 并说明理由. 参考公式与临界值表: 【来源:全,品…中&高*考+网】 19.(本小题满分 12 分) 1 1 1 1 1 1 1 1 1 1 1 - 2 , 1 .3 ABC A B C ABB A ABB A BCC B BCC BC D CC 在三棱柱 中,四边形 是边长为 的正方形,且平面 平面 , , 为 中点 [ 1 1 1 .. DB ABDⅠ 证明: 平面 ; Ⅱ 求A 到平面AB D的距离 【来源:全,品…中&高*考+网】 20.(本小题满分 12 分) 在平面直角坐标系 xoy 中,点 1 3,0F ,圆 F2: 2 2 2 3 13 0x y x ,以动点 P 为圆心的圆过点 F1,且圆 P 与圆 F2 内切. (Ⅰ)求动点的轨迹 C 的方程; (Ⅱ)设过点 1F 的直线 l 和(Ⅰ)中轨迹 C 椭圆交于两点 ,A B ,且 1 12AF F B ,求直 线l 的方程. 2P K k 0.100 0.050 0.025 [来 0.010 0.001 k 2.706 3.841 5.024 6.635 10.828 【来源:全,品…中&高*考+网】 21.(本小题满分 12 分) 已知函数 2ln 1 ,f x x a x 其中 0.a Ⅰ 当 2a 时,求函数 f x 的单调性; Ⅱ 若函数 f x 有两个极值点 1 2, ,x x 且 1 2 ,x x 求证: 2 1 -ln 2 0.2 f x 【来源:全,品…中&高*考+网】 请考生在第 22、23 二题中任选一题做答,如果多做,则按所做的第一题记分,做答时 请写清题号) 22.(本小题满分 10 分)选修 4—4:坐标系与参数方程 以坐标原点 为极点,以 轴正半轴为极轴,建立极坐标系,已知曲线 C 的极坐标方程为 cos 2sin 10 ,将曲线 1 cos: sin xC y ( 为参数),经过伸缩变换 / / 3 2 x x y y 后 得到曲线 2C . (Ⅰ)求曲线 2C 的参数方程; (Ⅱ)若点 M 的曲线 2C 上运动,试求出 M 到直线 C 的距离的最小值. 23.(本小题满分 10 分)选修 4-5:不等式选讲 已知函数 1 1( ) 2 2f x x x 的最小值为 m . (Ⅰ)求 m ; (Ⅱ)若 , , ,a b c d R 且 2 2 2 2a b c d m ,证明: 1ac bd . 宁城县高三年级统一考试(2017.10.20) 数学试题(文科)参考答案 一、 选择题:DADA CBCD BCCD 二、 填空题:13、 ; 14、23; 15、5; 16、8。 三、 解答题 17. 解:(1) 公差 ,-----------------2 分 通项公式 ,即 -----------5 分 (2) ,------------------7 分 所以 --------------------------9 分 ---------------12 分 20.解:(1)圆 F2: 化为 . 故 ,半径 r=4.而 <4, ∴点 F1 在圆 F2 内, 又由已知得圆 P 的半径 R=|PF1|,由圆 P 与圆 F2 内切得,圆 P 内切于圆 F2, 即|PF2|=4﹣|PF1|,∴|PF1|+|PF2|=4>|F1F2|,-------------------------------4 分 故点 P 的轨迹是以 F1、F2 为焦点,长轴长为 4 的椭圆, 有 ,则 . 故动点的轨迹方程为 ;---------------------------5 分 (2)设直线 的方程是 由 消 并整理得 ------------------8 分 显然 设 , ,则 ①, ② -------10 分 因为 得 ③, 由①②③解得 , 即 因此存在直线 : , 使得 --------------------12 分 21.解: ------2 分 当 时, ,即时,令 得 --------------4 分 的单调递增区间是 和 ,单调递减区间是 ………5 分 证明: 在 单调递增,且 , ,…….6 分 有两个极值点 , . ---------------------7 分 令 ---------------9 分 在 单调递增. 【来源:全,品…中&高*考+网】 ------------------------11 分 综上可知: ……………………………………….12 分 22. 解(1)将曲线 ( 为参数)化为 ,【来源:全,品…中&高* 考+网】 由伸缩变换 化为 ,代入圆的方程得 , 可得曲线 的参数方程为 ( 为参数).-----------------5 分 (2)曲线 的极坐标方程 ,化为直角坐标方程: , 设 点 到 的距离 ,【来源:全,品…中&高*考+网】 ∴点 到 的距离的最小值为 .---------------------------10 分 解:(1) ∴ --------------------------5 分 (2)∵ ∴ -----------8 分 ∵ ∴ --------------------10 分查看更多