- 2021-02-26 发布 |
- 37.5 KB |
- 14页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全国各地高考模拟数学试题汇编空间几何体的三视图表面积与体积理卷A
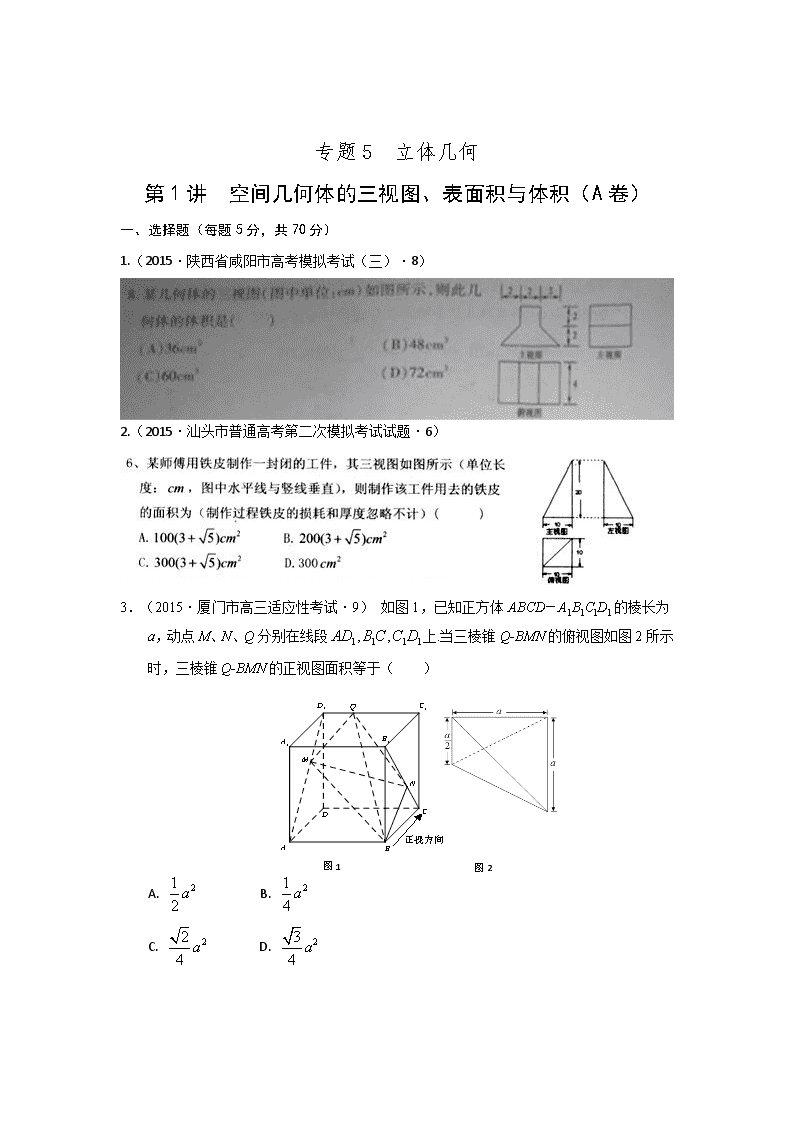
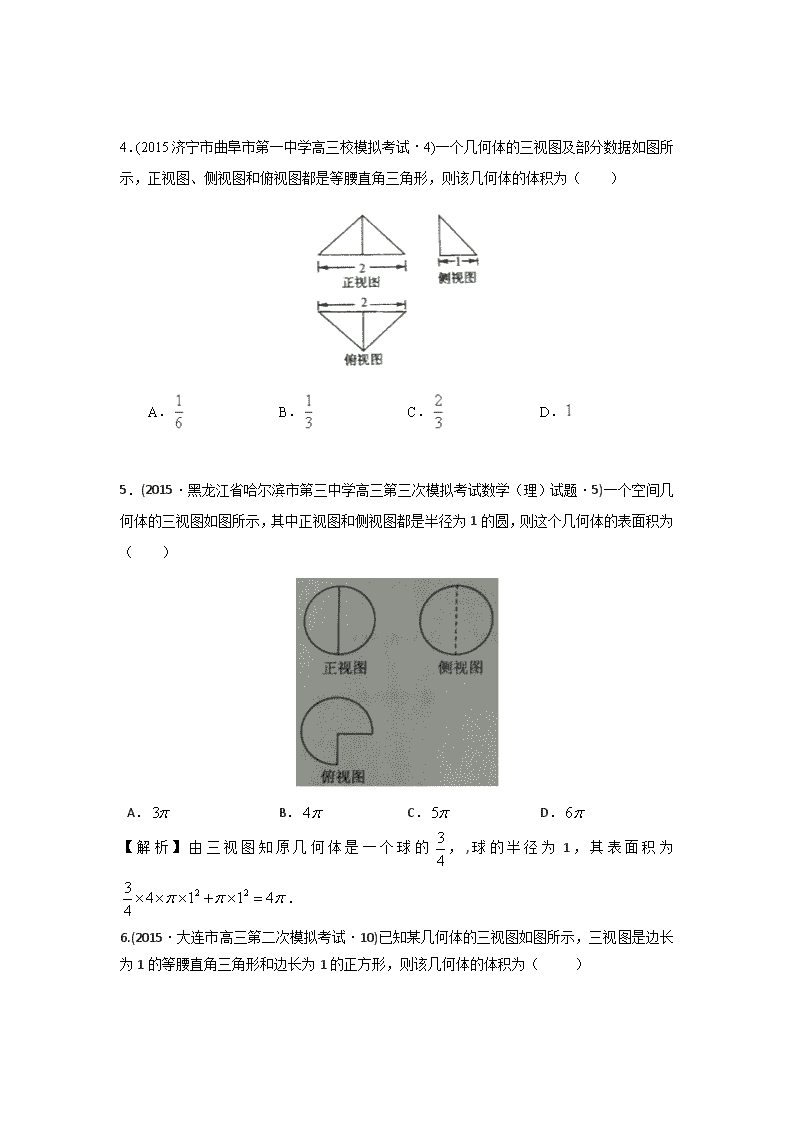
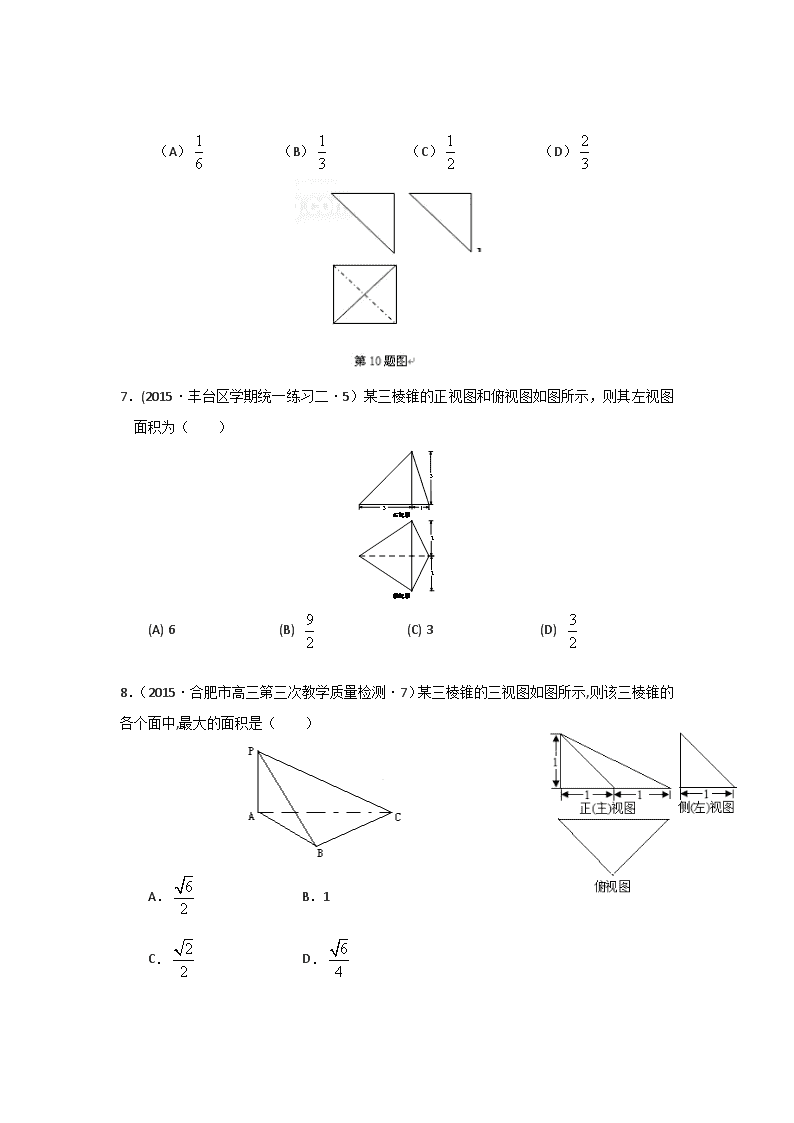
专题5 立体几何 第1讲 空间几何体的三视图、表面积与体积(A卷) 一、选择题(每题5分,共70分) 1.(2015·陕西省咸阳市高考模拟考试(三)·8) 2.(2015·汕头市普通高考第二次模拟考试试题·6) 3.(2015·厦门市高三适应性考试·9) 如图1,已知正方体ABCD-A1B1ClD1的棱长为a,动点M、N、Q分别在线段上.当三棱锥Q-BMN的俯视图如图2所示时,三棱锥Q-BMN的正视图面积等于( ) 正视方向 图1 图2 A. B. C. D. 4.(2015济宁市曲阜市第一中学高三校模拟考试·4)一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的体积为( ) A. B. C. D. 5.(2015·黑龙江省哈尔滨市第三中学高三第三次模拟考试数学(理)试题·5)一个空间几何体的三视图如图所示,其中正视图和侧视图都是半径为1的圆,则这个几何体的表面积为( ) A. B. C. D. 【解析】由三视图知原几何体是一个球的,,球的半径为1,其表面积为. 6.(2015·大连市高三第二次模拟考试·10)已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为( ) (A) (B) (C) (D) 7.(2015·丰台区学期统一练习二·5)某三棱锥的正视图和俯视图如图所示,则其左视图面积为( ) (A) 6 (B) (C) 3 (D) 8.(2015·合肥市高三第三次教学质量检测·7)某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是( ) A. B.1 C. D. 9.(2015·开封市高三数学(理)冲刺模拟考试·5)某几何体的三视图如下图所示,则该几何体的体积为( ) A.12 B.24 C.30 D.48 10.(2015·开封市高三数学(理)冲刺模拟考试·11)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( ) A. B. C. D. 11. (2015·哈尔滨市第六中学高三第三次模拟考试·9) 如图,一个空间几何体的正视图、侧视图都是面积为,一个内角为 的菱形,俯视图为正方形,那么这个几何体的表面积为( ) A. B. C. D. 12.(2015·河北省唐山市高三第三次模拟考试·8) 13.(2015·山东省潍坊市高三第二次模拟考试·7) 已知三棱锥S—ABC的所有顶点都在球O的球面上,底面△ABC是边长为1的正三角形,棱SC是球O的直径且SC=2,则此三棱锥的体积为( ) A. B. C. D. 14.(江西省九江市2015届高三第三次模拟考试·5)已知某锥体的正视图和侧视图如图所示,其体积为,则该锥体的俯视图可以是( ) 二、非选择题(30分) 15.(2015·日照市高三校际联合5月检测·13)若某几何体的三视图如右图所示,则此几何体的体积是______. . 16. (2015·济宁市5月高考模拟考试·14) 17. (江西省九江市2015届高三第三次模拟考试·15)已知点A、B、C、D在同一球面上,且,若四面体ABCD体积的最大值为,则该球的表面积为 18、(2015·海南省高考模拟测试题·15)某几何体的三视图如图所示,则此几何体的对应直观图中的面积为__________. 19 (2015·哈尔滨市第六中学高三第三次模拟考试·15)已知球的直径,是球球面上的三点,, 是正三角形,则三棱锥的体积为 . 20. (2015·济南市高三教学质量调研考试·15)如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是_________cm. 专题5 立体几何 第1讲 空间几何体的三视图、表面积与体积(A卷)答案与解析 1.【答案】 B. 【命题立意】考查立体几何中三视图的观察与应用,以及简单几何体体积的计算. 【解析】由于从三视图可以看出几何体的上半部分是截面为正方形的直四棱柱,下半部分是截面为等腰梯形的直四棱柱,所以其体积为.故选B. 2.【答案】A 【命题立意】本题考查的知识点是三视图和几何体的表面积. 【解析】由三视图可知,该几何体的形状如图,它是底面为正方形,各个侧面均为直角三角形的四棱锥,用去的铁皮的面积即该棱锥的表面积,其底面边长为10,故底面面积为10×10=100 与底面垂直的两个侧面是全等的直角,两直角连年长度分别为10,20,故它们的面积皆为100 另两个侧面也是全等的直角三角形,两直角边中一边是底面正方形的边长10,另一边可在与底面垂直的直角三角形中求得,其长为,故此两侧面的面积皆为故此四棱锥的表面积为S=100(3+)cm2. 故选A. 3.【答案】B 【命题立意】本题旨在考查几何体的三视图. 【解析】由俯视图可知点N和点C重合,Q点和重合,M为的中点,故其正视图为三角形,如图: 从而得到其面积为:.故选:B 4.【答案】B 【命题立意】本题考查的知识点是由三视图求体积,其中根据三视图判断出几何体的形状,分析出几何体的几何特征,进而求出底面面积,高是解答本题的关键. 【解析】由三视图判断几何体为三棱锥,如图:由已知中侧视图是一个等腰直角三角形,宽为1,∴棱锥的高H=1;底面△的高也为1,又由俯视图为等腰直角三角形,且底面斜边长为2,∴底面面积S=×2×1=1,则几何体的体积V=×1×1=. 5.【答案】B 【命题立意】考查三视图,考查空间想象能力,容易题. 6.【答案】A 【命题立意】本题重点考查了三视图、空间几何体的结构特征等知识。 【解析】通过三视图,可以看到该几何体为一个四棱锥,底面为边长为1,其体积为。 7.【答案】C 【命题立意】考查三视图,考查空间想象能力,容易题. 【解析】依题意,三棱锥的左视图为. 8.【答案】A 【命题立意】本题重点考查空间几何体的三视图和线面垂直的判定,难度中等. 【解析】该几何体的三视图如图所示,由三视图可知,所以该三棱锥的各个面中,最大的面积是,其面积为. 9.【答案】B 【命题立意】本题旨在考查空间几何体的三视图与体积. 【解析】根据三视图可得该几何体是一个如图所示的几何体,可分解为上面是一个四棱锥,下面是一个三棱柱,则其体积为V=×4×3×2+×3×3×4=24. 10.【答案】A 【命题立意】本题旨在考查三棱锥的外接球的体积. 【解析】由于∠DAB=60°,则三棱锥P—DCE各边长度均为1,那么三棱锥P—DCE为正三棱锥,P点在底面DCE的投影为等边△DCE的中心,设中心为O,则有OD=OE=OC=,在直角△POD中,OP2=PD2-OD2=,即OP= ,由于外接球的球心必在OP上,设球心位置为O1,则O1P=O1D,设O1P=O1D=R,则在直角△OO1D中,OO12+OD2=O1D2,则(OP-O1P)2+OD2=O1D2,即(-R)2+()2=R2,解得R=,故三棱锥P—DCE的外接球的体积为V=πR3=π. 11.【答案】D 【命题立意】本题旨在考查几何体的三视图及表面积。 【解析】(1)该图上部是一个正四棱锥,下部是倒的正四棱锥,两个正四棱锥关于中间的底面对称. (2)面积为,且一个内角为60°的棱形,其边长是1,一条对角线长是1,另一条对角线长是根号 (3)正四棱锥的底面是边长为1的正方形,4 个侧面是同一样的底边长为1、底边上高为1的等腰三角形.这个几何体的表面积=8个底边长为1、底边上高为1的等腰三角形和 . 12.【答案】A 【命题立意】本题重点考查空间几何体的三视图和球、锥的体积公式,难度中等. 【解析】由三视图可知该几何体上面是一个半径为1的半球,下面是一个底面积为2,高为1的正四棱锥,所以其体积为. 13.【答案】A 【命题立意】本题旨在考查通过三棱锥和球的组合,求得三棱锥的体积 【解析】取正三角形ABC的中心,连接又因为 ., 所以. 14.【答案】C 【命题立意】本题旨在考查三视图及其应用、锥体的体积公式等知识。 【解析】结合其锥体的体积,得到只有C符合题意,故选C。 15.【答案】 【命题立意】本题旨在考查三视图与几何体体积. 【解析】由图知此几何体为边长为2的 正方体裁去一个三棱锥(如右图),所以此几何体的体积为 16.【答案】 【命题立意】本题主要考查空间几何体的三视图、外接球的半径的求解及球的表面积公式 【解析】由三视图所给数据可得在该几何体的棱的一半、外接球的半径与底面所在圆的半径所构成的直角三角形中求得外接球的半径的平方为,故外接球的表面积为. 17.【答案】9 【命题立意】本题旨在考查四面体的结构特征、球的表面积公式、四面体的体积等知识。 【解析】因为,故为直角三角形,当点D到平面ABC的距离最大时,其四面体的体积最大,也就是点D在平面ABC内的射影恰为斜边中点时,体积最大,故得到其球的半径为,故其体积为。 18.【答案】 【命题立意】本题旨在考查空间几何体的三视图及其应用. 【解析】根据三视图知该几何体的底面是边长为2的等边三角形,同时侧棱PC⊥底面ABC,则有PA=PB=2,而AB=2,那么△PAB中边AB上的高为,则对应的面积为S=×2×=. 19.【答案】 【命题立意】本题旨在考查球及三棱锥。 【解析】设球心为M,三角形ABC截面小圆的圆心为0,∵ABC是等边三角形,∠APQ=∠BPQ=∠CPQ=30°∴P在面ABC的投影O是等边△ABC的重心(此时四心合一)∵PQ是直径, ∴∠PCQ=90°.∴PC=4cos30°= ∴PO=cos30°=3. OC=sin30°= O是等边△ABC的重心∴OC= OH∴等边三角形ABC的高OH= , AC= sin60°=3.三棱锥P-ABC体积= PO•S△ABC= 20.【答案】 【命题立意】本题旨在考查 柱、锥、台、球的结构特征 . 【解析】依题意可得碗的球心为O,半径为R.其它三个球的球心分别是.这四个点构成了一个正三棱锥,其中侧棱表示两个球内切的圆心距关系.底面长为两个外切求的圆心距.所以="R-5."O1O2=10.通过解直角三角形可得R=.故填. 查看更多