数学文卷·2018届江西省南昌市高三第一次模拟考试（2018

数学文卷·2018届江西省南昌市高三第一次模拟考试（2018

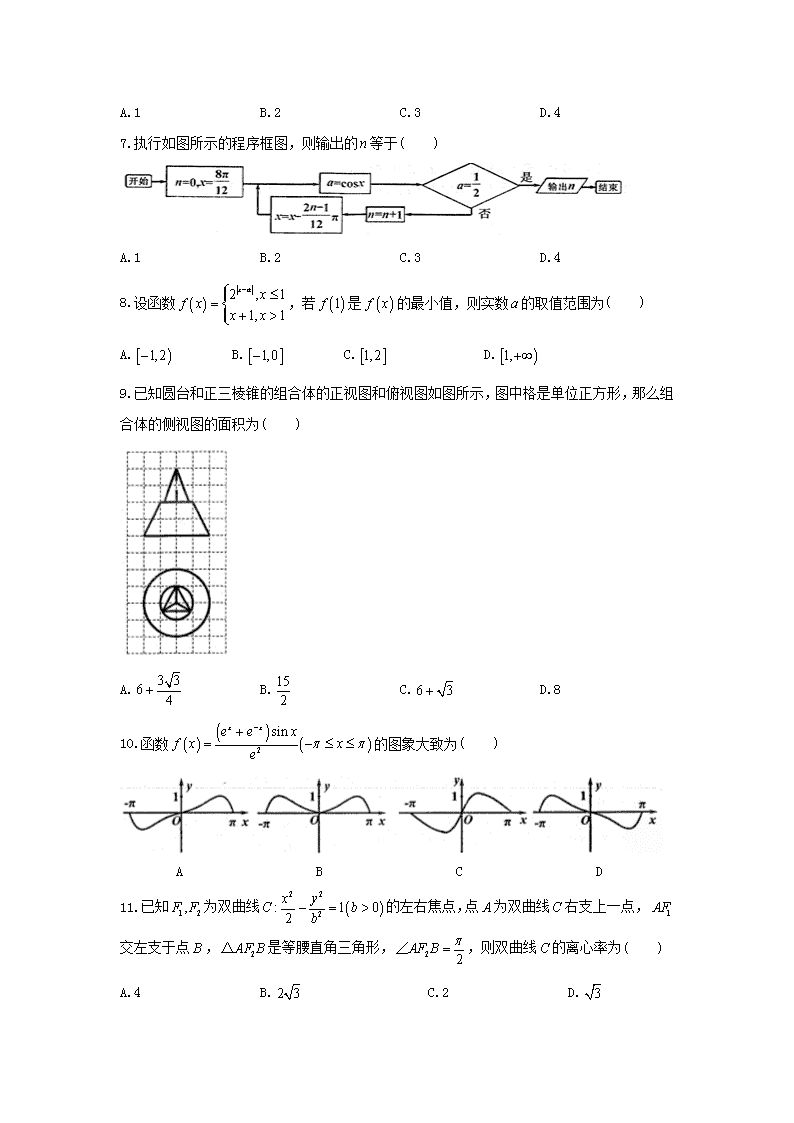
江西省南昌市 2018 届高三第一次模拟考试 文科数学 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中，只有一项是符合题目要求的. 1.已知集合 ， ，则 ( ) A. B. C. D. 2.欧拉公式 ( 为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函 数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常重要， 被誉为“数学中的天桥”，根据欧拉公式可知， 表示的复数位于复平面中的( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.已知 是定义在 上的偶函数，且 在 上单调递增，则( ) A. B. C. D. 4.已知 ， ，那么 是 成立的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不 必要条件 5.设不等式组 表示的平面区域为 ，若直线 经过区域 内的点，则实 数 的取值范围为( ) A. B. C. D. 6.已知函数 的部分图象如图所示，则 的值可以为( ) { }4A x N y x= ∈ = − { }2 1,B x x n n Z= = + ∈ A B = ( ],4−∞ { }1,3 { }1,3,5 [ ]1,3 cos sinixe x i x= + i 3 i e π ( )f x R ( )f x ( )0,+∞ ( ) ( ) ( )3 20 log 2 log 3f f f> > − ( ) ( ) ( )3 2log 2 0 log 3f f f> > − ( ) ( ) ( )2 3log 3 log 2 0f f f− > > ( ) ( ) ( )2 3log 3 0 log 2f f f− > > 0a > b R∈ 0a b+ > a b> 3 0 1 0 3 5 0 x y x y x y + − ≥  − + ≥  − − ≤ M y kx= M k 1 ,22      1 4,2 3      1 ,22      4 ,23      ( ) ( )2sin 06f x x πω ω = − >   ω A.1 B.2 C.3 D.4 7.执行如图所示的程序框图，则输出的 等于( ) A.1 B.2 C.3 D.4 8.设函数 ，若 是 的最小值，则实数 的取值范围为( ) A. B. C. D. 9.已知圆台和正三棱锥的组合体的正视图和俯视图如图所示，图中格是单位正方形，那么组 合体的侧视图的面积为( ) A. B. C. D.8 10.函数 的图象大致为( ) A B C D 11.已知 为双曲线 的左右焦点，点 为双曲线 右支上一点， 交左支于点 ， 是等腰直角三角形， ，则双曲线 的离心率为( ) A.4 B. C.2 D. n ( ) 2 , 1 1, 1 x a xf x x x − ≤=  + > ( )1f ( )f x a [ )1,2− [ ]1,0− [ ]1,2 [ )1,+∞ 3 36 4 + 15 2 6 3+ ( ) ( ) ( )2 sinx xe e x f x xe π π −+ = − ≤ ≤ 1 2,F F ( )2 2 2: 1 02 x yC bb − = > A C 1AF B 2AF B△ 2 2AF B π=∠ C 2 3 3 12.已知台风中心位于城市 东偏北 ( 为锐角)度的 200 公里处，以 公里/小时沿正西方 向快速移动， 小时后到达距城市 西偏北 ( 为锐角)度的 200 公里处，若 ，则 ( ) A. B.80 C.100 D.125 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13.设函数 在 内可导，其导函数为 ，且 ，则 ____________. 14.已知平面向量 ， ，若 ，则实数 ____________. 15.在圆 上任取一点，则该点到直线 的距离 的概率为 ____________. 16.已知函数 ，若 ， ，且 ，则 ________. 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演 算步骤.） 17.已知等比数列 的前 项和为 ，满足 ， . (1)求 的通项公式； (2)记 ，求 的最大值. 18.某校为了推动数学教学方法的改革，学校将高一年级部分生源情况基本相同的学生分成 甲、乙两个班，每班各 40 人，甲班按原有模式教学，乙班实施教学方法改革.经过一年的教 学实验，将甲、乙两个班学生一年来的数学成绩取平均数再取整，绘制成如下茎叶图，规定 不低于 85 分(百分制)为优秀，甲班同学成绩的中位数为 74. (1) 求 的值和乙班同学成绩的众数； A α α v 2.5 A β β 3cos cos4 α β= v = 60 ( )f x ( )0,+∞ ( )'f x ( )ln lnf x x x= + ( )' 1f = ( )1,a m= ( )4,b m= ( ) ( )2 0a b a b− ⋅ + =    m = 2 2 4x y+ = 2 2 0x y+ − = [ ]0,1d ∈ ( ) 3 sinf x x x= + [ ]0,α π∈ ,4 4 π πβ  ∈ −   ( )22f f π α β − =   cos 2 α β + =   { }na n nS 4 42 1S a= − 3 32 1S a= − { }na 2 16log 1n n b S  =  +  1 2 nb b b+ + +… x (2) 完成表格，若有 以上的把握认为“数学成绩优秀与教学改革有关”的话，那么学 校将扩大教学改革面，请问学校是否要扩大改革面？说明理由. 19. 如图，四棱锥 中， 底面 ， 为直角梯形， 与 相交于 点 ， ， ， ，三棱锥 的体积为 9. (1)求 的值； (2)过 点的平面 平行于平面 ， 与棱 ， ， ， 分别相交于点 ，求截面 的周长. 20.已知椭圆 的下顶点为 ，右顶点为 ，离心率 ，抛物线 的焦点为 ， 是抛物线 上一点，抛物线 在点 处的切线为 ，且 . (1)求直线 的方程； (2)若 与椭圆 相交于 ， 两点，且 ，求 的方程. 21.已知函数 ，其中 为自然对数的底数. (1)若 在 处取到极小值，求 的值及函数 的单调区间； (2)若当 时， 恒成立，求 的取值范围. 22.在平面直角坐标系 中，曲线 的参数方程为 ( 为参数)，以坐标原点 为极点， 轴非负半轴为极轴建立极坐标系. (1)求 的极坐标方程； 90% P ABCD− PA ⊥ ABCD ABCD AC BD O AD BC∥ AD AB⊥ 3AB BC AP= = = P ACD− AD O α PAB α BC AD PD PC , , ,E F G H EFGH ( )2 2 2 2: 1 0x yC a ba b + = > > A B 3 2e = 2 : 8 xE y = F P E E P l l AB∥ l l C M N 5 31 4FMNS =△ C ( ) ( )lnxf x e a x e a= − − ∈R e ( )f x 1x = a ( )f x [ )1,x∈ +∞ ( )f x 0≥ a xOy C 2cos 2sin 2 x y θ θ =  = + θ x C (2)若直线 的极坐标方程分别为 ， ，设直线 与曲线 的 交点为 ， ， ，求 的面积. 23.已知 . (1)当 时，求不等式 的解集； (2)对于任意实数 ，不等式 成立，求实数 的取值范围. 1 2,l l ( ) 6 R πθ ρ= ∈ ( )2= 3 R πθ ρ ∈ 1 2,l l C O M N OMN△ ( ) 22 3f x x a= + 0a = ( ) 2 3f x x+ − ≥ x ( )2 1 2x f x a+ − < a 804040 61 19 27 13 34 6 乙班甲班 合计 合计 不优秀人数 优秀人数 M N O D CB A P E F G H NCS20180607 项目第一次模拟测试卷 文科数学参考答案及评分标准 一.选择题：本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只 有一项是符合题目要求的． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A C B C B B C B A D C 二.填空题:本大题共 4 小题,每小题 5 分，满分 20 分． 13． 14. 15. 16. 三.解答题：本大题共 6 小题，共 70 分，解答应写出文字说明，证明过程或推演步骤. 17.【解析】（Ⅰ）设 的公比为 ，由 得， , 所以 ， 所以 . 又因为 所以 ， 所以 . 所以 . （ Ⅱ ） 由 （ Ⅰ ） 知 ， ， 所 以 ， ，所以 是首项为 ，公差为 的等差数列， 所以 当 时 ， 所以当 或 时， 的最大值为 . 18. 【解析】（Ⅰ）由甲班同学成绩的中位数为 ， 所以 ，得 由茎叶图知，乙班同学成绩的众数为 （Ⅱ）依题意知 （表格 2 分， 计算 4 分） 有 90%以上的把握认为“数学成绩优秀与教学改革有关”，学校可以扩大教学改革面. 19. 【解析】（Ⅰ）四棱锥 中， 底面 ， 为直角梯形， ， ， 所以 ，解得 . （Ⅱ）【法一】因为 平面 ，平面 平面 ， ， 平面 平面 ， 根据面面平行的性质定理，所以 ， 同理 , 因为 , 所以 ∽ ，且 ， 又因为 ∽ ， ,所以 ， 同理 , ， 如 图 ： 作 , 所 以 e+1 5± 1 3 2 2 { }na q 4 3 4S S a- = 4 3 42 2a a a- = 4 3 2a a = 2q = 3 32 1S a= - 1 1 1 12 4 8 1a a a a+ + = - 1 1a = 12n na -= 1 2 2 11 2 n n nS -= = -- 4 22 16log ( ) 2log 2 8 21 n n n b nS -= = = -+ 1 2n nb b −− = − { }nb 6 2− 1 2 3 46, 4, 2, 0,b b b b= = = = 5n > 0nb < 3n = 4n = 1 2 nb b b+ + + 12 74 7 75 2 74x + = × 3x = 78,83 2 2 80 (6 27 13 34) 3.382 2.70640 40 19 61K × × − ×= ≈ >× × × 2K P ABCD- PA ^ ABCD ABCD // ,AD BC AD AB^ 3AB BC AP= = = 1 3 93 2 2P ACD AB AD ADV AP- ×= ´ × = = 6AD = //a PAB a  ABCD EF= O EFÎ PAB  ABCD AB= //EF AB // , //EH BP FG AP // , 2BC AD AD BC= BOCD DOAD 1 2 BC CO AD OA= = COED AOFD AF BE= 2BE EC= 2AF FD= 2PG GD= 1 23, 2, 23 3EF AB EH PB FG AP= = = = = = // , , // ,HN BC HN PB N GM AD GM PA M= =  E N O H C D B A F G P ， 故四边形 为矩形，即 ， （求 长 2 分，其余三边各 1 分） 在 中，所以 所以截面 的周长为 . 【法二】因为 平面 ，平面 平面 ， ，平面 平面 ， 所以 ，同理 因为 ∥ 所以 ∽ ，且 ， 所以 ， 同理 ，连接 ，则有 ∥ ， 所以 ， ，所以 ，同理， ， 过点 作 ∥ 交 于 ，则 ， 所以截面 的周长为 . 20. 【解析】（Ⅰ）因为 ， 所以 ， 所以 又因为 ∥ ， 所以 的斜率为 设 ，过点 与 相切的直线 ，由 得 ，解得 所以 ， 所以直线 的方程为 （Ⅱ）设 ，由 得 ， ， 且 ，即 ， 所以 ， 【法一】 中，令 得 ， 交 轴于 , 又抛物线焦点 ，所以 所以 ，解得 ， // ,HN GM HN GM= GMNH GH MN= GH PMND 8 1 2 2 2 cos45 5MN °= + - ´ ´ = EFGH 3 2 5 2 5 5 2+ + + = + + //a PAB a  ABCD EF= O EFÎ PAB  ABCD AB= //EF AB // , //EH BP FG AP BC , 6, 3AD AD BC= = BOCD DOAD 1 2 BC CO AD AO= = 1 2 EO OF = 1 1, 23CE CB BE AF= = = = 1 3 CH EH CO PC PB CA= = = HO HO PA HO EO⊥ 1HO = 1 23EH PB= = 2 23FG PA= = H HN EF FG N 2 2 5GH HN GN= + = EFGH 3 2 5 2 5 5 2+ + + = + + 2 2 2 31 4 be a = − = 1 2 b a = 1 2ABk = l AB l 1 2 2 ( , )8 tP t P E l 2 8 xy = 1' |4 4 2x t x ty == = = 2t = 1(2, )2P l 2 1 0x y− − = ),(),,( 2211 yxNyxM 2 2 2 2 14 1 2 x y b b xy  + = − = 2 22 2 1 4 0x x b− + − = 2 1 2 1 2 1 41, 2 bx x x x −+ = = 24 8(1 4 ) 0bD = - - > 2 1 8b > 2 2 1 2 1 2 1 2| | ( ) 4 8 1x x x x x x b− = + − = − : 2 1 0l x y− − = 0x = 1 2y = − l y D (0,2)F 1 5| | 2 2 2FD = + = 2 1 2 1 1 5 5 31| | | | 8 12 2 2 4FMNS FD x x b∆ = ⋅ − = × − = 2 4b = 所以椭圆 的方程 【法二】 ，抛物线焦点 ，则 所以 ，解得 ， 所以椭圆 的方程 21. 【解析】（Ⅰ）由 ，得 因为 ，所以 ，所以 令 ，则 ， 当 时， ，故 在 单调递增，且 所以当 ， . 即当 时， ，当 时， . 所以函数 在 上递减，在 上递增. （Ⅱ）【法一】由 ，得 （1）当 时， ， 在 上递增 （合题意） （2）当 时， ，当 时， ①当 时，因为 ，所以 ， . 在 上递增， （合题意） ②当 时，存在 时，满足 在 上递减， 上递增，故 . 不满足 时， 恒成立 综上所述， 的取值范围是 . 【法二】由 ，发现 由 在 恒成立，知其成立的必要条件是 而 ， ，即 ①当 时， 恒成立，此时 在 上单调递增， （合题意）. C 2 2 1.16 4 x y+ = 2 1 2 1 5| | 1 | | 8 14 2MN x x b= + − = − : 2 1 0l x y− − = (0,2)F | 0 4 1| 5 5F ld ® - -= = 21 1 5 5 31| | 8 1 52 2 2 4FMN F lS MN d b∆ →= ⋅ = × − × = 2 4b = C 2 2 1.16 4 x y+ = ( ) e ln e( R)xf x a x a= - - Î ( ) ex af x x¢ = - (1) 0f ¢ = ea = e e e( ) e x x xf x x x -¢ = - = ( ) e exg x x= - ( ) e (1 )xg x x¢ = + 0x > ( ) 0g x¢ > ( )g x (0, )x Î +¥ (1) 0,g = (0,1) , ( ) 0x g xÎ <时 (1, ) , ( ) 0x g xÎ +¥ >时 (0,1)x Î '( ) 0f x < (1, )x Î +¥ '( ) 0f x > ( )f x (0,1) (1, )+¥ ( ) e ln exf x a x= - - ( ) ex af x x¢ = - 0a £ ( ) e 0x af x x¢ = - > ( )f x [1, )x Î +¥ min( ) (1) 0f x f= = 0a > ( ) e 0x af x x¢ = - = [1, )x Î +¥ e exy = ³ (0,e]a Î [1, )x Î +¥ eay x= £ ( ) e 0x af x x¢ = - ³ ( )f x [1, )x Î +¥ min( ) (1) 0f x f= = (e, )a Î +¥ 0 [1, )x Î +¥ ( ) e 0x af x x¢ = - = ( )f x 0 0[1, )x xÎ 0( )x +¥ 0( ) (1) 0f x f< = [1, )x Î +¥ ( ) 0f x ³ a ( ,e]-¥ ( ) e ln exf x a x= - - (1) e ln e 0xf a x= - - = ( ) e ln e 0xf x a x= - - ³ [1, )+¥ (1) 0f ′ ≥ ( ) ex af x x ′ = − (1) e 0f a′ = − ≥ ea ≤ 0a ≤ ( ) e 0x af x x ′ = − > ( )f x [1, )+¥ ( ) (1) 0f x f³ = ②当 时，在 时，有 ，知 ， 而在 时， ，知 ， 所以 在 上单调递增，即 （合题意） 综上所述， 的取值范围是 . 22. 【解析】（Ⅰ）由参数方程 得普通方程 ， 所以极坐标方程 ，即 . （Ⅱ）直线 与曲线 的交点为 ，得 ， 又直线 与曲线 的交点为 ，得 且 ，所以 . 23. 【解析】（Ⅰ）当 时， ， 得 ； 得 ； 得 ， 所以 的解集为 . （Ⅱ）对于任意实数 ，不等式 成立，即 恒成立， 又因为 ， 所以原不等式恒成立只需 ， 当 时，无解；当 时， ，解得 ； 当 时， ，解得 . 所以实数 的取值范围是 . 0 ea< ≤ 1x ≥ 10 1x < ≤ e 0aa x − ≤ − ≤ − < 1x > e ex ≥ ( ) e 0x af x x ′ = − ≥ ( )f x [1, )+¥ ( ) (1) 0f x f³ = a ( ,e]-¥ 2cos 2sin 2 x y θ θ =  = + 2 2( 2) 4x y+ − = 2 2 2 2cos sin 4 sin 0r q r q r q+ - = 4sinr q= ( )1 π: R6l q r= Î C ,O M | | 4sin 26M OM pr = = = ( )2 2π: R3l q r= Î C ,O N 2| | 4sin 2 33N ON pr = = = 2MON π∠ = 1 1| || | 2 2 3 2 32 2OMNS OM OND = = ´ ´ = 0a = ( ) | 2 | | 2 | | 2 | 3f x x x x+ - = + - ³ 0 2 2 3 x x x ì <ïïíï- + - ³ïî 1 3x £- 0 2 2 2 3 x x x ì £ £ïïíï + - ³ïî 1 2x£ £ 2 2 2 3 x x x ì >ïïíï + - ³ïî 2x > ( ) | 2 | 2f x x+ - ³ 1( , ] [1, )3-¥ - +¥ x | 2 1| ( ) 2x f x a+ - < 2| 2 1| | 2 3 | 2x x a a+ - + < 2 2 2| 2 1| | 2 3 | | 2 1 2 3 | | 3 1|x x a x x a a+ - + £ + - - = - 2| 3 1| 2a a- < 0a < 30 3a£ £ 21 3 2a a- < 1 3 3 3a< £ 3 3a > 23 1 2a a- < 3 13 a< < a 1( ,1)3