小学六年级奥数教案：平面几何综合(学生版)

小学六年级奥数教案：平面几何综合(学生版)

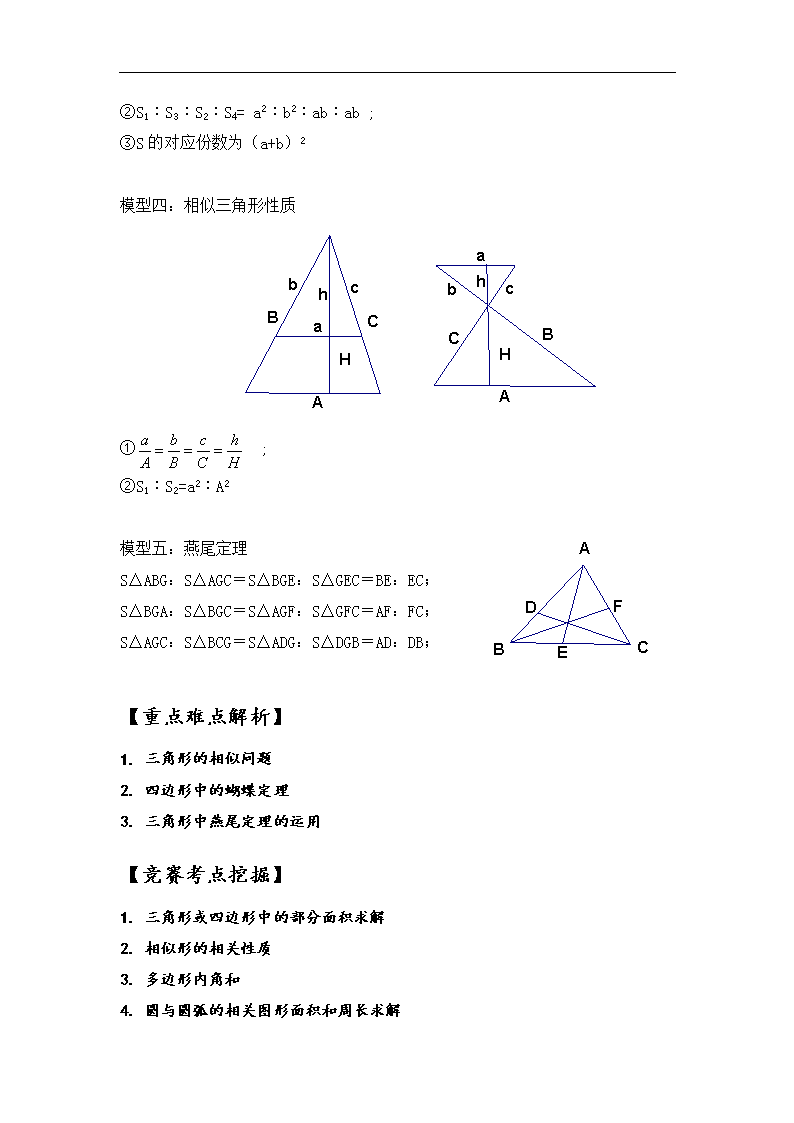
‎ 学科培优 数学 ‎ ‎“平面几何综合”‎ 学生姓名 授课日期 教师姓名 授课时长 知识定位 本讲复习以前所学过的有关平面几何方面的知识，包括直线型图形的五大模型以及圆与扇形方面的知识，旨在提高学生对该部分知识的综合运用能力。‎ 知识梳理 直线型图形五大模型 模型一：同一三角形中，相应面积与底的正比关系：‎ 即：两个三角形高相等，面积之比等于对应底边之比。‎ ‎ S1︰S2 =a︰b ；‎ 模型一的拓展： 等分点结论（“鸟头定理”）‎ 如图，三角形AED占三角形ABC面积的×= ‎ 模型二：任意四边形中的比例关系 （“蝴蝶定理”）‎ ① S1︰S2=S4︰S3 或者S1×S3=S2×S4 ‎ ② ‎②AO︰OC=（S1+S2）︰（S4+S3）‎ 模型三：梯形中比例关系（“梯形蝴蝶定理”）‎ ① S1︰S3=a2︰b2‎ ‎②S1︰S3︰S2︰S4= a2︰b2︰ab︰ab ; ‎ ‎③S的对应份数为（a+b）2‎ 模型四：相似三角形性质 ‎① ; ‎ ‎②S1︰S2=a2︰A2 ‎ 模型五：燕尾定理 S△ABG：S△AGC＝S△BGE：S△GEC＝BE：EC；‎ S△BGA：S△BGC＝S△AGF：S△GFC＝AF：FC；‎ S△AGC：S△BCG＝S△ADG：S△DGB＝AD：DB；‎ ‎【重点难点解析】‎ 1. 三角形的相似问题 2. 四边形中的蝴蝶定理 3. 三角形中燕尾定理的运用 ‎【竞赛考点挖掘】‎ 1. 三角形或四边形中的部分面积求解 2. 相似形的相关性质 3. 多边形内角和 4. 圆与圆弧的相关图形面积和周长求解 例题精讲 ‎【试题来源】‎ ‎【题目】如图，长方形ABCD中，阴影部分是直角三角形且面积为54，OD的长是16，OB的长是9.那么四边形OECD的面积是_____.‎ ‎【试题来源】‎ ‎【题目】如下左图.将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F.如果三角形ABC的面积等于l，那么三角形DEF的面积是_____.‎ ‎【试题来源】‎ ‎【题目】如图，三角形ABC的面积是1平方厘米，且BE=2EC，F是CD的中点．那么阴影部分的面积是( )平方厘米．‎ ‎【试题来源】‎ ‎【题目】如图，已知AE=AC，CD=BC，BF=AB，那么 ‎【试题来源】‎ ‎【题目】如图，BD是梯形ABCD的一条对角线，线段AE与梯形的一条腰DC平行，AE与BD相交于O点.已知三角形BOE的面积比三角形AOD的面积大4平方米，并且EC= BC.求梯形ABCD的面积.‎ ‎【试题来源】‎ ‎【题目】如图，平行四边形的花池边长分别为60米与30米．小明和小华同时从A点出发，沿着平行四边形的边由A→B→C→D→A…顺序走下去．小明每分钟走50米，小华每分钟走20米，出发5分钟后小明走到E点，小华走到F点．连结AE、AF，则四边形AECF的面积与平行四边形ABCD的面积的比是______．‎ ‎【试题来源】‎ ‎【题目】图中正方形周长是20厘米.那么图形的总面积是_____平方厘米.‎ 习题演练 ‎【试题来源】‎ ‎【题目】如图中，阴影部分的面积是5．7平方厘米，三角形ABC的面积是____‎ 平方厘米.（取3．14）‎ ‎【题目】图中，已知圆心是○，半径r=9厘米，∠1=∠2=，那么阴影部分的面积是_____平方厘米．(≈3.14) ‎ ‎【试题来源】‎ ‎【题目】图中阴影部分的面积是____平方厘米．(≈3.14)‎ ‎【试题来源】‎ ‎【题目】图中两个阴影部分面积的和是多少平方厘米?‎ ‎【试题来源】‎ ‎【题目】如右图，ABCD是正方形．E是BC边的中点，三角形ECF与三角 形ADF面积一样大，那么三角形AEF(阴影部分)的面积是正方形 ABCD面积的百分之____.（结果保留小数点后两位）‎ ‎【试题来源】‎ ‎【题目】图中ABCD是直角梯形，其中，AD=12厘米，AB=8厘米，BC=15厘米．且三角形ADE、四边形DEBF、三角形CDF的面积相等．那么三角形EBF的面积是______平方厘米．‎ ‎【试题来源】‎ ‎【题目】正方形ABCD的面积是160平方厘米，连接这个正方形4条边的中点，又得到一个正方形EFGH．像这样重复几次后得到下图，图中涂黑色部分的面积是____平方厘米．‎ ‎【试题来源】‎ ‎【题目】如图，三个一样大小的正方形放在一个长方形的盒内，A和B是两个正方形的重叠部分，C、D、E是空出的部分，每一部分都是矩形，它们的面积比是A：B：C：D：E=1：2：3：4：5，那么这个长方形的长与宽之比是________．‎ ‎【试题来源】‎ ‎【题目】已知四边形ABCD是直角梯形，上底AD=8厘米，下底BC=10厘米，直角腰CD=6厘米，E是AD的中点，F是BC上的点，BF=BC，G为DC上的点，三角形DEG的面积与三角形CFG的面积相等．那么，三角形ABG的面积是_____平方厘米．‎