- 2021-02-26 发布 |
- 37.5 KB |
- 12页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
五年级下册数学试题-几何综合(二)(含答案解析)全国通用
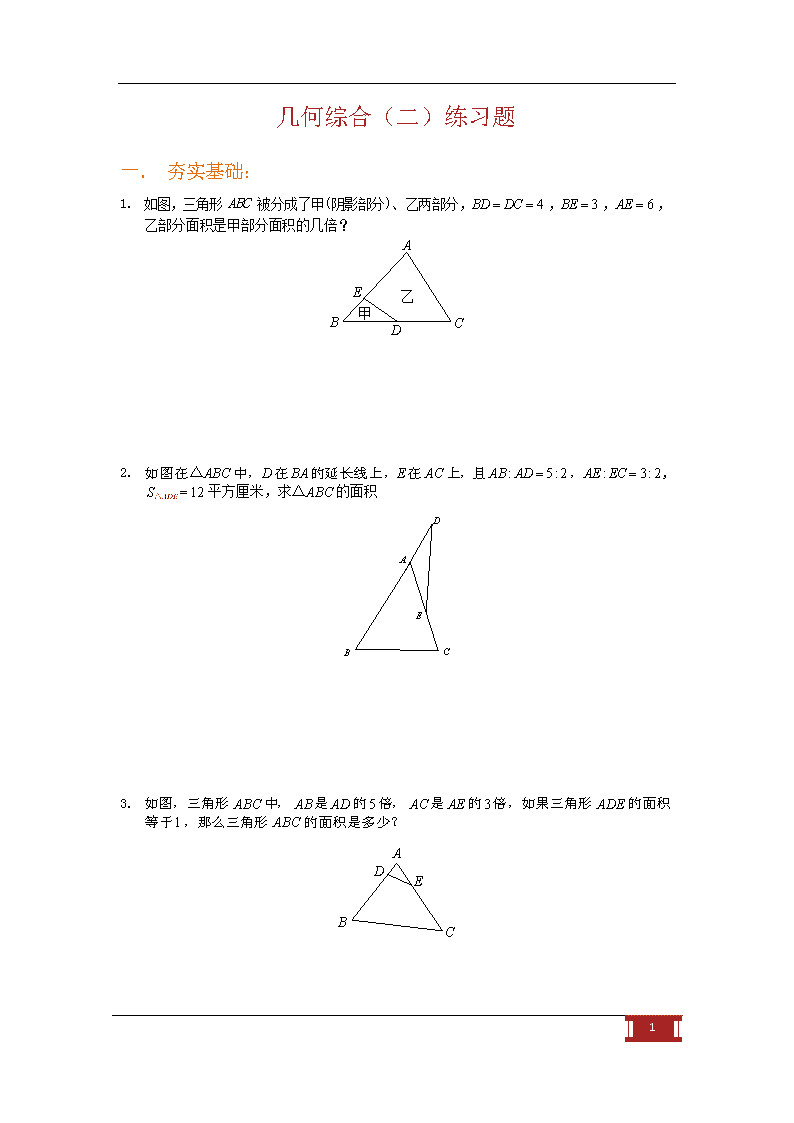
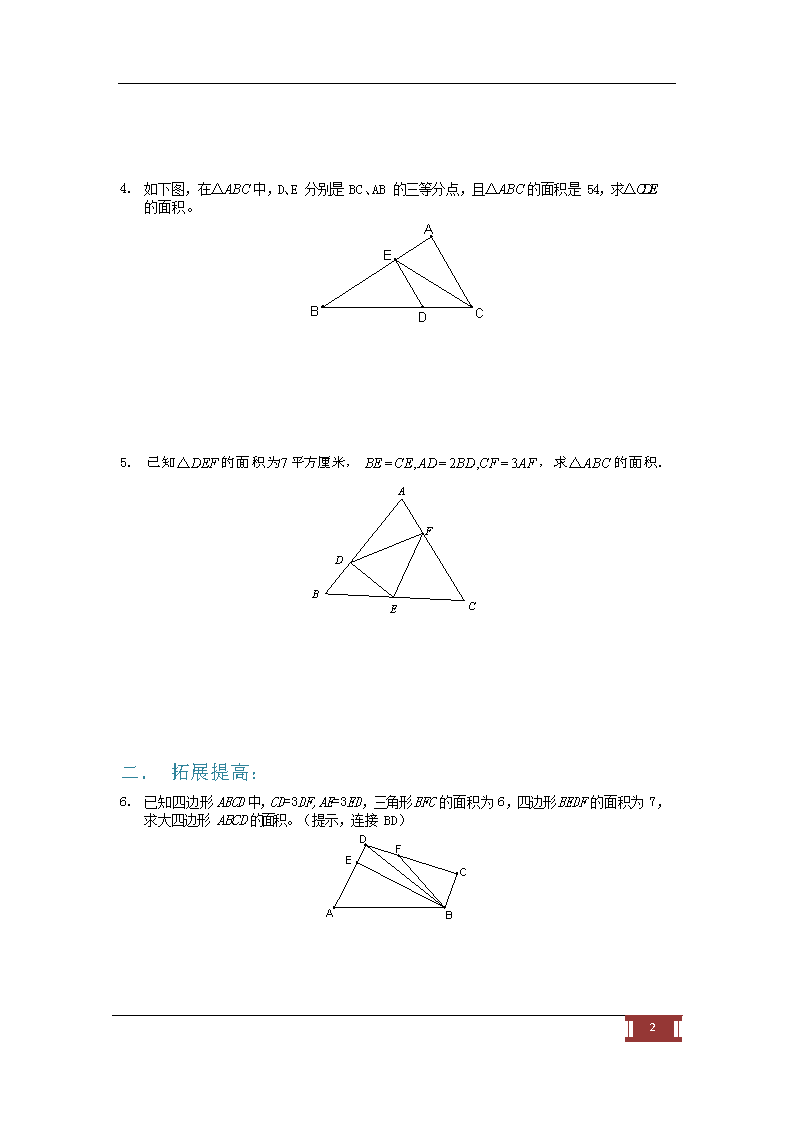
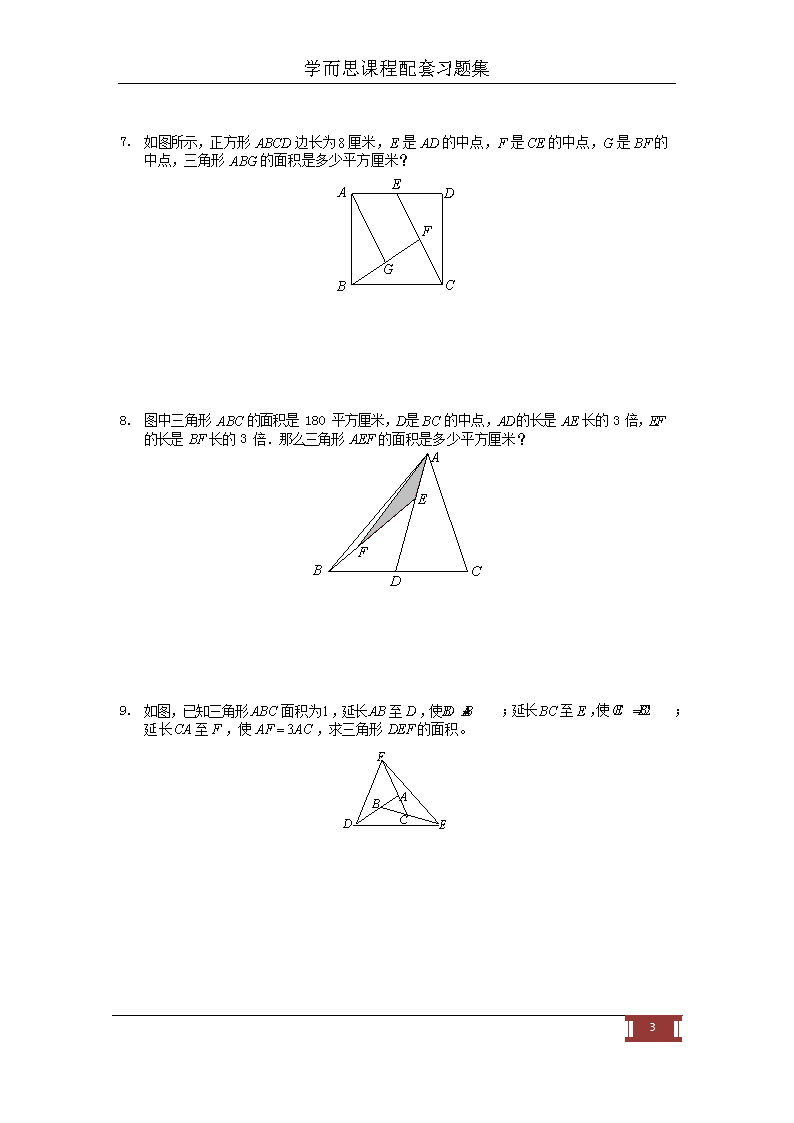
几何综合(二)练习题 一. 夯实基础: 如图,三角形 ABC 被分成了甲(阴影部分)、乙两部分,BD = DC = 4 ,BE = 3 ,AE = 6 , 乙部分面积是甲部分面积的几倍? A 1. E 乙 甲 B C D 如图在△ABC 中,D 在 BA 的延长线上,E 在 AC 上,且 AB : AD = 5 : 2 ,AE : EC = 3: 2 , S△ADE = 12 平方厘米,求△ABC 的面积 D 2. A E B C 3. 如图,三角形 ABC 中, AB 是 AD 的5 倍, AC 是 AE 的3 倍,如果三角形 ADE 的面积等于1 ,那么三角形 ABC 的面积是多少? A D E B C 1 4. 如下图,在△ABC 中,D、E 分别是 BC、AB 的三等分点,且△ABC 的面积是 54,求△CDE 的面积。 A E B C D 已知△DEF 的面积为7 平方厘米, BE = CE, AD = 2BD,CF = 3AF ,求△ABC 的面积. A 5. F D B C E 二. 拓展提高: 6. 已知四边形 ABCD 中,CD=3DF,AE=3ED,三角形 BFC 的面积为 6,四边形 BEDF 的面积为 7,求大四边形 ABCD 的面积。(提示,连接 BD) D F E C A B 2 学而思课程配套习题集 7. 如图所示,正方形 ABCD 边长为8 厘米,E 是 AD 的中点,F 是CE 的中点,G 是 BF 的中点,三角形 ABG 的面积是多少平方厘米? E A D C B 图中三角形 ABC 的面积是 180 平方厘米,D 是 BC 的中点,AD 的长是 AE 长的 3 倍,EF 的长是 BF 长的 3 倍.那么三角形 AEF 的面积是多少平方厘米? A 8. E F B C D 如图,已知三角形 ABC 面积为1 ,延长 AB 至 D ,使 BD AB= 延长CA 至 F ,使 AF = 3AC ,求三角形 DEF 的面积。 F CE =BC2 9. ;延长 BC 至 E ,使 ; A B D C E 3 F G 三. 超常挑战 10. 在四边形 ABCD 中,其对角线 AC、DB 交于 E 点。且 AF=CE,DE=BG。已知四边形 ABCD 的面积为 1,求△EFG 的面积是多少。 D C E A B F G 11. 如图,已知三角形 ABC 面积为1 ,延长 AB 至 D ,使 BD AB= 延长CA 至 F ,使 AF = 3AC ,求三角形 DEF 的面积. ;延长 BC 至 E ,使CE =BC2 ; F A E C B D 12. 如图,平行四边形 ABCD , BE = AB , CF = 2CB , GD = 3DC , HA = 4AD ,平行四边形 ABCD 的面积是2 , 求平行四边形 ABCD 与四边形 EFGH 的面积比. H A B E G C D F 4 13. 如图,四边形 EFGH 的面积是66 平方米,EA = AB ,CB = BF ,DC = CG ,HD = DA , 求四边形 ABCD 的面积. H C G D B A F E 14. 如图,将四边形 ABCD 的四条边 AB 、CB 、CD 、 AD 分别延长两倍至点 E 、 F 、G 、 H ,若四边形 ABCD 的面积为 5,则四边形 EFGH 的面积是 . F E B A C D G H 5 四. 杯赛演练: 15. (迎春杯决赛试题) 如图,长方形 ABCD 的面积是 1,M 是 AD 边的中点,N 在 AB 边上,且 AN = 1 BN .那 2 么,阴影部分的面积等于 . A M D N B C 图1 16. (四中考题) 如图, AD = DB , AE = EF = FC ,已知阴影部分面积为 5 平方厘米, DABC 的面积是平方厘米. B D A C E F 17. (“迎春杯”试题) 如图,三角形 ABC 的面积为 3 平方厘米,其中 AB : BE = 2 : 5 , BC : CD = 3: 2 ,三角形 BDE 的面积是多少? B E A C D 6 18. (“数学解题能力展示”试题)三角形 ABC 被线段 DE 分成三角形 BDE 和四边形 ACDE 两部分,问:三角形 BDE 的面积是四边形 ACDE 面积的几分之几? A 6 E 2 B D 3 4 C 7 答案: 1. 连接 AD . ∵ BE = 3 , AE = 6 ∴ AB = 3BE , S ABD = 3S BDE 又∵ BD = DC = 4 , ∴ S△ABC = 2S△ABD ,∴ S△ABC = 6S△BDE , S乙 = 5S甲 . A E 乙 B 甲 C D 连接 BE , S△ADE : S△ABE = AD : AB = 2 : 5 = (2 ´ 3) : (5´ 3) S△ABE : S△ABC = AE : AC = 3: (3 + 2) = (3´ 5) :[(3 + 2) ´ 5], 所以 S△ADE : S△ABC = (3´ 2) :[5´ (3 + 2)] = 6 : 25 ,设 S△ADE = 6 份,则 S△ABC 2. = 25 份, S△ADE = 12 平方厘米,所以1 份是2 平方厘米, 25 份就是50 平方厘米, △ABC 的面积是 50 平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 D A E B C 连接 BE .∵ AE = 1 EC 3 ∴ S = 1 S 3. . DABE DABC 3 又∵ AD = 1 AB ∴ S = 1 S 1 = S = 15S = 15 . ,∴ S △ADE △ABE △ABC △ABC △ADE 5 5 15 或者直接用共角定理即可 A D E B C 8 S = 2 S , S = 1 S Þ S = 2 ´ 1 S = 12 4. △BCE △ABC △CDE △BCE △CDE △ABC 3 3 3 3 S△BDE : S△ABC = (BD ´ BE) : (BA´ BC) = (1´1) : (2 ´ 3) =1: 6 S△CEF : S△ABC = (CE ´ CF) : (CB ´ CA) = (1´ 3) : (2 ´ 4) = 3: 8 S△ADF : S△ABC = (AD ´ AF) : (AB ´ AC) = (2 ´1) : (3´ 4) =1: 6 5. , = 24 份,则 S△BDE = 4 份, S△ADF = 4 份, S△CEF = 9 份, S△DEF = 24 - 4 - 4 - 9 = 7 设 S△ABC 份,恰好是7 平方厘米,所以 S△ABC = 24 平方厘米 6. 连接 BD,则 SDBDF = DF = 1 , S = 6 Þ S = 3ü ï Þ S DCBF DBDF S CF 2 = 4 ý DCBF DBDE ï S = 7 þ BEDF SDBDE = DE = 1 Þ S = 3S = 12 DABE DBDE S AE 3 DABE SABCD = 6 + 7 + 12 = 25 7. 连接 AF . 因为 S = S = 1 ´ 82 = 16 ,因此 S = 32 ,根据”当两个三角形有一个角相等或 △BCF △CDE ABFE 4 互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比” S = 8 ,所以 AEF S = 24 ,所以 S ABG = 12 平方厘米. ABF E A D C B △ABD , △ABC 等高,所以面积的比为底的比,有 S△ ABD = BD = 1 , BC 2 8. S△ ABC 所以 S = 1 ´ S = 1 ´180 = 90 (平方厘米).同理有 S AE ´ S = 1 ´ 90 = 30 = △ ABD ABC △ABE △ABD 2 2 AD 3 (平方厘米), S = FE ´ S = 3 ´30 = 22.5 (平方厘米).即三角形 AEF 的面积是 4 △AFE △ ABE BE 22.5 平方厘米 9 F G 9. 多次运用共角定理进行求解 AD ´ AF SDADF = 2 ´ 3 = 6 = AB ´ AC 1 1 SDABC SDBDE = BD ´ BE = 1 ´ 3 = 3 AB ´ AC 1 1 SDABC SDCEF = CE ´ CF = 2 ´ 4 = 8 AB ´ AC 1 1 SDABC SDDEF = 6 + 3 + 8 + 1 = 18 Þ S = 18S = 18 DDEF DABC S DABC AE ´ BE , SDADE = DE ´ AE , SDABE = 10. EF ´ BG EF ´ BG SDEFG SDBCE SDEFG BE ´ CE , SDCDE = DE ´ CE , = EF ´ BG EF ´ BG SDEFG SDEFG SABCD = AE ´ BE + DE ´ AE + BE ´ CE + DE ´ CE = (AE + CE) ´ (BE + DE) = AC ´ BD EF ´ BG EF ´ BG EF ´ BG SDEFG AF = CE Þ EF = AC; BG = DE Þ EG = BD SABCD = 1 Þ S = S = 1 DEFG ABCD S DEFG 11. 用共角定理∵在△ABC 和△CFE 中, ÐACB 与ÐFCE 互补, = AC × BC = 1´1 ∴ S△ ABC = 1 . FC × CE 4 ´ 2 8 S△FCE 又 S△ABC = 1,所以 S△FCE = 8 . 同理可得 S△ADF = 6 , S△BDE = 3 . = S△ABC + S△FCE + S△ADF + S△BDE = 1+ 8 + 6 + 3 = 18 . 所以 S△DEF F A E C B D 10 12. 连接 AC 、 BD .根据共角定理 ∵在△ABC 和△BFE 中, ÐABC 与ÐFBE 互补, = AB × BC = 1´1 = 1 . ∴ S△ ABC BE × BF 1´ 3 3 = 1,所以 S△FBE = 3 . S△FBE 又 S△ABC 同理可得 S△GCF = 8 , S△DHG = 15 , S△AEH = 8 . = S△AEH + S△CFG + S△DHG + S△BEF + SABCD = 8 + 8 +15+3+2 = 36 . 所以 SEFGH 所以 SABCD 2 1 = = . 36 18 SEFGH H A B E G C D F 13. 连接 BD .由共角定理得 S△BCD : S△CGF = (CD ´ CB) : (CG ´ CF) =1: 2 ,即 S△CGF 同理 S△ABD : S△AHE = 1: 2 ,即 S△AHE = 2S△ABD 所以 S△AHE + S△CGF = 2(S△CBD + S△ADB ) = 2S四边形ABCD = 2S△CDB 连接 AC ,同理可以得到 S△DHG + S△BEF = 2S四边形ABCD S四边形EFGH = S△AHE + S△CGF + S△HDG + S△BEF + S四边形ABCD = 5S四边形ABCD 所以 S四边形ABCD = 66 ¸ 5 = 13.2 平方米 H C G D A B F E 14. 连接 AC 、 BD . 由于 BE = 2AB , BF = 2BC ,于是 SDBEF = 4SDABC ,同理 SDHDG = 4SDADC . 于是 SDBEF + SDHDG = 4SDABC + 4SDADC = 4SABCD . 再由于 AE = 3AB , AH = 3AD ,于是 SDAEH = 9SDABD ,同理 SDCFG = 9SDCBD . 于是 SDAEH + SDCFG = 9SDABD + 9SDCBD = 9SABCD . 那么 SEFGH = SDBEF + SDHDG + SDAEH + SDCFG - SABCD = 4SABCD + 9SABCD - SABCD = 12SABCD = 60 . F E B A C D G H 11 设 AD = 2a , AB = 3b ,则 SABCD = 2a × 3b = 6ab = 1 15. . = 1 ab = 1 又因为 AM = a , AN = b ,则 S . △AMN 2 12 S =S - S = 1 - = 1 5 阴影 DABD DAMN 2 12 12 . S△ADE = S△DEF 16. S△ADE : S△ABC = (AE ´ AD) : (AC ´ AB) = (1´1) : (2 ´ 3) =1: 6 = 5´ 6 = 30 (平方厘米) 所以 S△ABC 17. 由于ÐABC + ÐDBE = 180° ,所以可以用共角定理,设 AB = 2 份, BC = 3份,则 BE = 5 份, BD = 3 + 2 = 5 份,由共角定理 S△ABC : S△BDE = (AB ´ BC) : (BE ´ BD) = (2 ´ 3) : (5´ 5) = 6 : 25 ,设 S△ABC = 6 份,恰好是3 平方厘米,所以1 份是0.5 平方厘米,25 份就是25´ 0.5 =12.5平方厘米,三角形 BDE 的面积是12.5 平方厘米 S△BDE 3 2 3 S△BDE 3 3 : S = = ´ = , = = . 18. 根据鸟头模型有 S △BDE △ABC 3 + 4 2 + 6 28 S 28 - 3 25 S △ABC 四边形ACDE 12查看更多