北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 2 第2课时矩形的判定

北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 2 第2课时矩形的判定

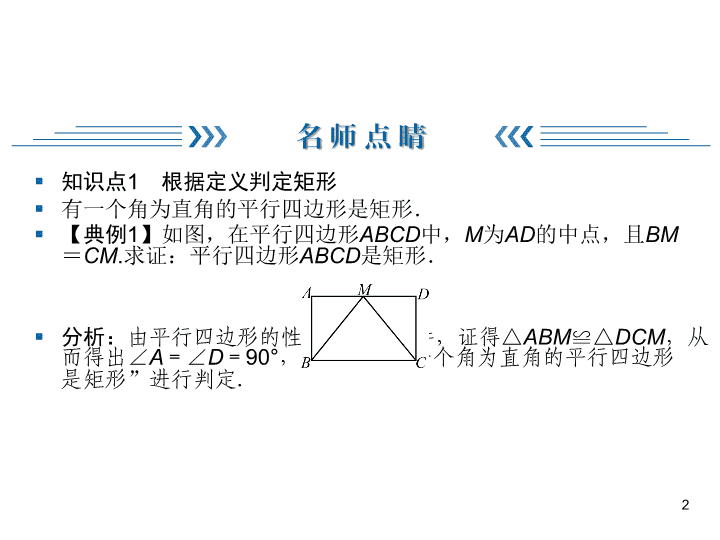
第一章　特殊平行四边形 2　矩形的性质与判定 第二课时　矩形的判定 § 知识点1　根据定义判定矩形 § 有一个角为直角的平行四边形是矩形． § 【典例1】如图，在平行四边形ABCD中，M为AD的中点，且BM ＝CM.求证：平行四边形ABCD是矩形． § 分析：由平行四边形的性质及已知条件，证得△ABM≌△DCM， 从而得出∠A＝∠D＝90°，再根据“有一个角为直角的平行四 边形是矩形”进行判定． 2 § 证明：∵四边形ABCD是平行四边形， § ∴AB＝CD，AB∥CD. § ∵M为AD的中点， § ∴AM＝DM. § 又∵BM＝CM， § ∴△ABM≌△DCM， § ∴∠A＝∠D. § ∵AB∥CD， § ∴∠A＋∠D＝180°， § ∴∠A＝∠D＝90°， § ∴平行四边形ABCD是矩形． 3 § 知识点2　矩形的判定定理 § 判定定理1：对角线相等的平行四边形是矩 形． § 由上面的定理可知：对角线相等且互相平分 的四边形是矩形．可以理解为：由“对角线 互相平分”可得此四边形为平行四边形，再 加上“对角线相等”，则为矩形． § 判定定理2：有三个角是直角的四边形是矩 形． 4 § 【典例2】如图，在矩形ABCD中，对角线 AC与BD相交于点O，点M、P、N、Q分别在 AO、BO、CO、DO上，且AM＝BP＝CN＝ DQ.求证：四边形MPNQ是矩形． § 分析：要证明四边形MPNQ是矩形，应先证 明它是平行四边形，再证其对角线相等． 5 § 证明：∵四边形ABCD是矩形， § ∴OA＝OB＝OC＝OD. § ∵AM＝BP＝CN＝DQ， § ∴OM＝OP＝ON＝OQ， § ∴四边形MPNQ是平行四边形． § 又∵OM＋ON＝OQ＋OP， § ∴MN＝PQ， § ∴四边形MPNQ是矩形． 6 § 1．两条平行线被第三条直线所截，两组内错角的平分线相交所成的四 边形是 § (　　) § A．任意四边形 B．平行四边形 § C．矩形 D．以上都不对 7 C 　 2．如图，四边形ABCD为平行四边形，延长AD到点E，使DE＝AD，连接 EB、EC、DB，添加一个条件，不能使四边形DBCE成为矩形的是(　　) A．AB＝BE B．BE⊥DC C．∠ADB＝90° D．CE⊥DE B 　 8 A 　 A 　 § 5．木工做一个长方形桌面，量得桌面的长为 45 cm，宽为28 cm，对角线为 53 cm，这 个桌面__________.(填“合格”或“不合 格”) § 6．如图，在平行四边形ABCD中，对角线 AC、BD相交于点O，且OA＝OB，∠OAD ＝65°，则∠ODC＝___________. 9 合格　 25°　 § 7．在矩形ABCD中，M为AD边的中点，P为BC上一点， PE⊥MC，PF⊥MB，当AB、BC满足条件______________时， 四边形PEMF为矩形． § 8．平行四边形ABCD的对角线相交于点O，分别添加下列条件： ①∠ABC＝90°；②AC⊥BD；③AB＝BC；④AC平分∠BAD； ⑤AO＝DO.使得四边形ABCD是矩形的条件有__________，是 菱形的条件有___________.(填序号) 10 ①⑤　 ②③④　 § 9．【2018·辽宁沈阳中考】如图，在菱形 ABCD中，对角线AC与BD交于点O.过点C作 BD的平行线，过点D作AC的平行线，两直线 相交于点E. § (1)求证：四边形OCED是矩形； § (2)若CE＝1，DE＝2，求菱形ABCD的面 积． 11 § 10．如图，△ABC中，D是AB上的一点，连接CD，DE平分∠BDC交 BC于点E，DF平分∠ADC交AC于点F，如果AD＝BD＝CD，求证：四 边形CEDF是矩形． 12 § 11．如图，将□ABCD的边AB延 长到点E，使BE＝AB，连接DE， 交边BC于点F. § (1)求证：△BEF≌ △CDF； § (2)连接BD、CE，若∠BFD＝ 2∠A，求证：四边形BECD是矩 形． 13 14