- 2021-02-26 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题复习练习:垂径定理及其应用
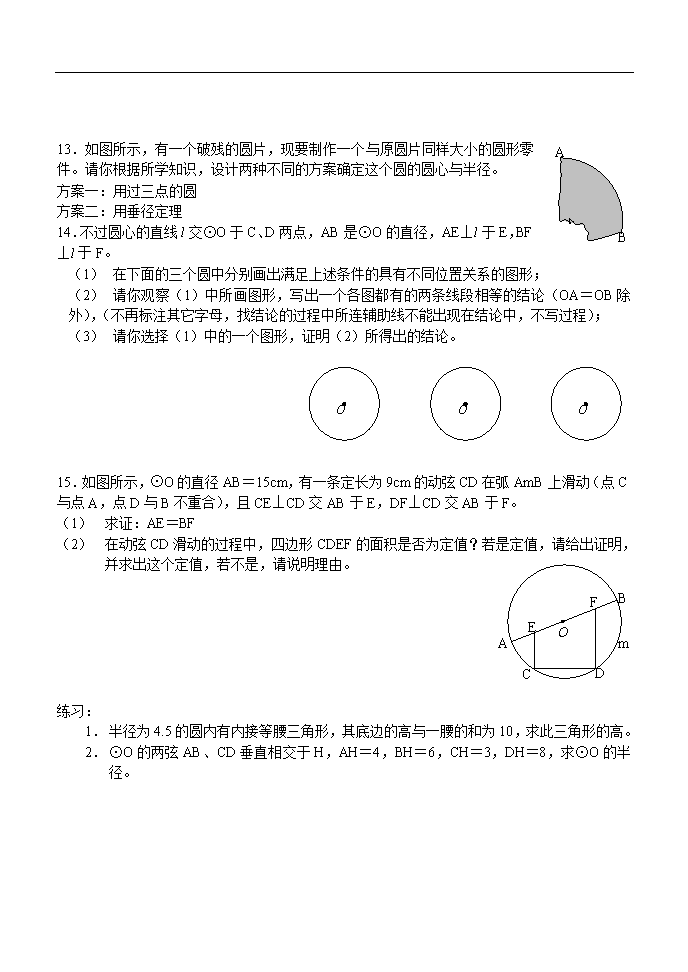
垂径定理及其应用 一.垂径定理的应用 口决: 垂径定理不一般; 题设结论二推三; 定理推论也重要, 总结起来共十条; 求半径,连半径, 弦的计算与证明; 巧作垂线过圆心,构造直角三角形。 1. 半径、弦心距、弦长、弓形高之间的计算:求半径、求弦心距、求弦长、求弓形高、求角、求平行弦的之间的距离 2. 证明线段相等、角相等、弧相等 3. 解决实际问题 二.垂径定理的推论的应用 1. 求半径、求弦心距、求弦长、求弓形高、求角 2. 等分弧(作图) 3. 确定圆心与半径(作图) 4. 解决实际问题 O A B D C 思想方法:分类讨论、数形结合 1. 已知:AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为_______。 2. 在⊙O中,P为其内一点,过点P的最长的弦为8cm,最短的弦长为4cm,则OP=_____。 3. 已知圆内接△ABC中,AB=AC,圆心O到BC的距离为3cm,半径r=7cm,则腰长AB为_________。 4. 已知圆的半径为5cm,一弦长为8cm,则该弦的中点到弦所对的弧的中点的距离为_______。 5. ⊙O的半径OA=1,弦AB、AC的长分别是,则∠BAC的度数为______。 6. 已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为_____。 O A B D C 7. 在半径为5cm的圆内有两条互相平行的弦,一条弦长为8cm,另一条弦长为6cm,则这两条弦之间的距离为______。 8. 如图,在⊙O中,OA是半径,弦AB=cm,D是弧AB的中点,OD交AB于点C,若∠OAB=300,则⊙O的半径____cm。 O A B C D 9. 在⊙O中,半径OA=10cm,AB是弦,C是AB弦的中点,且OC:AC=3:4,则AB=_____。 10.已知以O为圆心两个同心圆中,大圆的弦AB交小圆于C、D两点。求证:AC=BD O A B C D H 11.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,AB=10cm,CD=6cm,则AC的长为_____。 12.如图,在⊙O中,AB是直径,AB⊥CD,垂足为H,连结AC、AD、BC、BD,指出图中相等的锐角、相等的直角、相等的劣弧、相等的线段;相似的直角三角形。 A B 13.如图所示,有一个破残的圆片,现要制作一个与原圆片同样大小的圆形零件。请你根据所学知识,设计两种不同的方案确定这个圆的圆心与半径。 方案一:用过三点的圆 方案二:用垂径定理 14.不过圆心的直线l交⊙O于C、D两点,AB是⊙O的直径,AE⊥l于E,BF⊥l于F。 (1) 在下面的三个圆中分别画出满足上述条件的具有不同位置关系的图形; (2) 请你观察(1)中所画图形,写出一个各图都有的两条线段相等的结论(OA=OB除外),(不再标注其它字母,找结论的过程中所连辅助线不能出现在结论中,不写过程); (3) 请你选择(1)中的一个图形,证明(2)所得出的结论。 O O O 15.如图所示,⊙O的直径AB=15cm,有一条定长为9cm的动弦CD在弧AmB上滑动(点C与点A,点D与B不重合),且CE⊥CD交AB于E,DF⊥CD交AB于F。 (1) 求证:AE=BF O A B C D E F m (2) 在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明,并求出这个定值,若不是,请说明理由。 练习: 1. 半径为4.5的圆内有内接等腰三角形,其底边的高与一腰的和为10,求此三角形的高。 2. ⊙O的两弦AB、CD垂直相交于H,AH=4,BH=6,CH=3,DH=8,求⊙O的半径。查看更多