2020八年级数学下册一元一次不等式与一次函数

2020八年级数学下册一元一次不等式与一次函数

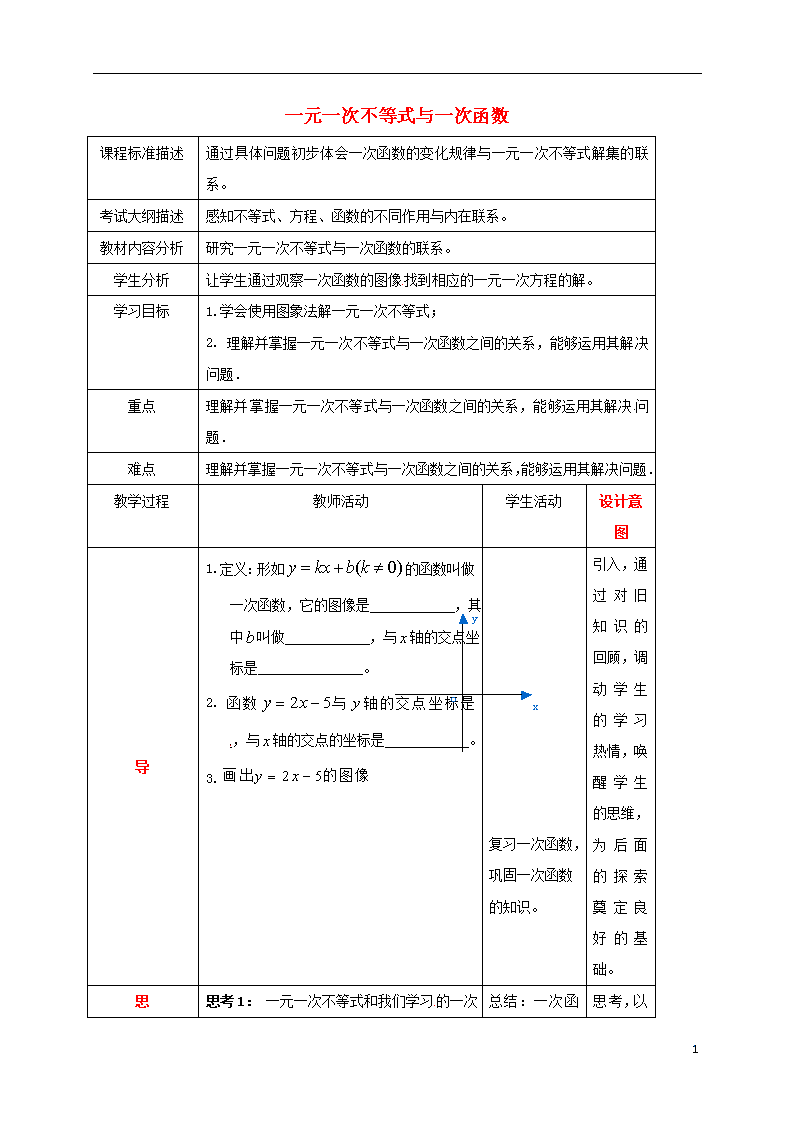
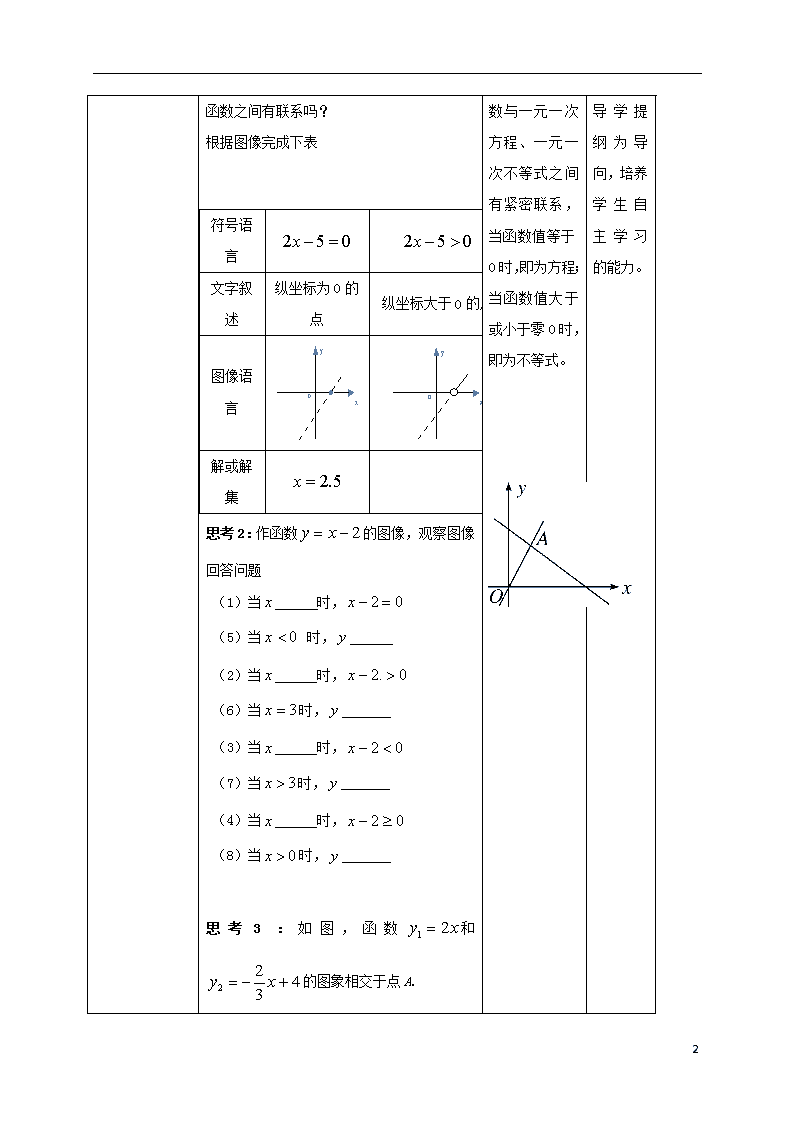
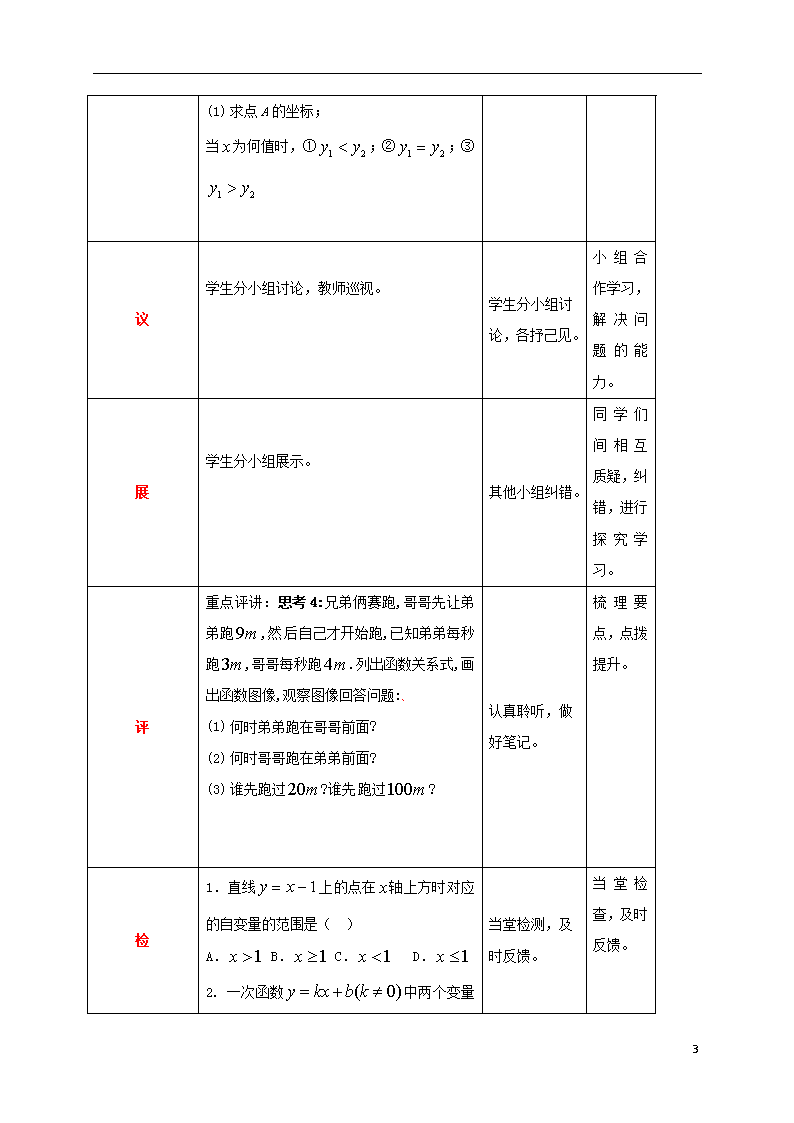
一元一次不等式与一次函数 课程标准描述 通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。‎ 考试大纲描述 感知不等式、方程、函数的不同作用与内在联系。‎ 教材内容分析 研究一元一次不等式与一次函数的联系。‎ 学生分析 让学生通过观察一次函数的图像找到相应的一元一次方程的解。‎ 学习目标 ‎1.学会使用图象法解一元一次不等式；‎ ‎2. 理解并掌握一元一次不等式与一次函数之间的关系，能够运用其解决问题．‎ 重点 理解并掌握一元一次不等式与一次函数之间的关系，能够运用其解决问题．‎ 难点 理解并掌握一元一次不等式与一次函数之间的关系，能够运用其解决问题．‎ 教学过程 教师活动 学生活动 设计意图 导 1. 定义：形如的函数叫做一次函数，它的图像是 ，其中叫做 ，与轴的交点坐标是 。‎ 2. ‎ 函数与轴的交点坐标是 ，与轴的交点的坐标是 。‎ 3. 复习一次函数，巩固一次函数的知识。‎ 引入，通过对旧知识的回顾，调动学生的学习热情，唤醒学生的思维，为后面的探索奠定良好的基础。‎ 思 思考1： 一元一次不等式和我们学习 总结：‎ 思 4‎ 的一次函数之间有联系吗？‎ 根据图像完成下表 符号语言 文字叙述 纵坐标为0的点 纵坐标大于0的点 图像语言 解或解集 思考2：作函数的图像，观察图像回答问题 ‎ （1）当 时， ‎ ‎（5）当 时， ‎ ‎ （2）当 时， ‎ ‎（6）当时， ‎ ‎ （3）当 时， ‎ ‎（7）当时， ‎ ‎ （4）当 时， ‎ ‎（8）当时， ‎ 思考3：如图，函数和的图象相交于点A.‎ 一次函数与一元一次方程、一元一次不等式之间有紧密联系，当函数值等于0时，即为方程；当函数值大于或小于零0时，即为不等式。‎ 考，以导学提纲为导向，培养学生自主学习的能力。‎ 4‎ (1) 求点A的坐标；‎ 当为何值时，①；②；③‎ 议 学生分小组讨论，教师巡视。‎ 学生分小组讨论，各抒己见。‎ 小组合作学习，解决问题的能力。‎ 展 学生分小组展示。‎ 其他小组纠错。‎ 同学们间相互质疑，纠错，进行探究学习。‎ 评 重点评讲：思考4:兄弟俩赛跑,哥哥先让弟弟跑,然后自己才开始跑,已知弟弟每秒跑,哥哥每秒跑.列出函数关系式,画出函数图像,观察图像回答问题:‎ (1) 何时弟弟跑在哥哥前面?‎ (2) 何时哥哥跑在弟弟前面?‎ (3) 谁先跑过?谁先跑过?‎ 认真聆听，做好笔记。‎ 梳理要点，点拨提升。‎ 检 ‎1．直线上的点在轴上方时对应的自变量的范围是（ ）‎ A． B． C． D．‎ ‎2. 一次函数中两个变量 当堂检测，及时反馈。‎ 当堂检查，及时反馈。‎ 4‎ 的部分对应值如下表所示：‎ x ‎…‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎8‎ ‎5‎ ‎2‎ ‎－1‎ ‎－4‎ ‎…‎ 那么关于的不等式的解集是___ _____．‎ ‎3. 已知直线与相交于点（2，0），则不等式的解集是________．‎ 教学反思 通过数形结合，对不等式及函数联系认识的理解。‎ 4‎