2020年中考数学总复习 第15讲 等腰、等边、直角三角形 新版 新人教版

2020年中考数学总复习 第15讲 等腰、等边、直角三角形 新版 新人教版

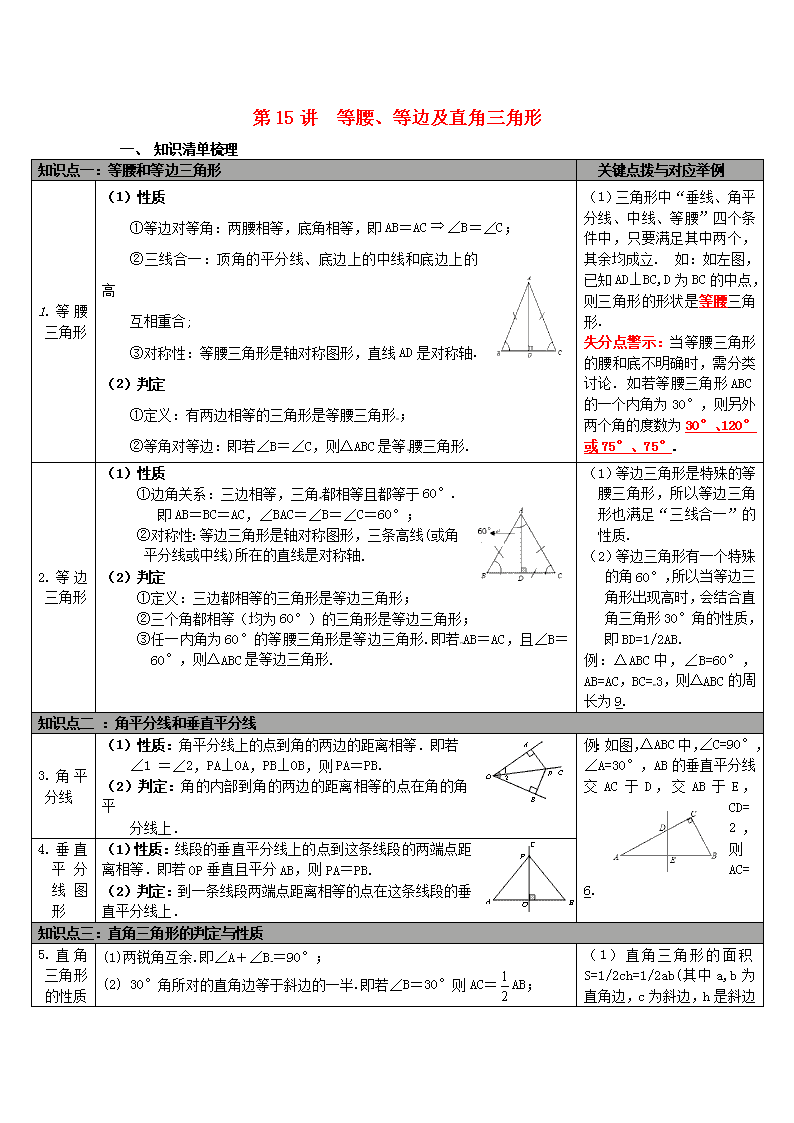
第15讲 等腰、等边及直角三角形 一、 知识清单梳理 知识点一：等腰和等边三角形 ‎ ‎ 关键点拨与对应举例 ‎1.等腰三角形 ‎（1）性质 ‎①等边对等角：两腰相等，底角相等，即AB＝AC∠B＝∠C；‎ ‎②三线合一：顶角的平分线、底边上的中线和底边上的高 互相重合; ‎ ‎③对称性：等腰三角形是轴对称图形，直线AD是对称轴.‎ ‎（2）判定 ‎①定义：有两边相等的三角形是等腰三角形；‎ ‎②等角对等边：即若∠B＝∠C，则△ABC是等腰三角形. ‎ ‎（1）三角形中“垂线、角平分线、中线、等腰”四个条件中，只要满足其中两个，其余均成立. 如：如左图，已知AD⊥BC,D为BC的中点，则三角形的形状是等腰三角形.‎ 失分点警示：当等腰三角形的腰和底不明确时，需分类讨论. 如若等腰三角形ABC的一个内角为30°，则另外两个角的度数为30°、120°或75°、75°.‎ ‎2.等边三角形 ‎（1）性质 ‎①边角关系：三边相等，三角都相等且都等于60°.‎ 即AB＝BC＝AC，∠BAC＝∠B＝∠C＝60°；‎ ‎②对称性：等边三角形是轴对称图形，三条高线(或角平分线或中线)所在的直线是对称轴.‎ ‎（2）判定 ‎①定义：三边都相等的三角形是等边三角形； ‎ ‎②三个角都相等（均为60°）的三角形是等边三角形；‎ ‎③任一内角为60°的等腰三角形是等边三角形.即若AB＝AC，且∠B＝60°，则△ABC是等边三角形.‎ ‎（1）等边三角形是特殊的等腰三角形，所以等边三角形也满足“三线合一”的性质.‎ ‎（2）等边三角形有一个特殊的角60°，所以当等边三角形出现高时，会结合直角三角形30°角的性质，即BD=1/2AB.‎ 例：△ABC中，∠B=60°，AB=AC，BC=3，则△ABC的周长为9.‎ 知识点二 ：角平分线和垂直平分线 ‎3.角平分线 ‎（1）性质：角平分线上的点到角的两边的距离相等．即若 ‎∠1 ＝∠2，PA⊥OA，PB⊥OB，则PA＝PB.‎ ‎（2）判定：角的内部到角的两边的距离相等的点在角的角平 分线上．‎ 例：如图，△ABC中，∠C=90°，∠A=30°，AB的垂直平分线交AC于D，交AB于E，CD=2，则AC=6.‎ ‎4.垂直平分线图形 ‎（1）性质：线段的垂直平分线上的点到这条线段的两端点距离相等．即若OP垂直且平分AB，则PA＝PB.‎ ‎（2）判定：到一条线段两端点距离相等的点在这条线段的垂直平分线上． ‎ 知识点三：直角三角形的判定与性质 ‎5.直角三角形的性质 ‎(1)两锐角互余.即∠A＋∠B＝90°；‎ ‎(2) 30°角所对的直角边等于斜边的一半.即若∠B＝30°则AC＝AB；‎ ‎（1）直角三角形的面积S=1/2ch=1/2ab(其中a,b为直角边，c为斜边，h (3) 斜边上的中线长等于斜边长的一半．即若CD是中线，则CD＝AB.‎ (4) 勾股定理：两直角边a、b的平方和等于斜边c的平方．即 a2＋b2＝c2 .‎ 是斜边上的高)，可以利用这一公式借助面积这个中间量解决与高相关的求长度问题.‎ ‎（2）已知两边，利用勾股定理求长度，若斜边不明确，应分类讨论.‎ ‎（3）在折叠问题中，求长度，往往需要结合勾股定理来列方程解决.‎ ‎6.直角三角形的判定 ‎(1) 有一个角是直角的三角形是直角三角形.即若∠C＝90°，则△ABC是Rt△；‎ ‎(2) 如果三角形一条边的中线等于这条边的一半，那么这个三角形是直角三角形．即若AD＝BD＝CD，则△ABC是Rt△‎ ‎(3) 勾股定理的逆定理：若a2＋b2＝c2，则△ABC是Rt△.‎ 一、 典例试做：‎ 内参P56---5、6、7、17、20‎ P58---1、2、4、11、17‎ 三、课后反思：‎