- 2021-02-26 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
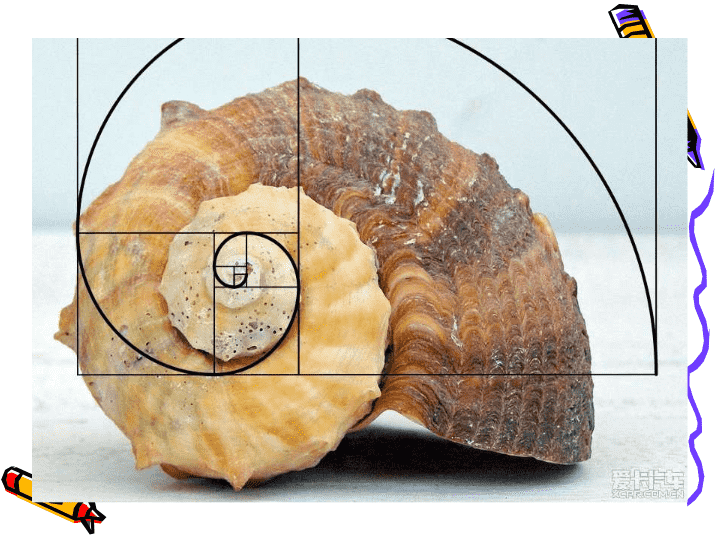
六年级上册数学课件-《黄金螺旋线》北京版 (共25张PPT)
黄金螺旋线 提示: 你可以把图中的几个扇形的半径一一列出来,再结合画图或拼摆来发现规律。 小组合作: 1 、你发现了什么规律? 2 、你是怎样发现这个规律的? 3 、根据发现的规律,把这串数继续写下去,至少写三个。 1 、 1 、 2 、 3 、 5 、 8 …… 从第三个扇形起,每个小扇形的半径都是它前面相邻两个扇形半径之和。 我们发现的规律是什么? 我们是怎样发现规律的? 1 、 1 、 2 、 3 、 5 、 8 、 13 、 21 、 通过我们发现的规律,把这串数继续写下去,多写出几个 34 、 55 、 89 144 、 233 、 377 、 610 、 987······ 这串数就是著名的“ 斐波那契数列 ”。 13 世纪初,欧洲最好的数学家是意大利的斐波拉契,他写了一本叫作 《 算盘书 》 的著作,是当时欧洲最好的数学书。书中有许多有趣的数学题,其中最有趣的是下面这个题目: 兔子繁殖问题 月份 1 2 3 4 5 6 7 8 9 10 11 12 兔子总对数 2 3 5 8 13 21 34 55 89 144 233 377 如果一对兔子每月能生 1 对小兔子,而每对小兔子在它出生后的第三个月里,又能开始生 1 对小兔子,假定在不发生死亡的情况下,由一对兔子开始,一年后能繁殖成多少对兔子? 可列表如下: 就是说,由一对兔子开始,满一年时一共可繁殖成 377 对小兔。 特别值得指出的是,数学家斐波那契没有满足于这个问题有了答案。他进一步对各个月的兔子对数进行了仔细观察,从中发现了一个十分有趣的规律,就是后面一个月份的兔子总对数,恰好等于前面两个月份兔子总对数的和,如果再把原来兔子的对数重复写一次,于是就得到了下面这样的一串数: 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377…… 后来人们为了纪念这位数学家,就把上面这样的一串数称作斐波那契数列,又称“兔子数列”,所以“黄金螺旋线”也称“斐波那契数列”,是根据斐波那契数列画出来的螺旋曲线,自然界当中存在许多斐波那契螺旋线的图案。人们根据“黄金螺旋线”也创造出了许多优美的作品。 计算机绘制的斐波纳契螺旋 考考你: 有一串数从第三个数开始,每个数都是它前两个数的和,已知这串数的第六个数是 6.5 ,第七个数是 10.5 ,那么这串第五个数是多少?第一个数是几? 这节课你有什么收获? 我们为什么学习数学? 数学是自然之源,唯有它能如此奇妙而精准的表达世界,一分一毫也不差。 数学能使我们在思考时将复杂的问题变得简单明了,更容易分析。 一群阿拉伯人逃难在外,到了一条满是沙砾的河边。半夜,一位智者梦见真主让他在第二天启程的时候捡尽量多的沙砾带走。虽然不明白是什么意思,但他们还是照办了 , 当然也有人嗤之以鼻。当走出很远之后,他们发现手中的石块变成了珠宝,但是那条神奇的河却再也找不到了。我们不可能确切的知道自己今天学的东西什么时候会用上,但如果要等将来,我们失去的将无法挽回。 数学是一种思考的学问、探索的学问。 从有趣的数学出发让我们开始喜欢数学吧!哪怕只是为了不让大脑停顿。 上帝忘了给我们翅膀,所以我们用数学飞翔! 下 课 啦 !查看更多