2020高中数学 课时分层作业4 演绎推理 新人教A版选修1-2
课时分层作业(四) 演绎推理
(建议用时:40分钟)
[基础达标练]
一、选择题
1.“所有金属都能导电,铁是金属,所以铁能导电”这种推理方法属于( )
A.演绎推理 B.类比推理
C.合情推理 D.归纳推理
A [大前提为所有金属都能导电,小前提是金属,结论为铁能导电,故选A.]
2.已知在△ABC中,∠A=30°,∠B=60°,求证:BC
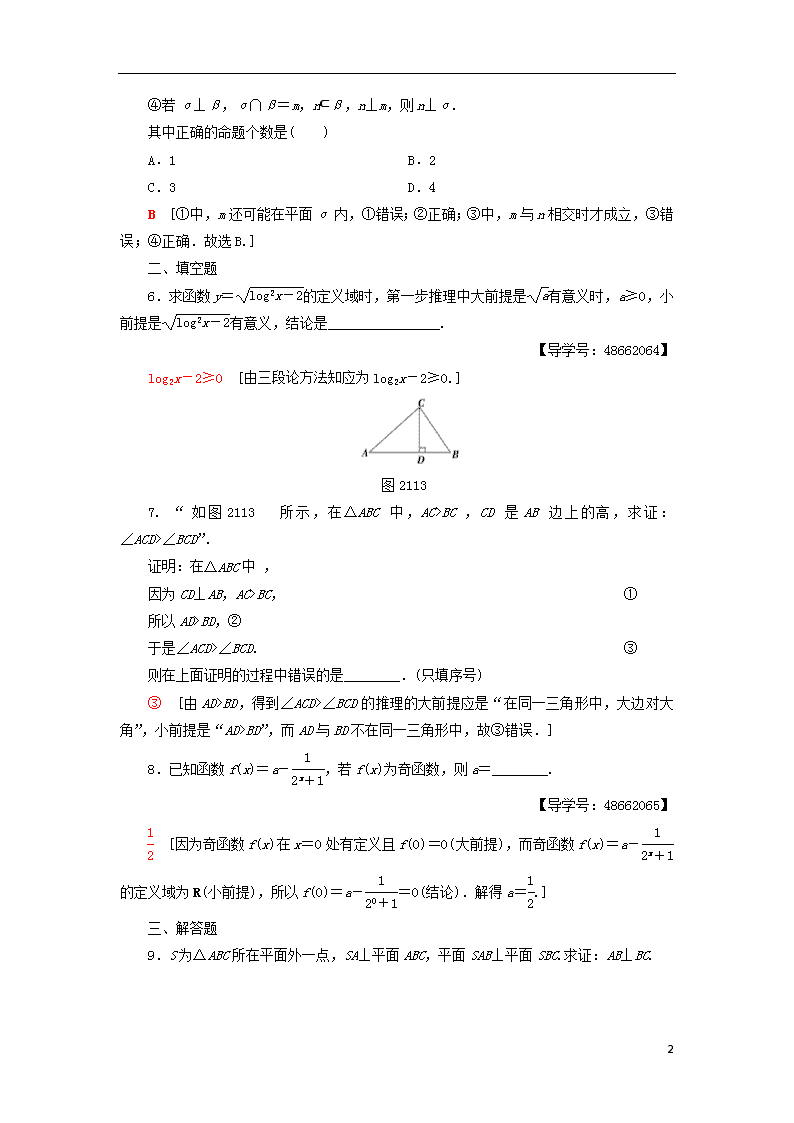
BC,CD是AB边上的高,求证:∠ACD>∠BCD”.
证明:在△ABC中 ,
因为CD⊥AB,AC>BC, ①
所以AD>BD,②
于是∠ACD>∠BCD. ③
则在上面证明的过程中错误的是________.(只填序号)
③ [由AD>BD,得到∠ACD>∠BCD的推理的大前提应是“在同一三角形中,大边对大角”,小前提是“AD>BD”,而AD与BD不在同一三角形中,故③错误.]
8.已知函数f(x)=a-,若f(x)为奇函数,则a=________.
【导学号:48662065】
[因为奇函数f(x)在x=0处有定义且f(0)=0(大前提),而奇函数f(x)=a-的定义域为R(小前提),所以f(0)=a-=0(结论).解得a=.]
三、解答题
9.S为△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC.求证:AB⊥BC.
5
[证明] 如图,作AE⊥SB于E.
∵平面SAB⊥平面SBC,平面SAB∩平面SBC=SB.AE⊂平面SAB.
∴AE⊥平面SBC,
又BC⊂平面SBC.
∴AE⊥BC.又∵SA⊥平面ABC,
∴SA⊥BC.
∵SA∩AE=A,SA⊂平面SAB,AE⊂平面SAB,
∴BC⊥平面SAB.
∵AB⊂平面SAB.∴AB⊥BC.
10.已知a,b,m均为正实数,b<a,用三段论形式证明<.
[证明] 因为不等式两边同乘以一个正数,不等号不改变方向,(大前提)
b<a,m>0,(小前提)
所以mb<ma.(结论)
因为不等式两边同加上一个数,不等号不改变方向,(大前提)
mb<ma,(小前提)
所以mb+ab<ma+ab,即b(a+m)<a(b+m).(结论)
因为不等式两边同除以一个正数,不等号不改变方向,(大前提)
b(a+m)<a(b+m),a(a+m)>0,(小前提)
所以<,即<.(结论)
[能力提升练]
1.“所有9的倍数(M)都是3的倍数(P),某奇数(S)是9的倍数(M),故某奇数(S)是3的倍数(P).”上述推理是( )
【导学号:48662066】
A.小前提错 B.结论错
C.正确的 D.大前提错
C [由三段论推理概念知推理正确.]
2.下面几种推理中是演绎推理的是( )
A.因为y=2x是指数函数,所以函数y=2x经过定点(0,1)
5
B.猜想数列,,,…的通项公式为an=(n∈N*)
C.由“平面内垂直于同一直线的两直线平行”类比推出“空间中垂直于同一平面的两平面平行”
D.由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2
A [A为演绎推理,这里省略了大前提,B为归纳推理,C,D为类比推理.]
3.以下推理中,错误的序号为________.
【导学号:48662067】
①∵ab=ac,∴b=c;
②∵a≥b,b>c,∴a>c;
③∵75不能被2整除,∴75是奇数;
④∵a∥b,b⊥平面α,∴a⊥α.
① [当a=0时,ab=ac,但b=c未必成立.]
4.已知f(1,1)=1,f(m,n)∈N*(m,n∈N*),且对任意m,n∈N*都有:
①f(m,n+1)=f(m,n)+2;②f(m+1,1)=2f(m,1)给出以下三个结论:
(1)f(1,5)=9;(2)f(5,1)=16;(3)f(5,6)=26.
其中正确结论为________.
(1)(2)(3) [由条件可知,
因为f(m,n+1)=f(m,n)+2,且f(1,1)=1,
所以f(1,5)=f(1,4)+2=f(1,3)+4=f(1,2)+6=f(1,1)+8=9.
又因为f(m+1,1)=2f(m,1),
所以f(5,1)=2f(4,1)=22f(3,1)=23f(2,1)=24f(1,1)=16,
所以f(5,6)=f(5,1)+10=16+10=26.
故(1)(2)(3)均正确.]
5.在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)证明:数列{an-n}是等比数列.
(2)求数列{an}的前n项和Sn.
(3)证明:不等式Sn+1≤4Sn,对任意n∈N*皆成立.
【导学号:48662068】
[解] (1)证明:因为an+1=4an-3n+1,
所以an+1-(n+1)=4(an-n),n∈N*.
又a1-1=1,所以数列{an-n}是首项为1,且公比为4的等比数列.
(2)由(1)可知an-n=4n-1,于是数列{an}的通项公式为an=4n-1+n.
5
所以数列{an}的前n项和Sn=+.
(3)证明:对任意的n∈N*, Sn+1-4Sn=+-4=-(3n2+n-4)≤0.
所以不等式Sn+1≤4Sn,对任意n∈N*皆成立.
5