- 2021-06-25 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
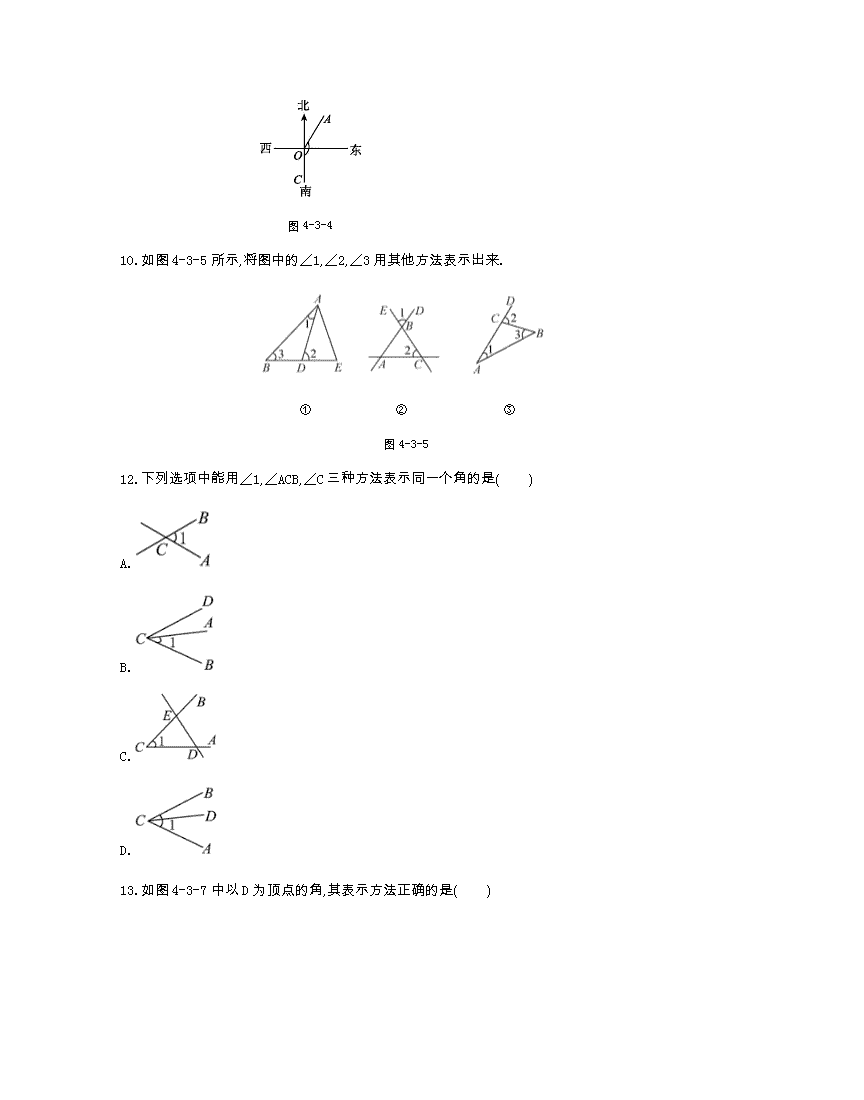
北师七年级数学上册 第四章二节 同步课时检测卷(附参考答案)
北师七上数学测试题第四章二节 1.角是由 条具有公共端点的 组成的图形,其中,公共端点叫做角的 ,两条 叫做角的边;角也可以看成是由 条射线绕着它的端点 而形成的图形.旋转开始时的射线叫做角的 ,旋转终止时的射线叫做角的 .一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做 .终边继续旋转,当它又和始边重合时,所成的角叫做 . 2.角的表示方法。 ①三个 英文字母; ②一个 英文字母; ③ 字母; ④ 数字. 如图4-3-1所示,该角可记作 、 、 ,也可用希腊字母记为∠α. 图4-3-1 3.度量角的工具是 . 4.角的单位度(°)、分(’)、秒(”),1°= ’,1’= ”. 5.如图4-3-2所示. (1)以B为顶点的角有几个?把它们表示出来; (2)指出以射线BA为边的角; (3)以D为顶点,射线DC为一边的角有几个?分别表示出来. 图4-3-2 6.下列说法正确的是( ) A.两条射线组成的图形叫做角 B.平角的两边构成一条直线 C.角的两边都可以任意延长 D.由射线OA,OB组成的角,可以记作∠AOB,也可以记作∠ABO 7.如图4-3-3所示,给出两种说法:(1)∠A也可以表示为∠BAC,(2)∠α也可以表示为∠BAC.其中,正确的说法( ) 图4-3-3 A.只有(1) B.只有(2) C.两个都正确 D.全都不正确 8.钟表上的时间为晚上8点,这时时针和分针之间的夹角(小于平角)的度数是( ) A.120° B.105° C.100° D.90° 9.如图4-3-4,∠AOC=150°,则射线OA的方向是 . 图4-3-4 10.如图4-3-5所示,将图中的∠1,∠2,∠3用其他方法表示出来. ① ② ③ 图4-3-5 12.下列选项中能用∠1,∠ACB,∠C三种方法表示同一个角的是( ) A. B. C. D. 13.如图4-3-7中以D为顶点的角,其表示方法正确的是( ) 图4-3-7 A.∠DAE B.∠ADE C.∠D D.∠AED 14.点A在点O的南偏东30°,点B在点O的北偏西70°,则OA,OB这两条射线构成的角等于( ) A.140° B.100° C.80° D.40° 16.(1)54.12°= ° ’ ”; (2)65°25’12”= °; (3)0.5°= ’= ”; (4)2160”= °= ’; (5)57.32°= ° ’ ”. 17.如图4-3-9所示,从一点O出发引射线OA,OB,OC,OD,请你数一数图中有多少个角,并把它们表示出来. 图4-3-9 18.王老师到市场去买菜,发现如果把10千克的菜放到秤上,指标盘上的指针转了180°.秤如图4-3-10所示,第二天王老师就给同学们出了两个问题。 图4-3-10 (1)如果把0.5千克的菜放在秤上,指针转过多少角度? (2)如果指针转了54°,这些菜有多少千克? 19.角的大小是指 的大小,只与开口大小有关,与边的长短无关. 20.从一个角的 处引出一条射线,把这个角分成两个 的角,这条 叫做这个角的平分线. 21.下面的式子中,能表示“OC是∠AOB的平分线”的等式是( ) A.2∠AOC=∠BOC B.∠AOC=∠AOB C.∠AOB=2∠BOC D.∠AOC=∠BOC 22.如图4-4-1所示,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( ) 图4-4-1 A.20° B.40° C.50° D.80° 23.图4-4-2中最大的角是 ,∠DOC,∠DOB,∠DOA的大小关系是 . 图4-4-2 24.如图4-4-3所示,∠AOB=∠COD,请判断∠AOC和∠BOD的大小关系,并说明理由. 图4-4-3 25.如图4-4-4所示,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.若∠AOC=120°,∠BOC=30°,求∠DOE. 图4-4-4 26.若∠A=20°18’,∠B=20°15’30”,∠C=20.25°,则( ) A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C>∠B D.∠C>∠A>∠B 27.如图4-4-5所示,∠AOB=∠COA-∠ =∠DOA-∠ . 图4-4-5 28.如图4-4-6所示,∠AOC=36°,OC平分∠AOB,则∠AOB= . 图4-4-6 29.根据图4-4-7中的图形,解答下列问题。 (1)比较∠AOB,∠AOC,∠AOD,∠AOE的大小,并指出其中的锐角、直角、钝角、平角; 图4-4-7 (2)写出∠AOB,∠AOC,∠BOC,∠AOE中各角之间的2个等量关系. 30.如图4-4-8所示,已知∠AOB=∠BOC,∠COD=∠AOD=3∠AOB,求∠AOB和∠COD的度数. 图4-4-8 31.如图4-4-9,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°. 图4-4-9 (1)求出∠BOD的度数; (2)请通过计算说明:OE是否平分∠BOC. 参考答案 1.两 射线 顶点 射线 一 旋转 始边 终边 平角 周角 2.①大写 ②大写 ③希腊 ④阿拉伯 ∠AOB ∠O、∠1 3.量角器 4.60 60 5.(1)解:以B为顶点的角有3个,分别为∠ABE,∠ABC,∠CBE. (2)解:∠ABE,∠ABC. (3)解:4个,∠CDB,∠EDC,开口DE方向的∠ADC,开口DB方向的∠ADC. 6.B 7.C 8.A 9.北偏东30° 10.解:图①中,∠1可表示为∠BAD,∠2可表示为∠ADE,∠3可表示为∠ABD或∠ABE或∠B.图②中,∠1可表示为∠EBD,∠2可表示为∠ACB或∠ACE.图③中,∠1可表示为∠A或∠CAB或∠DAB,∠2可表示为∠DCB,∠3可表示为∠B或∠ABC. 12.C 13.B 14.A 16.(1)54 7 12 (2)65.42 (3)30 1800 (4)0.6 36 (5)57 19 12 17.解:共6个角,它们是:∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD. 18.(1)解:(1)因为=18°,所以0.5×18°=9°. 所以0.5千克的菜放在秤上,指针转过9°. (2)解:因为=3(千克), 所以菜的质量共有3千克. 19.度数 20.顶点 相等 射线 21.D 22.C 23.∠AOD ∠DOA>∠DOB>∠DOC 24.解:∠AOC=∠BOD.理由如下: 因为∠AOB=∠AOC+∠BOC, ∠COD=∠BOD+∠BOC, 而∠AOB=∠COD, 所以∠AOC+∠BOC=∠BOD+∠BOC. 即∠AOC=∠BOD. 25.解:因为OE为∠AOC的角平分线, ∠AOC=120°, 所以∠COE=∠AOC=×120°=60°. 因为OD是∠BOC的角平分线, ∠BOC=30°, 所以∠COD=∠BOC=×30°=15°. 所以∠DOE=∠COE-∠COD=60°-15°=45°. 26.A 27.COB DOB 28.72° 29.(1)解:由图可以看出∠AOB<∠AOC<∠AOD<∠AOE,其中∠AOB为锐角,∠AOC为直角,∠AOD为钝角,∠AOE为平角. (2)解:答案不唯一,如∠AOB+∠BOC=∠AOC,2∠AOC=∠AOE等. 30.解:因为∠AOB=∠BOC, 所以∠AOB=∠AOC, 即∠AOC=3∠AOB. 又因为∠COD=∠AOD=3∠AOB, 所以∠COD=∠AOD=∠AOC. 又因为∠COD+∠AOD+∠AOC=360°, 所以∠COD=∠AOD=∠AOC=120°. 所以∠AOB=×120°=40°. 31.(1)解:因为∠AOC=58°,OD平分∠AOC, 所以∠AOD=29°, 所以∠BOD=180°-29°=151°; (2)解:OE是∠BOC的平分线.理由如下: 因为∠AOC=58°, 所以∠BOC=122°. 因为OD平分∠AOC, 所以∠DOC=×58°=29°. 因为∠DOE=90°, 所以∠COE=90°-29°=61°, 所以∠COE=∠BOC, 所以OE是∠BOC的平分线.查看更多