- 2021-06-21 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年1月崇明中考数学一模试题
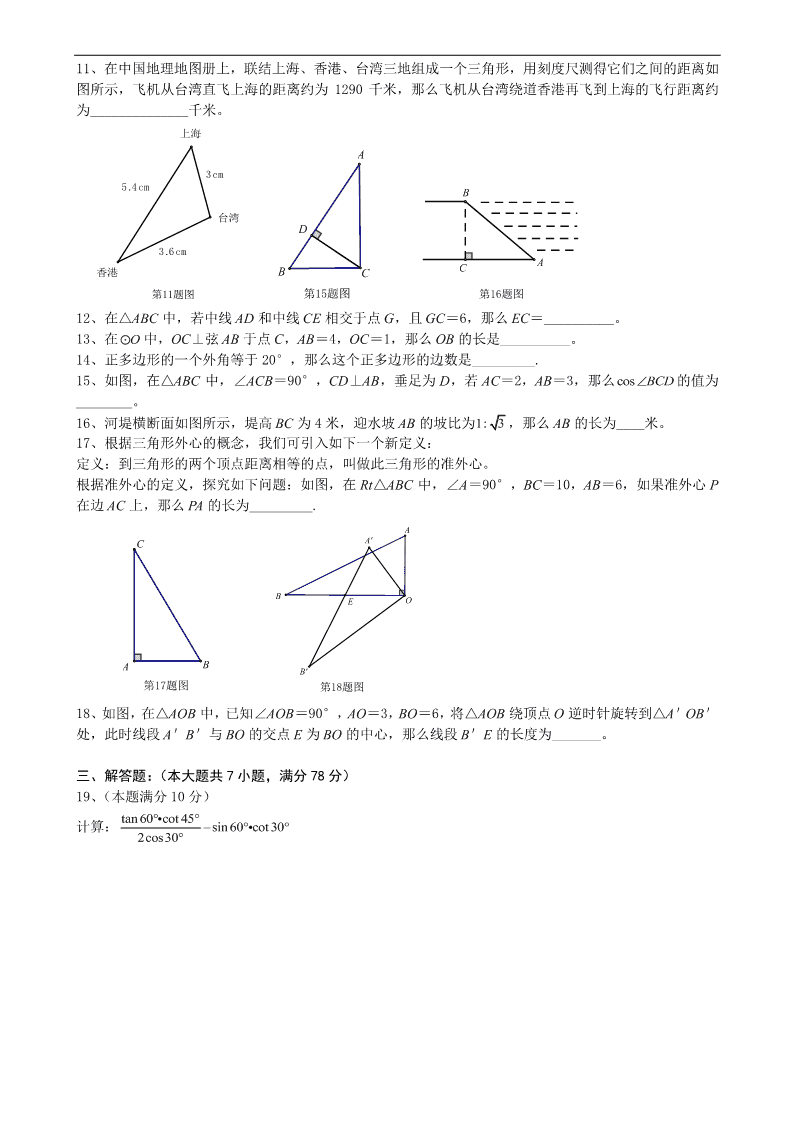
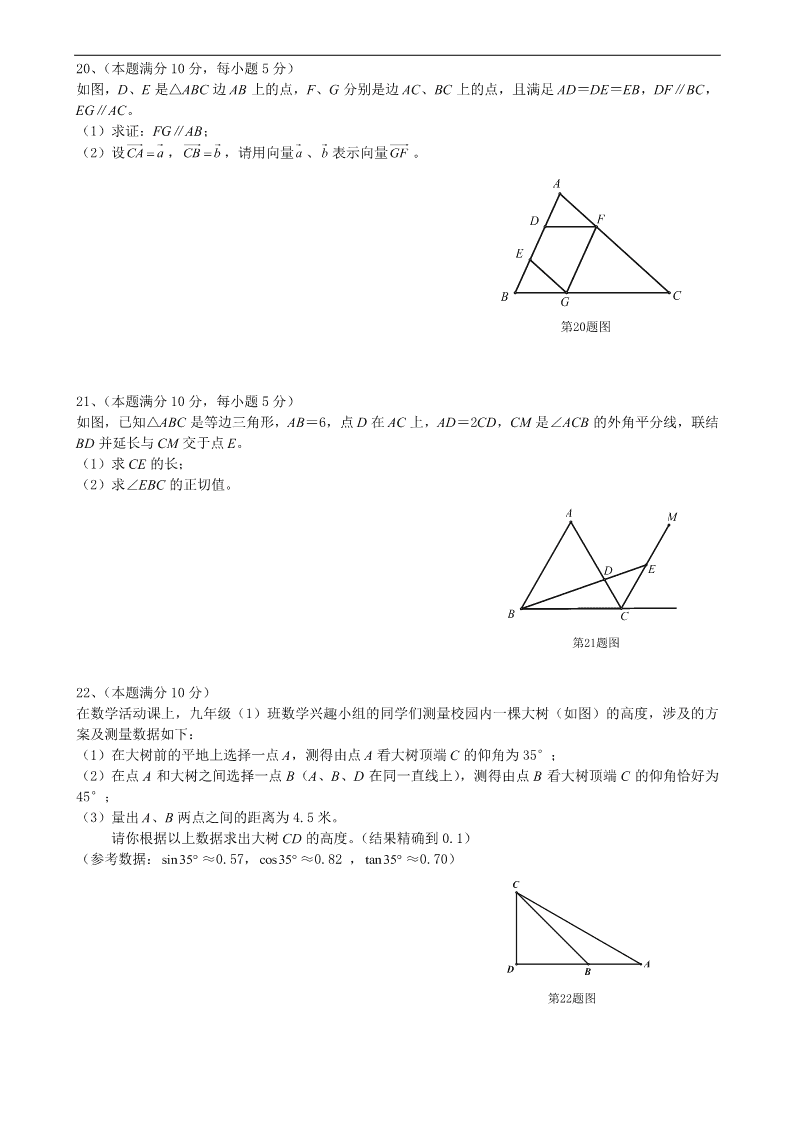
2013~14 学年上海市崇明县初三第一学期期末考试数学试卷 (满分:150 分 考试时间:100 分钟) 考生注意: 1、本试卷含有三个大题,共 25 小题; 2、答题时,考生务必按照答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3、除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步 骤. 一、选择题:(本大题共 6 题,每题 4 分,满分 24 分) 【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确项的代号并填涂在答题纸的相应位置 上】 1、已知 1 2 a b ,那么 a ab 的值是( ) A、 1 2 B、 2 3 C、 1 3 D、 3 4 2、在 Rt△ABC 中,∠C=90°, B ,AB=a,那么 BC 的长为( ) A、 sina B、 cosa C、 cos a D、 tana 3、如果两个相似三角形的面积比为1: 2 ,那么它们的周长比为( ) A、1: 2 B、1: 4 C、1: 2 D、 2:1 4、平面直角坐标系中,将抛物线 22yx 向下平移 2 个单位,那么所得抛物线的解析式为( ) A、 222yx B、 222yx C、 222yx D、 222yx 5、如图,已知 AD∥BC,AC 与 BD 相交于点 O,点 G 是 BD 的中点,过点 G 作 GE∥BC 交 AC 于点 E, 如果 AD=1,BC=3,那么 GE:BC 等于( ) A、1: 2 B、1:3 C、1: 4 D、 2:3 6、如图,点 O 在 A外,点 P 在线段 OA 上运动,以 OP 为半径的 O 与 的位置关系不可能是( ) A、外切 B、相交 C、外离 D、内含 二、填空题:(本大题共 12 题,每小题 4 分,满分 48 分) 7、化简: 3 2 2a b a b _______________. 8、线段 AB=10cm,点 P 是线段 AB 的黄金分割点,且 AP>BP,那么 AP=____________cm。 9、如果抛物线 21 2 3y k x x 的开口向上,那么 k 的取值范围是_____________。 10、抛物线 2 45y x x 的对称轴是直线__________________。 第5题图 O G D B C A E 第6题图 O AP 11、在中国地理地图册上,联结上海、香港、台湾三地组成一个三角形,用刻度尺测得它们之间的距离如 图所示,飞机从台湾直飞上海的距离约为 1290 千米,那么飞机从台湾绕道香港再飞到上海的飞行距离约 为______________千米。 12、在△ABC 中,若中线 AD 和中线 CE 相交于点 G,且 GC=6,那么 EC=__________。 13、在 O 中,OC⊥弦 AB 于点 C,AB=4,OC=1,那么 OB 的长是__________。 14、正多边形的一个外角等于 20°,那么这个正多边形的边数是_________. 15、如图,在△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D,若 AC=2,AB=3,那么cos BCD 的值为 ________。 16、河堤横断面如图所示,堤高 BC 为 4 米,迎水坡 AB 的坡比为1: 3 ,那么 AB 的长为____米。 17、根据三角形外心的概念,我们可引入如下一个新定义: 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。 根据准外心的定义,探究如下问题:如图,在 Rt△ABC 中,∠A=90°,BC=10,AB=6,如果准外心 P 在边 AC 上,那么 PA 的长为_________. 18、如图,在△AOB 中,已知∠AOB=90°,AO=3,BO=6,将△AOB 绕顶点 O 逆时针旋转到△A'OB' 处,此时线段 A'B'与 BO 的交点 E 为 BO 的中心,那么线段 B'E 的长度为_______。 三、解答题:(本大题共 7 小题,满分 78 分) 19、(本题满分 10 分) 计算: tan 60 cot 45 sin 60 cot 302cos30 5.4cm 3.6cm 3cm 香港 台湾 上海 第11题图 第15题图 D C A B 第16题图 C B A 第17题图 A B C 第18题图 E B' O A B A' 20、(本题满分 10 分,每小题 5 分) 如图,D、E 是△ABC 边 AB 上的点,F、G 分别是边 AC、BC 上的点,且满足 AD=DE=EB,DF∥BC, EG∥AC。 (1)求证:FG∥AB; (2)设CA a ,CB b ,请用向量 a 、 b 表示向量GF 。 21、(本题满分 10 分,每小题 5 分) 如图,已知△ABC 是等边三角形,AB=6,点 D 在 AC 上,AD=2CD,CM 是∠ACB 的外角平分线,联结 BD 并延长与 CM 交于点 E。 (1)求 CE 的长; (2)求∠EBC 的正切值。 22、(本题满分 10 分) 在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,涉及的方 案及测量数据如下: (1)在大树前的平地上选择一点 A,测得由点 A 看大树顶端 C 的仰角为 35°; (2)在点 A 和大树之间选择一点 B(A、B、D 在同一直线上),测得由点 B 看大树顶端 C 的仰角恰好为 45°; (3)量出 A、B 两点之间的距离为 4.5 米。 请你根据以上数据求出大树 CD 的高度。(结果精确到 0.1) (参考数据:sin35 ≈0.57, cos35 ≈0.82 , tan35 ≈0.70) 第20题图 G FD E A B C 第21题图 ED B C A M 第22题图 BD A C 23、(本题满分 12 分,其中第 1 小题 5 分,第 2 小题 7 分) 如图,△ABC 中,点 D、E 分别在 BC 和 AC 边上,点 G 是 BE 边上一点,且∠BAD=∠BGD=∠C,联结 AG。 (1)求证: BD BC BG BE ; (2)求证:∠BGA=∠BAC。 24、(本题满分 12 分,每小题各 4 分) 在平面直角坐标系 xOy 中,抛物线 2y x bx c 与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),点 B 的坐 标为 3,0 ,与 y 轴交于点 0,3C ,顶点为 D。 (1)求抛物线的解析式及顶点 D 坐标; (2)联结 AC、BC,求∠ACB 的正切值; (3)点 P 是抛物线的对称轴上一点,当△PBD 与△CAB 相似时,求点 P 坐标。 B CA D E G 25、(本题满分 14 分,其中第 1、2 小题各 5 分,第 3 小题 4 分) 如图,在△ABC 中,AB=8,BC=10, 3cos 4C , 2ABC C ,BD 平分∠ABC 交 AC 边于点 D,点 E 是 BC 边上的一个动点(不与 B、C 重合),F 是 AC 边上一点,且∠AEF=∠ABC,AE 与 BD 相交于点 G。 (1)求证: AB BG CE CF ; (2)设 BE=x,CF=y,求 y 与 x 之间的函数关系式,并写出 x 的取值范围; (3)当△AEF 是以 AE 为腰的等腰三角形时,求 BE 的长。 G F D A B CE 2013~14 学年上海市崇明县初三第一学期期末考试数学试卷参考答案 一、选择题 1、C 2、B 3、C 4、A 5、B 6、D 二、填空题 7、 4a+ b 8、5 5 5 9、 1k 10、 2x 11、3870 12、 9 13、 5 14、18 15、 2 3 16、8 17、4 或 7 4 18、 95 5 三、解答题 19、解:原式 3 1 3 3 1312 2 232 2 20、( 1)证明:∵ AD DE EB ∴ 11 33 AD BE AB AB ∵DF∥BC,EG∥AC ∴ 1 3 AF AD AC AB, 1 3 BG BE BC AB ∴ AF BG AC BC ∴FG∥AB (2)解:∵DF∥BC ∴ 2 3 CF BD AC BA ∵GF∥AB ∴ 2 3 FG CF AB AC ∴ 2 3FG AB ∵ GF 与 BA 同向 ∴ 2 3GF BA ∵ CA a ,CB b ∴ BA a b ∴ 22 33GF a b 21、( 1)解:在 BC 延长线上取一点 F,∵△ABC 是等边三角形 ∴ 60ABC ACB , 6AB AC, 120ACF ∵CM 是 ACB 的外角平分线 ∴ 1 602ECF ACF ∴ ECF ABC ∴CE∥AB ∴ CE CD AB AD 又∵ 2AD CD , 6AB ∴ 1 62 CE ∴ 3CE (2)过点 E 作 EH BC ,垂足为 H ∵ 60ECF , 90EHC , 3CE ∴ 3 2CH , 33 2EH 又∵ 6BC , ∴ 15 2BH BC CH ∵ 90EHB ∴ 3tan 5 EHEBC BH 22、解:由题意得, 35A , 45CBD , 90CDB , 4.5AB 米 设 CD 的长为 x 米, 在 Rt△CDB 中, tan 1CDCBD DB ∴ BD CD x 在 Rt△CDA 中, tan 0.7CDA AD ∴ 0.7CD AD ∴ 0.7 4.5xx ∴ 10.5x 答:大树 CD 的高为10.5 米。 23、( 1)证明:∵ BDG EBC BGD C ∴△BDG∽△BEC ∴ BD BG BE BC ∴ BD BC BG BE (2)证明:∵ DBA ABC , BAD C ∴△DBA∽△ABC ∴ BD AB AB BC ∴ 2AB BD BC ∵ ∴ 2AB BG BE ∴ BG AB AB BE ∵ GBA ABE ∴△GBA∽△ABE ∴ BGA BAC 24、( 1)抛物线 2y x bx c 过点 3,0B , 0,3C ∴ 9 3 0 3 bc c ∴ 4 3 b c ∴ 2 43y x x ∴顶点 D 的坐标为 2, 1 (2)∵抛物线 2 43y x x 与 x 轴交于点 A、B(A 在 B 的左侧) ∴ 1,0A 又∵ 0,0O , 0,3C , 3,0B ∴ 3BO CO ∵ 90COB ∴ 45 , 3 2OBC BC 过点 A 作 AH BC ,垂足为 H,∴ 90AHB ∵ 2AB ∴ 2AH BH ∴ 22CH BC BH ∴ 21tan 222 AHACB CH (3)∵抛物线 2 43y x x 的对称轴为直线 2x 点 P 是抛物线对称轴上一点, ∴可设点 P 的坐标为 2,n 把对称轴直线 与 x 轴的交点记为 E,则点 E 的坐标为 2,0 ∵ 2, 1D , 3,0B ∴ 1, 2DE BE BD ∵ 90BED ∴ 45EDB EBD ∴ 45CBO BDE ∴当△PBD 与△CAB 相似时,点 P 在点 D 的上方,并存在以下两种情况: 1° BD BA DP BC ∴ 22 1 32n ∴ 2n ∴ 2,2P 2° BD BC DP BA ∴ 2 3 2 12n ∴ 1 3n ∴ 12, 3P 综上所述,当△PBD 与△CAB 相似时,点 或 。 25、( 1)证明:∵BD 平分 ABC ∴ 2ABC ABD ∵ 2ABC C ∴ ABD C ∵ AEC ABC BAE 即 AEF FEC ABC BAE ∵ AEF ABC ∴ BAE FEC ∴△ABG∽△ECF ∴ AB BG CE CF (2)过点 A 作 BC 的平行线交 BD 的延长线于点 M ∵AM∥BC ∴∠M=∠DBC ∵∠ABD=∠DBC ∴∠M=∠ABD ∴AM=AB=8 过点 A 作 AN MB ,垂足为 N ∵ 3,cos ,4ABD C C AB AC ∴ 6, 12BN MN BM ∵AM∥BC ∴ AM MG BE BG ∴ 8 12 BG x BG ∴ 12 8 xBG x ∵ AB BG CE CF ∴ 12 8 8 10 x x xy ∴ 230 3 0 102 16 xxyxx (3)当△AEF 是以 AE 为腰的等腰三角形时存在以下两种情况: 1° AE AF ,则 AEF AFE 易证明 FE FC y, 又∵ 3cos 4C 易得 3 2EC y , 又∵ 10EC x ∴ 20 2 3 xy 又∵ 230 3 2 16 xxy x 解得 126.4 , 10xx舍去 即 BE 的长为 6.4 2° EA EF 作线段 CF 的垂直平分线交 BC 于点 H,交 FC 于点 K,联结 HF 则易证△ABE≌△EHF,HF=HC ∴ 8,AB EH BE FH HC x ∴ 2 8 10x ∴ 1x 即 BE 的长为 1 综上所述,当△AEF 是以 AE 为腰的等腰三角形时,BE 的长为 6.4 或 1。查看更多