- 2021-06-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2009年福建省福州市中考试题及答案
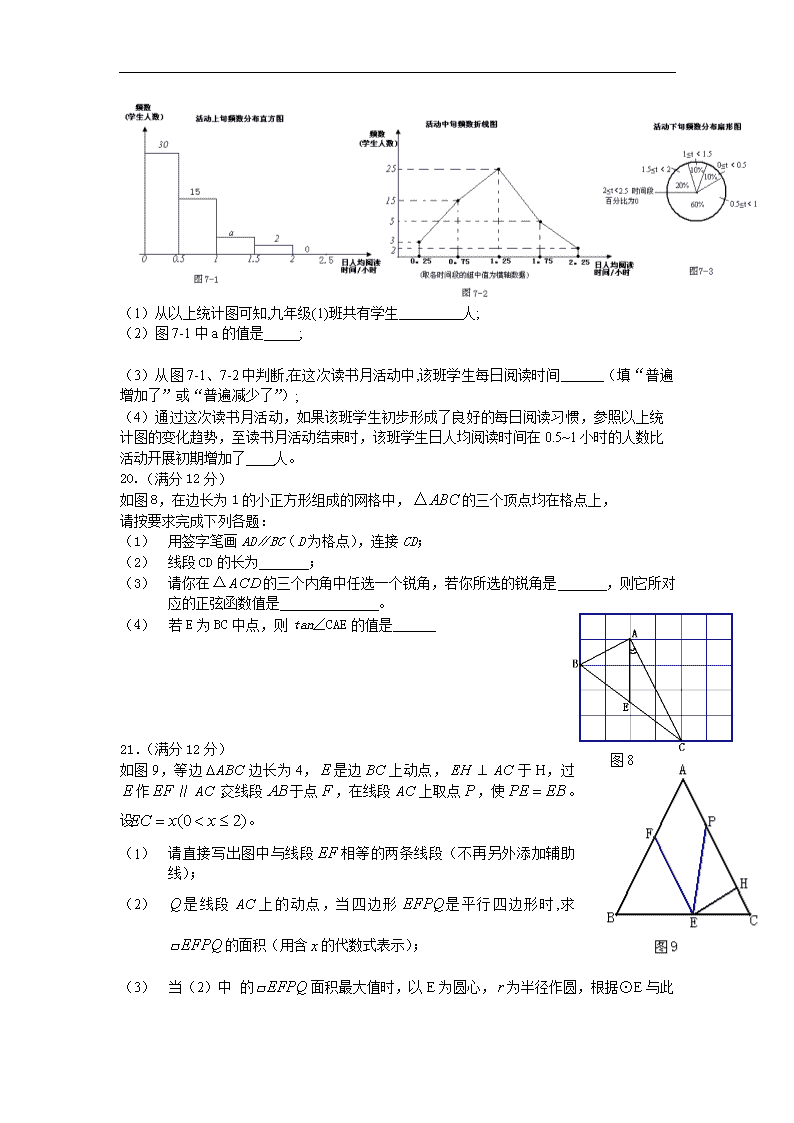
二○○九年福州市课改实验区初中毕业会考、高级中等学校招生考试 数 学 试 卷 (全卷共4页,三大题,共22小题;满分150分;考试时间120分钟) 友情提示:所有答案都必须填涂在答题卡上,答在本试卷上无效. 毕业学校 姓名 考生号 一、选择题(共10小题,每题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂) 1.2009的相反数是 A.-2009 B.2009 C. D. 2.用科学记数法表示660 000的结果是 A.66×104 B.6.6×105 C.0.66×106 D.6.6×106 3.已知∠1=30°,则∠1的余角度数是 A.160° B.150° C.70° D.60° 4.二元一次方程组的解是 A. B. C. D. 5. 图1所示的几何体的主视图是 A. B. C. D. 图1 图2 6.下列运算中,正确的是 A.x+x=2x B. 2x-x=1 C.(x3)3=x6 D. x8÷x2=x4 7.若分式有意义,则x的取值范围是 A.x≠1 B.x>1 C. x=1 D.x<1 8.如图2,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是 A.2DE=3MN, B.3DE=2MN, C. 3∠A=2∠F D.2∠A=3∠F 图3 9.将1、2、3三个数字随机生成的点的坐标,列成下表。如果每个点出现的可能性相等,那么从中任意取一点,则这个点在函数y=x图象上的概率是 (1,1) (1,2) (1,3) (2,1) (2,2) (2,3) (3,1) (3,2) (3,3) A.0.3 B.0.5 C. D. 10.如图3, 是以等边三角形ABC一边AB为半径的四分之一圆周, P为 上任意一点,若AC=5,则四边形ACBP周长的最大值是 A. 15 B. 20 C.15+ D.15+ 图5 二、填空题(共5小题,每题4分,满分20分.请将答案填入答题卡的相应位置) 11.分解因式:= 12.请写出一个比小的整数 13. 已知,则的值是 14. 如图4,AB是⊙O的直径,点C在⊙O上 ,OD∥AC,若BD=1,则BC的长为 图6 15.已知, A、B、C、D、E是反比例函数(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示) 三、解答题(满分90分.请将答案填入答题卡的相应位置) 16.(每小题7分,共14分) (1)计算:22-5×+ (2)化简:(x-y)(x+y)+(x-y)+(x+y) 17.(每小题8分,共16分) (1)解不等式:,并在数轴上表示解集. (2)整理一批图书,如果由一个人单独做要花60小时。现先由一部分人用一小时整理,随后增加15人和他们一起又做了两小时,恰好完成整理工作。假设每个人的工作效率相同,那么先安排整理的人员有多少人? 18.(满分10分) 如图6,已知AC平分∠BAD,∠1=∠2,求证:AB=AD 19.(满分12分)以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况: (1)从以上统计图可知,九年级(1)班共有学生 人; (2)图7-1中a的值是 ; (3)从图7-1、7-2中判断,在这次读书月活动中,该班学生每日阅读时间 (填“普遍增加了”或“普遍减少了”); (4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了 人。 20.(满分12分) 如图8,在边长为1的小正方形组成的网格中,的三个顶点均在格点上, 请按要求完成下列各题: (1) 用签字笔画AD∥BC(D为格点),连接CD; (2) 线段CD的长为 ; 图8 (3) 请你在的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 。 (4) 若E为BC中点,则tan∠CAE的值是 21.(满分12分) 如图9,等边边长为4,是边上动点,于H,过作∥,交线段于点,在线段上取点,使。设。 (1) 请直接写出图中与线段相等的两条线段(不再另外添加辅助线); (2) 是线段上的动点,当四边形是平行四边形时,求 的面积(用含的代数式表示); (3) 当(2)中 的面积最大值时,以E为圆心,为半径作圆,根据⊙E与 此时四条边交点的总个数,求相应的的取值范围。 图10 22.(满分14分) 已知直线l:y=-x+m(m≠0)交x轴、y轴于A、B两点,点C、M分别在 线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M 旋转180°,得到△FEM,则点E在y轴上, 点F在直线l上;取线段EO中 点N,将ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记: 过点F的双曲线为,过点M且以B为顶点的抛物线为,过点P且以M 为顶点的抛物线为. (1) 如图10,当m=6时,①直接写出点M、F的坐标, ②求、的函数解析式; (2)当m发生变化时, ①在的每一支上,y随x的增大如何变化?请说明理由。 ②若、中的y都随着x的增大而减小,写出x的取值范围。 二○○九年福州市课改实验区初中毕业会考、高级中等学校招生考试 数学试卷参考答案 一、选择题(每小题4分,共40分) 1.A 2.B 3.D 4.C 5.D 6.A 7.A 8.B 9.C 10.C 二、填空题(每小题4分,共20分) 11.x(x-2) 12.答案不唯一,小于或等于2的整数均可,如:2,1等 13.5 14.2 15.13π-26 三、解答题 16.(1)解:原式=4-1+2 =3+2 =5.……………………7分 (2)解:原式= =.……………………7分 17.(1)解:3x-x>2 2x>2 x>1.……………………6分 ……………………8分 (2)解:设先安排整理的人员有x人,依题意得, ……………………4分 解得, x=10. 答:先安排整理的人员有10人.……………………8分 图6 18.证明:∵AC平分∠BAD ∴∠BAC=∠DAC. ∵∠1=∠2 ∴∠ABC=∠ADC. 在△ABC和△ADC中 ∴△ABC≌△ADC(AAS).……………………8分 ∴AB=AD.……………………10分 (其他不同证法,参照以上标准评分) 19.(每小题各3分,共12分) (1)50 (2)3 (3)普遍增加了 (4)15 20.(每小题3分,共12分) (1)如图 (2) (3)∠CAD,(或∠ADC,) (4) 21.解:(1)BE、PE、BF三条线段中任选两条.………………………2分 (2)在Rt△CHE中,∠CHE=90° ∠C=60°, ∴EH= ∵PQ=EF=BE=4-x ∴.……………………5分 (3) ∴当x=2时,有最大值. 此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、 点Q重合 ∴平行四边形EFPQ是菱形. 过E点作ED⊥FP于D, ∴ED=EH=. ∴当⊙E与四条边交点的总个数是2个时,0<r<; 当⊙E与四条边交点的总个数是4个时,r=; 当⊙E与四条边交点的总个数是6个时,<r<2; 当⊙E与四条边交点的总个数是3个时,r=2时; 当⊙E与四条边交点的总个数是0个时,r>2时. …………………………………………………………12分 22.解:(1)①点M的坐标为(2,4),点F的坐标为(-2,8).……………………2分 ② 设的函数解析式为(. ∵过点F(-2,8) ∴的函数解析式为. ∵的顶点B的坐标是(0,6) ∴设的函数解析式为. ∵过点M(2,4) ∴ . ∴的函数解析式为.……………………6分 (2)依题意得,A(m,0),B(0,m), ∴点M坐标为(),点F坐标为(,). ①设的函数解析式为(. ∵过点F(,) ∴. ∵ ∴ ∴在的每一支上,y随着x的增大而增大. ②答:当>0时,满足题意的x的取值范围为 0<x<; 当<0时,满足题意的x的取值范围为<x<0. ……………………………………………………14分查看更多